Álgebra linear/Imprimir

Capa

Álgebra linear

Wikilivros

"Livros abertos por um mundo aberto"

Créditos

Wikilivristas que participaram do desenvolvimento e manutenção deste wikilivro:

• Albmont
• Dante
• Edudobay
• Felipe.sanches
• Helder
• João Jerónimo
• Jorge Morais
• LeonardoG
• Marcos Antônio Nunes de Moura
• Master
• Ozymandias
• Petrusz1
• Rodrigo Rocha
• Thiagoharry
• Thiago Marcel

Introdução

Bem-vindo ao mundo da Álgebra Linear! Este livro foi escrito para ajudá-lo a compreender as complexidades e os conceitos fundamentais dessa área da matemática. Desde o estudo de sistemas de equações lineares até a análise de transformações lineares e diagonalização de matrizes, este livro irá guiá-lo em sua jornada de aprendizado de Álgebra Linear.

Com suas muitas aplicações em campos como matemática, ciência da computação, engenharia e física, a Álgebra Linear é uma das áreas mais importantes e úteis da matemática. Neste livro, você terá a oportunidade de explorar os conceitos fundamentais da Álgebra Linear de uma forma abrangente e detalhada. Ao longo das páginas, você aprenderá sobre espaços vetoriais, sistemas de equações lineares, determinantes, valores e vetores próprios, produtos internos e externos, e muitos outros tópicos. Cada capítulo contém explicações claras e concisas, exemplos ilustrativos e exercícios práticos para ajudá-lo a entender e praticar os conceitos.

Este livro apresenta uma abordagem didática e abrangente, com exemplos ilustrativos, exercícios e problemas práticos, além de explanações claras e concisas. Esperamos que, ao final da leitura, você tenha uma sólida compreensão dos conceitos e uma base sólida para prosseguir em sua jornada de estudos matemáticos. Boa leitura!

Sistemas de equações lineares

Este estudo de álgebra linear começará com a análise dos sistemas de equações lineares. Tais sistemas aparecem frequentemente em matemática aplicada, economia e engenharia ao modelar certos fenômenos. Por exemplo, em programação linear, geralmente é discutido como maximizar o lucro quando existem certas restrições relacionadas a dificuldade, disponibilidade de tempo, ou outras condições. Estas restrições podem ser colocadas na forma de um sistema de equações lineares.

Equações lineares

Uma equação linear é uma equação composta exclusivamente de adições e subtrações de termos que são constantes ou o produto de uma constante pela primeira potência de uma variável.

Conforme a natureza do problema que dá origem a equação, as constantes e as variáveis podem ser números inteiros, reais, complexos ou ter uma estrutura ainda mais geral (veja, por exemplo, um artigo sobre "corpos" na Wikipédia). No caso dos números inteiros, chama-se a equação de "equação linear diofantina", e seu estudo é feito na teoria de números.

Neste Wikilivro, será considerado que as constantes e as variáveis de uma equação linear são elementos de um subcorpo $F$ do corpo dos números complexos. Os elementos de $F$ serão chamados de escalares. Para a maior parte do texto, o leitor não familiarizado com corpos e outras estruturas algébricas pode admitir que os escalares são os números complexos.

Uma caracterização mais formal do que se entende por "equação linear" é a seguinte:

Definição

Uma equação linear em $n$ variáveis sobre o corpo $F$ é uma equação que pode ser colocada na forma $a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}+\ldots +a_{n}x_{n}=b$, sendo que os escalares $a_{1},a_{2},\ldots ,a_{n}$ são denominados coeficientes, e $b$ é chamado de termo independente, ou termo constante.

Cada equação linear pode ser vista como uma igualdade entre zero e um polinômio do primeiro grau em várias variáveis, uma vez que:

$a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}+\ldots +a_{n}x_{n}=b\ \Leftrightarrow$$\ a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}+\ldots +a_{n}x_{n}-b\ =\ 0$

Como foi ressaltado no exemplo, para uma equação ser chamada de "linear", ela não precisa necessariamente estar com todas as variáveis no membro esquerdo da equação, embora seja usual escrevê-la assim. Como será visto posteriormente, usando essa convenção é possível simplificar a resolução de sistemas de equações lineares (veja adiante), introduzindo o conceito de matriz.

Soluções de uma equação linear

Definição

Uma solução da equação linear $a_{1}x_{1}+a_{2}x_{2}+a_{3}x_{3}+\ldots +a_{n}x_{n}=b$ é uma $n$-upla (um vetor) $s=(s_{1},s_{2},\ldots s_{n})$, cujas entradas $s_{j}$ podem ser colocadas no lugar de cada $x_{j}$, para $j=1,\ldots ,n$, de modo que a igualdade seja verdadeira. O conjunto solução de uma equação linear é aquele formado por todas as suas soluções.

Por exemplo, $(-1,-1)$ é uma solução da equação linear $x+3y=-4$, uma vez que $(-1)+3\times (-1)=-1+(-3)=-4$, mas $(1,5)$ não.

No caso em que a quantidade de variáveis em uma equação linear é menor ou igual a três, pode-se associar ao seu conjunto solução, uma interpretação geométrica. Acompanhe os exemplos a seguir:

Representação gráfica de duas equações lineares

Pode-se generalizar a relação entre equações lineares e geometria para o caso em se tem um número arbitrário de variáveis. No entanto, nessa situação não é possível visualizar a "forma geométrica" que corresponde às soluções da equação. O termo utilizado para descrever a forma geométrica correspondente ao conjunto solução de uma equação a $n$ variáveis é hiperplano afim, de dimensão $n$. Neste texto, no entanto, será usado simplesmente a terminologia $n$-plano.

Sistemas de equações lineares

Definição

Um sistema de equações lineares (ou sistema linear) é uma coleção de equações lineares envolvendo o mesmo conjunto de variáveis.

Um sistema geral de $m$ equações lineares com $n$ incógnitas (ou variáveis) pode ser escrito como

$\left\{{\begin{matrix}a_{11}x_{1}+a_{12}x_{2}+\cdots +a_{1n}x_{n}=b_{1}\\a_{21}x_{1}+a_{22}x_{2}+\cdots +a_{2n}x_{n}=b_{2}\\\vdots \\a_{m1}x_{1}+a_{m2}x_{2}+\cdots +a_{mn}x_{n}=b_{m}\\\end{matrix}}\right.$

Aqui, $x_{1},\ x_{2},...,x_{n}$ são as incógnitas, $a_{11},\ a_{12},...,\ a_{mn}$ são os coeficientes do sistema, e $b_{1},\ b_{2},...,b_{m}$ são os termos constantes.

A "chave" colocada à esquerda das equações é uma forma de lembrar que todas as equações devem ser consideradas em conjunto. A seguir são apresentados alguns exemplos de equações lineares.

Soluções de sistemas lineares

Definição

Uma solução de um sistema linear é uma $n$-upla de valores $s=(s_{1},s_{2},....,s_{n})$ que simultâneamente satisfazem todas as equações do sistema.

Cada equação de um sistema linear em três variáveis determina um plano. Uma solução do sistema corresponde a um ponto na interseção desses planos

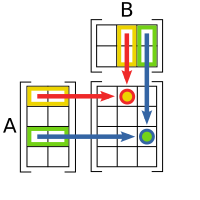
A coleção de todas as possíveis soluções de um sistema linear será chamada de conjunto solução, sendo geralmente denotado por $S$. Uma fórmula que descreva todos os vetores do conjunto solução é chamada de solução geral. Dessa definição, decorre que o conjunto solução de um sistema linear é a interseção entre os conjuntos soluções de cada equação do sistema (veja a figura).

Um sistema linear é dito consistente se possui alguma solução. Caso contrário, é chamado de inconsistente.

Em geral, para qualquer sistema linear existem três possibilidades a respeito das soluções:

• Uma única solução: Neste caso, existe apenas uma solução específica (uma certa $n$-upla). O conjunto $S$ tem um único elemento. Geometricamente, isto implica que os $n$-planos determinados pelas equações do sistema se intersectam todos em um mesmo ponto do espaço, que é especificado pelas coordenadas da solução (as "entradas" da $n$-upla). O sistema é dito possível (existe alguma solução) e determinado (existe uma única solução);
• Nenhuma solução: Nesta situação, não existe qualquer $n$-upla de valores que verifiquem simultaneamente todas as equações do sistema. O conjunto $S$ é vazio. Geometricamente, os $n$-planos correspondentes as equações não se intersectam (são paralelos). O sistema é dito impossível (não existe solução).
• Infinitas soluções: As equações especificam $n$-planos cuja intersecção é um $m$-plano onde $m\leq n$. Sendo este o caso, é possível explicitar um conjunto $S$ com infinitas soluções. O sistema é dito possível (existe alguma solução) e indeterminado (sua quantidade é infinita)

As seguintes figuras ilustram os casos acima:

Uma única solução	Nenhuma solução	Infinitas soluções

Sistemas lineares equivalentes

Definição

Dois sistemas lineares são ditos equivalentes quando possuem o mesmo conjunto solução.

Nos exemplos anteriores, pode-se notar que todos os sistemas possuem o mesmo conjunto solução (são equivalentes), embora no exemplo (V) a solução não esteja "tão evidente" como no caso de (I).

Isso sugere uma estratégia para resolver sistemas lineares: para determinar o conjunto solução de um sistema linear arbitrário (por exemplo (V)), basta encontrar um outro sistema linear que lhe seja equivalente, mas cuja solução seja imediata (como o (I), cuja solução é óbvia!).

Resta agora encontrar uma forma de produzir sistemas lineares equivalentes a um sistema dado, e que sejam simples (senão imediatos!) de resolver. As técnicas usadas para este fim serão apresentadas na próxima seção.

Operações com equações

Para um melhor entendimento das técnicas que podem ser utilizadas na resolução de sistemas lineares, serão sintetizadas no teorema a seguir as "operações" que podem ser feitas com as equações de um sistema, sem que seu conjunto solução seja alterado. Como será visto posteriormente, é possível determinar o conjunto solução de qualquer sistema linear (resolver o sistema), usando apenas três "operações elementares".

Teorema

Se um sistema linear é obtido a partir de outro, através de uma dessas operações

1. Trocar a posição de duas equações;
2. Trocar uma equação por um múltiplo (não nulo) de si mesma;
3. Trocar uma equação pela soma de si mesma com um múltiplo de outra equação;

então ele possui as mesmas soluções que o sistema original.

Demonstração

• Deixada a cargo do leitor. Sinta-se a vontade para acrescentá-la ao texto.

Métodos para a resolução de sistemas lineares

Eliminação de variáveis

Um método bastante simples para a resolução de um sistema linear é eliminar as variáveis, uma após a outra. Este método consiste dos seguintes passos:

1. Na primeira equação, isole uma das variáveis em função das outras.
2. Substitua a expressão acima em cada uma das outras equações. Isso produz um outro sistema de equações, com uma equação a menos e uma variável a menos.
3. Repita o passo anterior até que reste apenas uma equação linear.
4. Resolva esta equação e use a resposta obtida para determinar as demais variáveis nas outras equações.

Sabe-se que sistemas lineares em poucas variáveis também podem ser resolvidos usando outros métodos.

Observe, no entanto, que estas técnicas não são muito práticas ao lidar com sistemas grandes, onde exista um grande número de variáveis. Apesar disso, tais procedimentos podem ser generalizados, dando origem a algoritmos como a eliminação de Gauss e a eliminação de Gauss-Jordan, que pode ser usado em situações bem mais gerais.

O método da eliminação gaussiana será estudado em um capítulo posterior.

Muitas vezes é preciso resolver vários sistemas lineares que diferem apenas em seus termos constantes. Os coeficientes das incógnitas permanecem os mesmos. Uma técnica chamada de decomposição LU é usada nestes casos. Em situações muito particulares, ela adminte uma variante conhecida como fatoração de Cholesky. Tais técnicas serão estudadas nos últimos capítulos.

Exercícios

Este capítulo é apenas uma revisão. Não há exercícios.

Esta página foi eleita pelos colaboradores como uma das melhores do Wikilivros. Para mais informações, consulte a página de votações.

Matrizes

A distribuição do conteúdo deste livro está confusa ou pouco didática (discuta). Pede-se aos editores que reavaliem a distribuição do mesmo.

Este módulo tem a seguinte tarefa pendente: É preciso fixar a notação para as entradas das matrizes ao longo do livro, pois ora são usadas $a_{ij}$ e ora $A_{ij}$ para as entradas de uma matriz $A$.

Introdução

O termo matriz pode ser mais conhecido entre programadores e profissionais da informática, como sendo uma estrutura de dados. Em matemática, no entanto, matrizes são consideradas de forma bastante diferente.

Definição

Intuitivamente, uma matriz é uma lista de números, dispostos em linhas e colunas, ou seja, é um tipo de tabela.

Logo abaixo, apresenta-se uma matriz. A notação utilizada é bastante comum.

$A={\begin{pmatrix}2&4&10\\1&-3&-7\\3&0&0\\5&5&0\end{pmatrix}}$

A matriz acima tem 4 linhas e 3 colunas, então pode ser chamada de matriz 4 × 3 (matriz 4 por 3). Além disso, pode-se ter matrizes de muitas formas diferentes. A forma de uma matriz é o nome das dimensões da mesma (m por n, quando m é o número de linhas e n é o número de colunas). A seguir são indicados alguns outros exemplos de matrizes, adotando outras possíveis notações.

Este é um exemplo de matriz 3 × 3:

$B={\begin{pmatrix}1&2&3\\4&5&6\\7&8&9\\\end{pmatrix}}$

Esta matriz tem a forma 5 × 4:

$T={\begin{pmatrix}a&b&c&d\\h&g&f&e\\i&j&k&l\\p&o&n&m\\q&r&s&t\\\end{pmatrix}}$

Aqui, tem-se uma matriz 1 × 6:

$V={\begin{pmatrix}2&3&5&7&11&13\\\end{pmatrix}}$

As matrizes são objetos matemáticos que além de permitirem uma boa organização espacial de conjuntos de dados numéricos, podem ser operadas com números (multiplicação por escalar) e com outras matrizes (sendo adicionadas, multiplicadas, etc). Entender as operações sobre matrizes é essencial para o aprendizado de Álgebra Linear.

Uma matriz é formada por linhas, que são conjuntos de dados dispostos horizontalmente e por colunas, conjuntos de dados dispostos verticalmente. Cada elemento presente em uma matriz é indicado por uma letra minúscula que possui como índice um par ordenado que representa o número da linha e o da coluna. Costuma-se representar total de linhas de uma matriz pela letra m e o número total de colunas por n. Os valores de m e de n são as dimensões da matriz.

Organização de uma matriz

Exemplos de matrizes

A matriz a seguir é uma matriz de ordem 2×3 com elementos naturais.

$A={\begin{bmatrix}1&2&3\\4&5&6\end{bmatrix}}$

Nesse exemplo, o elemento $a_{12}$ é 2, o número na primeira linha e segunda coluna do quadro.

De forma geral, numa matriz A de ordem m × n, o elemento $a_{ij}$ é o símbolo na i-ésima linha e j-ésima coluna de A. Assim:.

$A={\begin{bmatrix}a_{11}&a_{12}&\cdots &a_{1n}\\a_{21}&a_{22}&\cdots &a_{2n}\\\vdots &\vdots &\ddots &\vdots \\a_{m1}&a_{m2}&\cdots &a_{mn}\end{bmatrix}}$

As entradas (símbolos) de uma matriz também podem ser definidas de acordo com seus índices i e j. Por exemplo, $a_{ij}=i+j,$ para $i$ de 1 a 3 e $j$ de 1 a 2, define a matriz 3×2 $A={\begin{bmatrix}2&3\\3&4\\4&5\end{bmatrix}}.$

Abaixo, vemos o exemplo de uma Matriz Quadrada:

$A={\begin{bmatrix}3&5&23\\3&4&5\\4&1&9\end{bmatrix}}$

E agora um exemplo de uma Matriz Identidade:

$A={\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}$

Abaixo seguem informações sobre as principais operações definidas para matrizes. Abaixo matrizes serão representadas por letras maiúsculas e seus índices por letras minúsculas. Números escalares serão representados pela letra $k.$

Tipos especiais de matrizes

• Uma Matriz Quadrada é toda aquela na qual $m=n.$ Isto é, ela possui o mesmo número de linhas e de colunas.
• Uma Matriz Linha é toda aquela na qual $m=1.$ Isto é, ela possui apenas uma linha.
• Uma Matriz Coluna é toda aquela na qual $n=1.$ Isto é, ela possui apenas uma coluna.
• Uma Matriz Diagonal é toda aquela na qual $m=n$ e cujo elemento $A_{i,j}=0$ se $i\neq j.$ Isto é, possui todos os valores iguais à zero, exceto os elementos da diagonal principal.
• Uma Matriz Escalar é toda aquela na qual $m=n$ cujo elemento $A_{i,j}=0$ se $i\neq j$ e $A_{i,j}=X.$ Isto é, todos os valores são nulos, exceto os valores da diagonal principal que possuem sempre o mesmo valor.
• Uma Matriz Nula é toda aquela cujos elementos $A_{i,j}=0.$ Isto é, se todos os seus elementos forem nulos.
• Uma Matriz Identidade é toda aquela na qual $m=n$ cujos elementos $A_{i,j}=0$ se $i\neq j$ e $A_{i,j}=1$ se $i=j.$ Isto é, possui todos os valores nulos, exceto os valores da diagonal principal que valem sempre 1.

Álgebra matricial

Multiplicação por um escalar

A multiplicação por um escalar é uma das operações mais simples que podem ser feitas com matrizes.

Definição

Para multiplicar um número $k$ qualquer por uma matriz m×n $A,$ basta multiplicar cada entrada $a_{ij}$ de $A$ por $k.$ Assim, a matriz resultante $B$ será também m×n e $b_{ij}=k\cdot a_{ij}.$

Com isso, pode-se pensar também na noção de dividir uma matriz por um número: basta multiplicá-la pelo inverso desse número. Mas essa noção pode ser perigosa: enquanto a multiplicação entre um número e uma matriz pode ser dita "comutativa", o mesmo não vale para a divisão, pois não se pode dividir um número por uma matriz.

É impossível somar ou subtrair escalares de matrizes.

A multiplicação por escalar possui as seguintes propriedades:

• Associativa em relação ao Escalar: $(k_{1}\cdot k_{2})\cdot A=k_{1}\cdot (k_{2}\cdot A)$
• Distributiva em relação ao Escalar: $(k_{1}+k_{2})\cdot A=k_{1}\cdot A+k_{2}\cdot A$
• Distributiva em relação à Matriz: $k_{1}\cdot (A+B)=k_{1}\cdot A+k_{1}\cdot B$
• Elemento Neutro: $1\cdot A=A$

Adição de Matrizes

A adição de matrizes é outra operação bastante simples.

Definição

Sempre que uma matriz A é somada à uma matriz B, o resultado será uma matriz C, cujos elementos $c_{ij}=a_{ij}+b_{ij}.$

Perceba que a operação de soma para matrizes de diferentes dimensões não é definida.

A adição de matrizes possui as seguintes propriedades:

• Propriedade Associativa: $A+(B+C)=(A+B)+C$
• Elemento Neutro: $A+0=0+A=A$ ($0$ é uma Matriz Nula, não um escalar)
• Simétrico Aditivo: $-A+A=A-A=0$
• Comutatividade: $A+B=B+A$

Multiplicação de Matrizes

A multiplicação de duas matrizes é bem definida apenas se o número de colunas da matriz da esquerda é o mesmo número de linhas da matriz da direita.

Definição

Se $A$ é uma matriz $m\times n$ e $B$ é uma matriz $n\times p,$ então seu produto $AB$ é a matriz $m\times p$ (m linhas e p colunas) dada por:

$(AB)_{i,j}=a_{i,1}b_{1,j}+a_{i,2}b_{2,j}+\cdots +a_{i,n}b_{n,j}\!\$ para cada par $(i,j).$

A motivação dessa definição é a seguinte: se $\beta _{i}$ denota a $i$-ésima linha da matriz $B,$ podemos criar outra matriz $C$ cujas linhas $\gamma _{1},\ldots ,\gamma _{m}$ sejam combinações lineares das linhas de $B:$

$\gamma _{1}=A_{1,1}\beta _{1}+A_{1,2}\beta _{2}+\cdots +A_{1,n}\beta _{n}$

$\vdots$

$\gamma _{m}=A_{m,1}\beta _{1}+A_{m,2}\beta _{2}+\cdots +A_{m,n}\beta _{n}$

Em cada linha $\gamma _{i},$ a entrada na $j$-ésima coluna será uma combinação linear de todas as entradas de $B$ nessa mesma coluna:

$(\gamma _{i})_{j}=A_{i,1}(\beta _{1})_{j}+A_{i,2}(\beta _{2})_{j}+\cdots +A_{i,n}(\beta _{n})_{j},$

mas $(\beta _{i})_{j}$ corresponde a $B_{i,j}.$ Então, se $A$ for a matriz com as entradas $A_{i,j}$ definidas como acima, obtemos a fórmula acima.

Da mesma maneira, se $\alpha _{j}$ denota a $j$-ésima coluna da matriz $A,$ podemos criar uma matriz $C$ cujas colunas $\gamma _{1},\ldots ,\gamma _{p}$ sejam combinações lineares das colunas de $A:$

$\gamma _{j}=B_{1,j}\alpha _{1}+B_{2,j}\alpha _{2}+\cdots +B_{n,j}\alpha _{n}$

E, tomando as entradas na $i$-ésima linha, obtemos

$(\gamma _{j})_{i}=B_{1,j}(\alpha _{1})_{i}+B_{2,j}(\alpha _{2})_{i}+\cdots +B_{n,j}(\alpha _{n})_{i}$

Mas a $(\alpha _{j})_{i},$ a $i$-ésima entrada à linha $\alpha _{j},$ corresponde ao elemento $A_{i,j},$ de modo que também obtemos a fórmula acima.

Portanto,

Propriedades

A multiplicação de matrizes tem as seguintes propriedades:

• Associativa:

  $(AB)C=A(BC)$

• Distributiva em relação à Adição:

  $(A+B)C=AC+BC$

• Elemento Neutro: se $A$ é uma matriz $m\times n,$ então

  $I_{m}A=AI_{n}=A,$ onde $I_{n}$ representa a matriz identidade de ordem $n.$

Note que, em geral, a multiplicação de matrizes não é comutativa, ou seja, geralmente tem-se $AB\neq BA.$ Em muitos dos casos, a multiplicação $BA$ pode não estar sequer definida: quando existe a multiplicação $AB,$ a multiplicação $BA$ só pode existir no caso em que $A$ e $B$ são quadradas; mesmo assim, ainda pode ocorrer a não-comutatividade.

Transposição

Definição

A operação de transposição de uma matriz $A$ retorna como resultado sempre um matriz $B$ tal que, para todo elemento de $A$ e $B,$ $a_{ij}=b_{ji}.$ $B$ é então dita a matriz transposta de $A,$ denotada por $A^{t}.$

• O número de linhas da matriz transposta será igual ao número de colunas da matriz original, assim como o número de colunas da transposta será igual ao número de linhas da original. Ou seja, se $A$ era $m\times n,$ $A^{t}$ será $n\times m.$
• Cada coluna de $A$ corresponderá a uma linha de $A^{t},$ e vice-versa.

Ver também

• Matemática elementar/Matrizes (livro com conteúdo mais simples)

Determinantes

Em matemática, determinante é uma função matricial que associa a cada matriz quadrada um escalar; ela transforma essa matriz em um número real. Esta função permite saber se a matriz tem ou não inversa, pois as que não têm são precisamente aquelas cujo determinante é igual a 0.

Definição

Seja $\mathrm {M}$ o conjunto das matrizes com n linhas e n colunas sobre um corpo k. Pode-se provar que existe uma única função $f$ com as seguintes propriedades:

1. $f$ é n-linear e alternada nas linhas das matrizes;
2. $f$ ($\mathrm {I}$$n$) onde $I$$n$ é a matriz identidade.

Esta função denomina-se de determinante.

O determinante de uma matriz $A$ representa-se por $\mid A\mid$ ou por $det(A)$.

Matrizes 3x3

O determinante de matrizes de ordem 3 pode ser encontrado pela Regra de Sarrus, na qual a matriz é extendida repetindo as duas primeiras colunas, de modo que seja obtida uma sequência de 5 colunas. Em seguida, é somado os produtos das três diagonais principais (que partem de cima para baixo) e subtraído os produtos das três diagonais secundárias (que vão de baixo para cima). Seja a matriz de ordem 3 $M$, o determinante pode ser dado por:

${\textstyle \det(M)={\begin{vmatrix}a_{11}&a_{12}&a_{13}\\a_{21}&a_{22}&a_{23}\\a_{31}&a_{32}&a_{33}\end{vmatrix}}=a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32}-a_{31}a_{22}a_{13}-a_{32}a_{23}a_{11}-a_{33}a_{21}a_{12}.}$

Cofator de uma matriz

É um número associado a um elemento qualquer de uma matriz quadrada. Compreender o cofator é um pré-requisito para o estudo do Teorema de La Place, que é comumente usada para calcular determinantes de ordem maior que três. Cada elemento possui o seu respectivo cofator, que é representado pela seguinte expressão:

$Aij=(-1)^{i+j}det(Mij)$

O valor de $A$ é justamente o cofator do elemento $aij$. O ultimo termo diz respeito a determinante da matriz em questão sem os elementos da linha $i$ e da coluna $j$.

Calcule o determinante usando cofatores:

$A={\begin{bmatrix}1&0&-1&3\\2&3&4&2\\0&2&5&1\\4&1&0&0\end{bmatrix}}$

Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros.

Espaços vetoriais

A distribuição do conteúdo deste livro está confusa ou pouco didática (discuta). Pede-se aos editores que reavaliem a distribuição do mesmo.

Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros.

Definição

Um espaço vetorial é formado por:

1. Um conjunto qualquer $V,$ cujos elementos serão chamados de vetores;
2. Um corpo $K,$ cujos elementos serão denominados escalares, com elementos neutros distintos 0 e 1;
3. Uma operação $+:V+V\to V,$ conhecida como adição de vetores;
4. Uma operação $*:K\times V\to V,$ chamada de multiplicação por escalar.

Neste wikilivro, será escrito simplesmente $\alpha v$ para denotar $\alpha *v.$

Normalmente, o corpo K é o corpo dos números racionais, dos números reais ou dos números complexos.

Definição

Dizemos que $V$ é um espaço vetorial sobre $K$ quando as operações $+$ e $*$ satisfazem as seguintes propriedades:

Adição

1. Para cada $u,v\in V,$ $u+v\ =\ v+u$ (comutatividade)
2. Para cada $u,v,w\in V,$ $(u+v)+w\ =\ u+(v+w)$ (associatividade)
3. Existe um vetor $0,$ tal que para cada $u\in V,$ $0+u\ =\ u$ (neutro aditivo)
4. Para cada $u\in V,$ existe $-u\in V$ tal que $u+(-u)\ =\ 0$ (inverso aditivo)

Multiplicação por escalar

1. Para cada $\alpha \in K$ e cada $u,v\in V,$ $\alpha (u+v)\ =\ \alpha u+\alpha v$ (distributividade)
2. Para cada $\alpha ,\beta \in K$ e cada $u\in V,$ $(\alpha +\beta )u\ =\ \alpha u+\beta u$ (distributividade)
3. Para cada $\alpha ,\beta \in K$ e cada $u\in V,$ $(\alpha \beta )u\ =\ \alpha (\beta u)$ (associatividade)
4. Para cada $u\in V,$ $1u\ =\ u$ (neutro multiplicativo)

Exemplos

• $\mathbb {R} ^{2}\,$, $\mathbb {R} ^{3}\,$ e, mais geralmente, $\mathbb {R} ^{n}$, são espaços vetoriais reais (sobre o corpo $\mathbb {R}$), quando munidos da soma e multiplicação por escalar usuais.
• O conjunto formado pelo único número real 0, ou seja, {0}, é um espaço vetorial sobre $\mathbb {R} \,.$
• $\mathbb {R} \,$ é um espaço vetorial sobre $\mathbb {R} \,.$
• Os exemplos acima são aplicáveis para qualquer corpo K, ou seja, são espaços vetoriais sobre K: {0}, K e Kⁿ.
• Seja $n\in \mathbb {N}$ um número qualquer. O conjunto dos polinômios de grau menor ou igual a $n$ é um espaço vetorial, onde consideramos a soma de dois polinômios como a soma dos coeficientes de mesmo grau e a multiplicação por escalar como a multiplicação de cada coeficiente pelo escalar em questão.
• Seja $\mathbb {N} \,$ o conjunto dos números inteiros positivos, e S o conjunto de todas as funções de domínio $\mathbb {N} ^{*}\,$ e contradomínio $\mathbb {R} \,.$ Dadas f e g funções e λ um número real, podemos definir

(f + g) como a função que leva o número inteiro positivo n no número real f(n) + g(n)

(λ f) como a função que leva o número inteiro positivo n no número real λ f(n).

Ou seja, foram definidas as operações de soma de vetores e produto de um escalar por um vetor em S. Como exercício, podem-se provar os axiomas, mostrando que S é um espaço vetorial. Este espaço vetorial é tão importante que tem um nome: ele é o espaço vetorial das sequências de números reais.

• O exemplo acima pode ser generalizado. Seja K um corpo qualquer, e I um conjunto qualquer (a letra I é porque este conjunto será chamado de conjunto de índices). Então o conjunto K^I, das funções de domínio I e contra-domínio K, torna-se naturalmente um espaço vetorial definindo-se para $f,g\in K^{I}\,,$ $\lambda \in K\,:$

$(f+g)(x)=f(x)+g(x)\,$

$(\lambda f)(x)=\lambda f(x)\,$

O fato de um conjunto ser ou não um espaço vetorial depende fortemente das operações envolvidas. O próximo exemplo ilustra esta questão:

Exemplo: Verifique se $(\mathbb {R} ^{2},\oplus ,.)$, munido das operações

${\begin{cases}(x_{1},y_{1})\oplus (x_{2},y_{2})=(x_{1}+x_{2},y_{1}+y_{2})&\\k.(x_{1},y_{1})=(-kx_{1},-ky_{1})\end{cases}}$

é um espaço vetorial.

Com efeito, observe inicialmente que a a soma em questão é a usual. Logo, satisfaz as propriedades de espaço vetorial. Iremos provar que a a multiplicação por escalar não satisfaz o seguinte propriedade de espaço vetorial:

$1\cdot u=u$

De fato, se $u=(x_{1},y_{1})$, então $1.u=1(x_{1},y_{1})=(-1x_{1},-1y_{1})=(-x_{1},-y_{1})\neq (x_{1},y_{1})$. Portanto, $\mathbb {R} ^{2}$, munido destas operações, não é um espaço vetorial.

Subespaços vetoriais

Definição

Seja $V$ um espaço vetorial sobre o corpo $K.$ Um subespaço vetorial de $V$ é um subconjunto $W$ que também é um espaço vetorial sobre $K,$ com as mesmas operações (adição e multiplicação por escalar) de $V.$

Equivalentemente, um subespaço vetorial de $V$ é um subconjunto não-vazio $W$ fechado em relação às operações de adição e multiplicação por escalar, ou seja, um subconjunto tal que

1. Para todos $u,v\in W$ tem-se $u+v\in W;$
2. Para qualquer escalar $\lambda \in K$ e para todo $u\in W$ tem-se $\lambda u\in W.$

Exemplo: Seja $F=\{(x,2x,3x):x\in \mathbb {R} \}$. Provemos que $F$ é um subespaço vetorial.

1. O subconjunto $F$ é não-vazio, uma vez que o vetor nulo pertence a $F$. $$F\neq \emptyset ,{\text{ pois }}{\vec {0}}=(0,0,0)=(0,2.0,3.0)$$
2. O subconjunto $F$ é fechado em relação à soma. Considere os vetores $u$ e $v$ abaixo: $$u=(x_{1},2x_{1},3x_{1})\ \ \ \ \ \ v=(x_{2},2x_{2},3x_{2})$$A soma desses dois vetores resulta no vetor$$u+v=(x_{1}+x_{2},\ 2x_{1}+2x_{2},\ 3x_{1}+3x_{2})$$O vetor resultante da soma de $u$ e $v$ ainda se encontra presente em $F$, pois a segunda coordenada continua sendo o dobro da primeira e a terceira coordenada, o triplo da primeira.
3. O subconjunto $F$ é fechado em relação à multiplicação por escalar. Considere novamente o vetor $u$ abaixo: $$u=(x_{1},2x_{1},3x_{1})$$A multiplicação de $u$ por um escalar $\alpha \in \mathbb {R}$ resultará em: $$\alpha .u=(\alpha .x_{1},\alpha .2x_{1},\alpha .3x_{1})$$O vetor resultante dessa multiplicação ainda se encontra presente no subespaço $F$, pois a segunda coordenada continua sendo o dobro da primeira e a terceira coordenada, o triplo da primeira.

Combinação linear

Definições

Definição

Seja $V$ um espaço vetorial sobre um corpo $K.$ Um vetor $u\in V$ é dito combinação linear dos vetores $v_{1},\ldots ,v_{n}\in V$ se existem escalares $\lambda _{1},\ldots ,\lambda _{n}\in K$ tais que

$\lambda _{1}v_{1}+\cdots +\lambda _{n}v_{n}=u$

Note-se que, pela definição, nem os λ nem os v precisam ser distintos.

Definição

Seja S um subconjunto do espaço vetorial V. Um vetor $u\in V$ é dito uma combinação linear de elementos de S quando $u=0$ ou existem:

um número inteiro positivo n, $n\in \mathbb {N} ^{*}$

vetores $v_{1},\ldots ,v_{n}\in S$ e

escalares $\lambda _{1},\ldots ,\lambda _{n}\in K$

tais que

$\lambda _{1}v_{1}+\cdots +\lambda _{n}v_{n}=u$

Deve-se notar que a condição u = 0 é importante para o caso em que S seja o conjunto vazio. Equivalentemente, seria possível definir a soma de zero vetores como o vetor nulo (isto é semelhante à definição do fatorial de 0, igual ao produto de zero fatores, ou seja, é o elemento neutro multiplicativo, 1).

Propriedades

• Todo elemento x de S é uma combinação linear de elementos de S. Basta escolher n = 1, v₁ = x e λ = 1, de forma que x = λ v₁
• Se x é uma combinação linear de elementos de S, e λ é um escalar, então λ x também é uma combinação linear de elementos de S. Prova: x = 0 (neste caso, λ x = 0) ou $x=\lambda _{1}v_{1}+\ldots \lambda _{n}v_{n}\,.$ Então $\lambda x=(\lambda \lambda _{1})v_{1}+\ldots (\lambda \lambda _{n})v_{n})\,.$
• Se x e y são combinações lineares de elementos de S, então x + y também é. A prova é um pouco mais complicada, e será feita com cuidado
  • Caso x ou y sejam 0, é imediato que x + y, sendo igual a x ou y, é uma combinação linear de elementos de S.
  • No caso geral, $x=\lambda _{1}v_{1}+\ldots +\lambda _{n}v_{n}\,$ e $y=\mu _{1}w_{1}+\ldots +\mu _{m}w_{m}\,.$ Então definindo
    $\eta _{1}=\lambda _{1},\ldots \eta _{n}=\lambda _{n},\eta _{n+1}=\mu _{1},\ldots \eta _{n+m}=\mu _{m}\,$ e
    $u_{1}=v_{1},\ldots u_{n}=v_{n},u_{n+1}=w_{1},\ldots u_{n+m}=w_{m}\,,$ temos que
    $x+y=\eta _{1}u_{1}+\ldots +\eta _{n+m}u_{n+m}\,$
• Os últimos resultados mostram que o conjunto formado por todas as combinações lineares de elementos de S é um espaço vetorial - o capítulo seguinte estudará este espaço

Dependência e Independência linear

Definição

Seja $S$ um subconjunto de $V.$ Dizemos que $S$ é linearmente dependente se existem vetores distintos $v_{1},\ldots ,v_{n}\in V$ e escalares $\lambda _{1},\ldots ,\lambda _{n}\in K,$ não todos nulos, tais que

$\lambda _{1}v_{1}+\cdots +\lambda _{n}v_{n}=0$

Ou seja, $S$ é linearmente dependente se alguma combinação linear não-trivial de alguns de seus vetores resulta no vetor nulo. Quando $S$ não é linearmente dependente, ou seja, quando a única combinação linear de vetores de $S$ que resulta no vetor nulo é a trivial (com todos os coeficientes nulos), dizemos que $S$ é linearmente independente.

Quando temos um número finito de vetores $v_{1},\ldots ,v_{n},$ é comum dizer que os vetores $v_{1},\ldots ,v_{n}$ são linearmente dependentes (ou independentes), em vez de dizer que o conjunto $S=\{v_{1},\ldots ,v_{n}\}$ é linearmente dependente (ou independente).

Propriedades

• Pela definição, o conjunto vazio é linearmente independente.
• Todo conjunto que contém o vetor nulo é linearmente dependente.
• Todo conjunto que tem um subconjunto linearmente dependente é linearmente dependente.
• Todo subconjunto de um conjunto linearmente independente é linearmente independente.
• Se um vetor de um conjunto é combinação linear de outros vetores desse conjunto, então o conjunto é linearmente dependente.
• A interseção de dois conjuntos linearmente independentes é linearmente independente - podendo ser o conjunto vazio.
• A interseção de um número qualquer de conjuntos linearmente independentes é linearmente independente.
• A união de conjuntos linearmente independentes, normalmente, não será linearmente independente. Porém quando um conjunto é subconjunto de outro, a sua união (sendo igual ao maior conjunto) é linearmente independente. Uma extensão não-trivial desta propriedade é a seguinte: seja K um conjunto formado por conjuntos linearmente independentes, de modo que dados quaisquer dois elementos de K, um deles é subconjunto do outro. Então a união de todos os elementos de K também é linearmente independente.

Espaço gerado

Definição

Definição

Seja $S$ um subconjunto de um espaço vetorial $V.$ O conjunto de todas as combinações lineares finitas de elementos de $S$ é um subespaço $W$ de $V,$ e é dito o subespaço gerado por $S.$ Quando $S$ é um conjunto finito $\{v_{1},\ldots ,v_{n}\},$ dizemos que $W$ é o subespaço gerado pelos vetores $v_{1},\ldots ,v_{n}.$

Exemplos

Este módulo tem a seguinte tarefa pendente: Elaborar e incluir uma imagem para ilustrar este conceito.

• Em qualquer espaço vetorial V, o espaço vetorial gerado pelo conjunto vazio é o subespaço vetorial { 0 }. Analogamente, o espaço vetorial gerado pelo conjunto V é o próprio V
• Em $\mathbb {R} ^{2}\,,$ o espaço vetorial gerado por um vetor não-nulo é uma reta que passa pela origem
• Em $\mathbb {R} ^{3}\,,$ o espaço vetorial gerado por um vetor não-nulo também é uma reta que passa pela origem
• Em $\mathbb {R} ^{2}\,,$ o espaço vetorial gerado por dois vetores não-nulos, em que um deles não é múltiplo do outro, é todo o $\mathbb {R} ^{2}\,$
• Em $\mathbb {R} ^{3}\,,$ o espaço vetorial gerado por dois vetores não-nulos, em que um deles não é múltiplo do outro, é um plano que passa pela origem

Definição através de conjuntos

Seja S um conjunto de vetores de V. Pode-se perguntar qual é o menor subespaço vetorial de V que contém S. Para ser mais preciso, temos o seguinte:

• V é um subespaço vetorial de V que contém S
• A interseção de subespaços vetoriais de V que contém S também é um subespaço vetorial de V

Ou seja, seja K o conjunto (não vazio, porque $V\in K\,$) definido por:

• $K=\{W\subseteq V\ |\ (W{\mbox{ subespaco vetorial de }}V)\land S\subseteq W\}\,$

e seja ${\bar {S}}\,$ definido por:

• ${\bar {S}}=\bigcap _{X\in K}X\,$

Teorema

Nas condições definidas acima, ${\bar {S}}\,$ é o subespaço vetorial gerado por S.

Bases

Definição

Seja $S$ um subconjunto de um espaço vetorial $V.$ $S$ é uma base do espaço vetorial $V$ quando o subespaço de $V$ gerado por $S$ é o próprio $V$ e $S$ é um conjunto linearmente independente. Quando uma base $S$ é um conjunto finito $\{v_{1},\ldots ,v_{n}\}$ de $n$ elementos, dizemos que $V$ tem dimensão $n$.

Seja V um espaço vetorial e B uma base de V. Suponha que um vetor $v\in V\,$ seja escrito como combinação linear de vetores de B de duas formas diferentes: $v=\lambda _{1}u_{1}+\ldots +\lambda _{n}u_{n}=\mu _{1}w_{1}+\ldots +\mu _{m}w_{m}\,.$ O que pode ser dito a respeito dos λ e μ? O que pode ser dito a respeito dos u_i e w_j? A resposta é que, de certa maneira, eles são únicos.

Coordenadas

Definição

Seja B uma base de um espaço vetorial V. Se existe $b\in B\,,$ então para todo vetor $v\in V,$ se expressarmos v como uma combinação linear de elementos de B que inclua b, o coeficiente do termo b será constante. Em outras palavras, para toda base B do espaço vetorial V existe uma função que associa a cada par $(v,b)\in V\times B\,$ um escalar. Esta função é chamada de a coordenada de v na base B

Ver também

Wikipédia

• Espaço vetorial
• Subespaço vetorial
• Independência linear
• Espaço vetorial gerado
• Base

Transformações lineares

A distribuição do conteúdo deste livro está confusa ou pouco didática (discuta). Pede-se aos editores que reavaliem a distribuição do mesmo.

Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros.

Transformações Lineares

Definição

Definição

Uma função $T:V\to W,$ onde $V$ e $W$ são espaços vetoriais sobre um corpo $K,$ é dita uma transformação linear se, para todos $u,v\in V$ e para todo $\lambda \in K,$ tem-se

$\;T(u+v)=T(u)+T(v)$

$T(\lambda u)=\lambda \,T(u)$

Existência de uma transformação

Sejam V e W espaços vetoriais sobre um corpo K, onde a $dim\;V<\infty$. Seja $\{v_{1},v_{2},...,v_{n}\}\;$ uma base de V e $w_{1},w_{2},...,w_{n}\;$ vetores quaisquer de W. Então existe uma transformação linear $T:V\mapsto W,Tv_{i}=w_{i},i=1,...,n$.

Prova

T existe e está bem definida Dado $v\in V,\exists x=(x_{1},...,x_{n}),x_{i}\in K,i=1,...,n$ tal que $v=\sum _{i=1}^{n}x_{i}v_{i}$. Podemos definir T em v como $Tv=\sum _{i=1}^{n}x_{i}w_{i}$. Sendo $\{v_{1},v_{2},...,v_{n}\}\;$ uma base, tem-se a unicidade de $(x_{1},...,x_{n})$ e, consequentemente, T está bem definida por meio da regra que associa o vetor $v\in V$ ao vetor $Tv\in W$. Vemos através da definição que $Tv=\sum _{i=1}^{n}x_{i}Tv_{i}=\sum _{i=1}^{n}x_{i}w_{i}\Rightarrow Tv_{i}=w_{i},i=1,...,n$. T é linear Tome $w\in V,w=\sum _{i=1}^{n}y_{i}v_{i},c\in K$. Assim $cv+w=c\sum _{i=1}^{n}x_{i}v_{i}+\sum _{i=1}^{n}y_{i}v_{i}=\sum _{i=1}^{n}(cx_{i}+y_{i})v_{i}$. Pela definição $T(cv+w)=\sum _{i=1}^{n}(cx_{i}+y_{i})w_{i}$. De outro modo $cTv+Tw=c\sum _{i=1}^{n}x_{i}w_{i}+\sum _{i=1}^{n}y_{i}w_{i}=\sum _{i=1}^{n}(cx_{i}+y_{i})w_{i}$. Portanto $T(cv+w)=cTv+Tw\;$. T é única Suponha que exista $U:V\mapsto W,Uv_{i}=w_{i},i=1,...,n\;$, então se $v=\sum _{i=1}^{n}x_{i}v_{i}$, então $Uv=\sum _{i=1}^{n}x_{i}Uv_{i}=\sum _{i=1}^{n}x_{i}w_{i}=Tv,\forall v\in V$.

Imagem de uma transformação linear

A seguir será discutido um exemplo de como achar a imagem de uma transformação linear. Considere $T:\mathbb {R} ^{2}\rightarrow \mathbb {R} ^{2}$, definida por $T(x,y)=(2x+3y,4x-3y)$. O valor de $T$ em um ponto $(x,y)$ pode ser reescrito da seguinte forma:

$T(x,y)=(2x+3y,4x-3y)=x(2,4)+y(3,-3)$.

Consequentemente, todo ponto da imagem é uma combinação linear dos vetores $(2,4)$ e $(3,-3)$, isto é, tais vetores formam um conjunto de geradores para a imagem de $T$. Como poderá ser verificado pelo leitor, estes vetores também são linearmente independentes, constituindo portanto uma base para a imagem de $T$.

Núcleo

Definição

Seja $T:V\to W\,$ uma transformação linear entre os espaços vetoriais V e W. O núcleo da transformação linear, Ker(T), é a imagem inversa do vetor nulo em W:

$Ker(T)=\{v\in V|T(v)=0\}\,$

Teorema do núcleo

O núcleo de uma transformação linear é um subespaço vetorial do seu domínio

A demonstração é simples:

• Ker(T) não é vazio, pois 0_V é um elemento de Ker(T), já que T(0_V) = 0_W
• Se $v,w\in Ker(T)\,,$ então T(v) = T(w) = 0, logo, pela linearidade de T, T(v + w) = 0 e $v+w\in Ker(T)\,$
• Se $\lambda \in K\,$ e $v\in Ker(T)\,,$ temos $T(v)=0\,$ logo $T(\lambda v)=\lambda T(v)=\lambda 0=0\,,$ ou seja, $\lambda v\in Ker(T)\,$

Posto e nulidade

Se $dimV<\infty$, e $T:V\mapsto W$

• O posto(T) = dim Im(T),isto é, a dimensão da imagem de T(V), isto é, a quantidade de vetores L.I. que geram toda a imagem de T(V).

e

• A Nulidade(T) = dim Ker(T), isto é, é a dimensão do núcleo de T(V), isto é, a quantidade de vetores L.I. que geram todo o núcleo de T(V).

Teorema do posto e da nulidade

Sejam V e W espaço vetoriais sobre o corpo K e $T:V\mapsto W$. Se $dimV<\infty$, então posto(T) + Nulidade(T) = dim V

Prova

• Definindo a base do núcleo e a base do espaço:

Seja $\{v_{1},v_{2},...,v_{k}\}\;$ uma base do Ker(T). Existem vetores $v_{j},\;$ com j=k+1,...,n onde $\{v_{1},v_{2},...,v_{k},v_{k+1},...v_{n}\}\;$ é uma base de V.

• Definindo a base da imagem:

Como $\{v_{1},v_{2},...,v_{n}\}\;$ é a base de V, T aplicada nessa base gera um conjunto que gera a imagem de T por V. Aplicando T sobre os vetores da base de V, temos $Tv_{1},Tv_{2},...,Tv_{n}\;$, mas $Tv_{1}=Tv_{2}=...=Tv_{k}=0\;$, pela definição de núcleo. Assim os vetores $Tv_{k+1},...,Tv_{n}\;$ geram a imagem de T(V).

• Provando que os vetores são independentes:

Como queremos uma base, eles devem ser independentes, isto é, devem $\exists c_{i}\in K,$ tal que $\sum _{i=1}^{n}c_{i}v_{i}=0\Leftrightarrow c_{i}=0,i=1,...,n$.

Tomemos $\sum _{i=k+1}^{n}c_{i}(Tv_{i})=0\Leftrightarrow T(\sum _{i=k+1}^{n}c_{i}v_{i})=0$. Logo $w=\sum _{i=k+1}^{n}c_{i}v_{i}\in Ker(T)$. Como $w\in Ker(T),w=\sum _{i=1}^{k}b_{i}v_{i},b_{i}\in K$.

Portanto $w=\sum _{i=k+1}^{n}c_{i}v_{i}=\sum _{i=1}^{k}b_{i}v_{i}\Leftrightarrow \sum _{i=k+1}^{n}c_{i}v_{i}-\sum _{i=1}^{k}b_{i}v_{i}=0$. Como $v_{1},v_{2},...,v_{k}\;$ são L.I., então $b_{i}=c_{i}=0,\forall i=1,...,n$.

• Definindo posto e nulidade:

O Posto(T) = dim Im(T). Como $Tv_{k+1},...,Tv_{n}\;$ geram a imagem de T(V), logo o posto(T)= n - (k+1) +1 = n-k.

A nulidade (T) = dim Ker(T). Como $\{v_{1},v_{2},...,v_{k}\}\;$ é uma base do Ker(T), logo a Nulidade (T)= k - 1 + 1 = k

Como n = dim V, Nulidade(T)=k e Posto(T)=n-k, portanto Posto(T) + Nulidade(T) = dim(V).

Funcionais lineares

Definição

Definição

Uma função $f:V\rightarrow K,$ onde V é um espaço vetorial sobre K, é chamada de funcional linear se, $\forall u,v\in V$ e $\forall \lambda \in K:$

$f(u+v)=f(u)+f(v)$

$f(\lambda v)=\lambda f(v)$

Teorema  (existência e unicidade)

Se V é um espaço vetorial de dimensão n e $\alpha =\{v_{1},v_{2},\ldots ,v_{n}\}$ é uma base de V, então existe um único funcional f, tal que $f(v_{i})=\lambda _{i},i=1,2,\ldots ,n$ e $\lambda _{i}\in K$

Teorema  (base dual)

Se V é um espaço vetorial, $\mathrm {dim} V=n$ e $\beta =\{v_{1},v_{2},\ldots ,v_{n}\}$ é uma base de V, então existe uma única base $\beta ^{*}=\{f_{1},f_{2},\ldots ,f_{n}\}$ de $V^{*}$ tal que $f_{i}(v_{j})=\delta _{ij}$

Definição

$\beta ^{*}$ é chamada de base dual de $\beta$

$V^{*}$ é chamado de espaço dual de V

Corolários:

$f=\sum f(v_{i})f_{i}$

$v=\sum f_{i}(v)v_{i}$

Teoremas

Teorema  (representação dos funcionais lineares)

Sejam V um espaço vetorial sobre K, $\mathrm {dim} V=n,$ com produto interno, e $f:V\rightarrow K$ um funcional linear. Então existe um único vetor $v_{o}\in V,$ tal que $f(v)=\langle v,v_{o}\rangle ,$ $\forall v\in V.$

Demonstra-se ainda que $v_{o}=\sum {\overline {f(e_{i})}}e_{i}$

Operador linear

Dizemos que T uma transformação linear, $T:V\mapsto V$ é chamada operador linear de T sobre V.

Adjunto de um operador linear

Definição

Definição

Seja V um espaço vetorial. O operador adjunto, $T^{*}:V\rightarrow V,$ de um determinado operador linear $T:V\rightarrow V$ é definido pela igualdade:

$\langle T(u),v\rangle =\langle u,T^{*}(v)\rangle ,\quad \forall u,v\in V$

Demonstra-se que todo operador linear possui um e apenas um operador adjunto correspondente.

A partir da definição, podemos obter as seguintes conseqüências (prove!):

$(S+T)^{*}=S^{*}+T^{*}$

$(\lambda T)^{*}={\bar {\lambda }}T^{*}$

$(S\circ T)^{*}=T^{*}\circ S^{*}$

Proposição

Seja V um espaço vetorial sobre K, $\mathrm {dim} V=n,$ com produto interno. Seja $\alpha =\{e_{1},e_{2},\ldots ,e_{n}\}$ uma base ortonormal de V. Então $[T]_{\alpha }=(a_{ij}),$ onde $a_{ij}=\langle T(e_{j}),e_{i}\rangle$

Corolário

Seja V um espaço vetorial sobre K, $\mathrm {dim} V=n,$ com produto interno. Então, para qualquer base $\alpha =\{e_{1},e_{2},\ldots ,e_{n}\}$ ortonormal de V, temos que a matriz $[T^{*}]_{\alpha }=({\overline {[T]_{\alpha }}})^{t}.$

Operadores especiais

• Auto-adjunto ($T^{*}=T$)
• Unitário ($T^{*}=T^{-1}$)
• Normal ($T^{*}T=TT^{*}$)

Operador auto-adjunto

Definição

$T:V\rightarrow V$ é chamado de auto-adjunto se $T^{*}=T.$

Uma matriz A é auto-adjunta se ${\overline {A}}^{t}=A.$

• Se $K=R,$ $[T]_{\alpha }$ é chamada simétrica.
• Se $K=C,$ $[T]_{\alpha }$ é chamada hermitiana.

Os seguintes enunciados são úteis na prova de teoremas do operador auto-adjunto:

Se $\langle T(u),v\rangle =0,\forall u,v\in V,$ então $T=0.$

Se V é complexo e $\langle T(u),u\rangle =0,\forall u\in V,$ então $T=0.$

Prove:

• Se $T^{*}=T$ e $\langle T(u),u\rangle =0,\forall u\in V,$ então $T=0.$
• Seja $T:V\rightarrow V,$ com V complexo. Então $T^{*}=T\iff \langle T(v),v\rangle \in R.$

Operador unitário

Definição

$T:V\rightarrow V$ é chamado de unitário se $T^{*}=T^{-1}.$

Uma matriz A é unitária se ${\overline {A}}^{t}=A^{-1}$

Prove:

• T é unitário $\iff \langle T(u),T(v)\rangle =\langle u,v\rangle$ (T preserva o produto interno)
• T é unitário $\iff |T(u)|=|u|$ (T preserva a norma)
• T é unitário $\iff T^{-1}$ é unitário

Operador normal

Definição

$T:V\rightarrow V$ é chamado de normal se $TT^{*}=T^{*}T.$

Uma matriz A é normal se $AA^{*}=A^{*}A$

Prove:

• Todo operador auto-adjunto é normal
• Todo operador unitário é normal

É importante ressaltar, ainda, que existem operadores normais que não são unitários nem auto-adjuntos.

Subespaço invariante

Definição

Definição

W, subespaço vetorial de V, é dito invariante sob o operador $T:V\rightarrow V,$ se $T(W)\subset W.$

Dizemos também que W é T-invariante.

Exercícios

Prove:

• Se W é T-invariante, então $W^{\perp }$ é $T^{*}$-invariante.
• Se W é T-invariante e T é auto-adjunto, então W é $T^{*}$-invariante.
• Se W é T-invariante e T é inversível, então $T(W)=W.$
• Se W é T-invariante e T é inversível, então W é $T^{-1}$-invariante e $T^{-1}(W)=W.$
• Se W é T-invariante e T é unitário, então W é $T^{-1}$-invariante (ou $T^{*}$-invariante).
• Se W é T-invariante e T é unitário, então $W^{\perp }$ é T-invariante.

Ver também

Wikipédia

• Núcleo da transformação linear
• Transformação linear

Polinômios

Álgebra linear

Seja A, uma álgebra linear sobre o corpo K, então A é um espaço vetorial com uma operação extra, que é multiplicação de vetores, que onde dois vetores u, v de A são levados ao vetor uv de A, que é o produto dos vetores u e v. As propriedades desse produto são:

• multiplicação é associativa: u(vw) = (uv)w.
• multiplicação é distributiva em relação à adição: u(v + w) = uv + uw(à esquerda) e (u + v)w = uw + vw(à direita).
• multiplicação por escalar: k(uv) = (ku)v = u(kv).

Extensões de uma álgebra linear

• com elemento unidade: se existir um elemento i em A, tal que iu = ui = u, para todo u em A
• comutativa: se uv = vu para todo u,v em A

Álgebra dos polinômios

Seja P[x] o espaço dos polinômios finitos, gerados pelos vetores $1,x,x^{2},...,x^{n}\;$, pata algum n inteiro qualquer. P[x] é um polinômio sobre o corpo K.

• Definição da elemento de P[x].
  • $p(x)=c_{0}x^{0}+c_{1}x^{1}+...+c_{n}x^{n}+0x^{n+1}+0x^{n+2}+...=c_{0}+c_{1}x+...+c_{n}x^{n},\;$ onde $c_{k}=0,\forall k>n\;$.

• grau de p(x) em P[x]:
  • $gr(p)=n\;$, usando o p definido acima.

• coeficientes de p(x):
  • $c_{0},c_{1},...,c_{n}\;$ são chamados os coeficientes do polinômio p(x).

• polinômio nulo:
  • $p(x)=0\;$.

• polinômio não-nulo:
  • $p(x)\not =0\;$.

• polinômio unitário:
  • Se $gr(p)=n,c_{n}=1\;$, então p(x) é unitário.

Teoremas

Propriedade do Grau do produto de polinômios

Sejam p, q em P[x]-{0} sobre K. Então:

• pq é um polinômio não-nulo.
• gr(pq)=gr(p)+gr(q).
• se p,q são unitários, então pq é unitário.
• pq é polinômio constante $\Leftrightarrow \;$ pq são polinômios constantes.

Ideais de polinômios

Lema

Sejam p,q em P[x]-{0} sobre K, onde $gr(q)\leq gr(p)$. Logo existe r em P[x] tal que p-qr=0 ou gr(p-qr)<gr(p).

Formas canônicas elementares

Autovetores e autovalores

Definição

Seja V um espaço vetorial sobre K, e seja T um operador linear sobre V. Um vetor não nulo $v$ de V é dito um autovetor (ou vector próprio) de T se existir um $\lambda \in K$ tal que $T(v)=\lambda v\;$. Neste caso, $\lambda \;$ é dito autovalor (ou valor próprio) de T.

Um significado prático:

• Os autovetores são vetores que, sob a ação de um operador linear, resultam num vetor de mesma direção. Os autovetores estão sempre ligados ao operador linear, ou seja, cada operador linear admite um conjunto específico de autovetores.
• Para cada autovalor $\lambda \;$, podem existir vários autovetores $v\;$ tais que $T(v)=\lambda v\;$. Dizemos que esses são autovetores associados ao autovalor $\lambda \;$. Haverá infinitos autovetores associados a cada autovalor, exceto no caso do corpo K ser um corpo finito.

Prove:

• Se v é um autovetor de T associado ao autovalor $\lambda$, e $a\in K\,$ é um escalar não-nulo, então $av$ também é um autovetor associado a $\lambda$.
• O conjunto $V_{\lambda }=\{v\in V|T(v)=\lambda v\}$ é um subespaço vetorial de V (ele é chamado de autoespaço). Note que $V_{\lambda }$ é o conjunto de todos os autovetores associados a $\lambda$ unido ao vetor nulo.

$T-\lambda I$: um operador importante

O operador $(T-\lambda I):V\mapsto V$, leva os autovetores no vetor nulo

Como $(T-\lambda I)(v)=0,\forall v\in V_{\lambda }$. Logo $V_{\lambda }\;$ é o núcleo da transformação de $T-\lambda I$.

Teorema do operador $T-\lambda I$

Seja $T-\lambda I$ um operador linear sobre V de dimensão finita e $\lambda$ um valor característico do operador T sobre V. O operador $T-\lambda I$ é singular, se e somente se, det($T-\lambda I$)=0.

Prova:

• Definindo uma matriz associada ao operador

O operador $T-\lambda I$ é singular, ou seja, não é injetor. Existe uma matriz $A=[T]_{\beta },\beta \;$ é a base do operador T sobre V. Assim tome $\forall v\in V,(T-\lambda I)(v)=T(v)-\lambda I(v)=Av-\lambda I(v)=(A-\lambda I)(v)$, ou seja, $\forall v\in V,(T-\lambda I)(v)=(A-\lambda I)(v)$.

• calculando a determinante sobre o polinômio

Autovetores de uma matriz quadrada

Definição

Um autovalor de uma matriz $A_{n\times n}$ é um escalar $\lambda \in K$ tal que existe um vetor não nulo v, com $Av=\lambda v\;$, onde v é chamado de autovetor de A associado a $\lambda \;$.

$v={\begin{pmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{pmatrix}}$

Polinômio característico

Definição

Seja A uma matriz quadrada de ordem n. O polinômio $p(\lambda )=\det(A-\lambda I)$ é chamado de polinômio característico de A.

Prove:

• Seja $\alpha =\{v_{1},\ldots ,v_{n}\}$ uma base de V, e v um autovetor de T associado ao autovalor $\lambda \;$. Então $[v]_{\alpha }\;$ é um autovetor da matriz $[T]_{\alpha }\;$ associado ao autovalor $\lambda \;$ de $[T]_{\alpha }\;$
• Se $\alpha \;$ e $\beta \;$ são duas bases quaisquer de V, então o polinômio característico de $[T]_{\alpha }\;$ é igual ao polinômio característico de $[T]_{\beta }\;$.

Exemplo:

Operador diagonalizável

Definição

Um operador T é dito diagonalizável se existir uma base $\alpha =\{v_{1},\ldots ,v_{n}\}$ de V tal que $[T]_{\alpha }$ é uma matriz diagonal.

Definição

Duas matrizes quadradas de mesma ordem, A e B, são ditas semelhantes se existir uma matriz P, de mesma ordem, inversível, tal que $B=P^{-1}AP$.

Definição

Uma matriz $A_{n}$ é dita diagonalizável se $A_{n}$ for semelhante a uma matriz diagonal D (ou seja, existe uma matriz P, inversível, tal que $D=P^{-1}AP$).

Prove:

• Se $\alpha =\{v_{1},\ldots ,v_{n}\}$ são autovetores de T associados, respectivamente, aos autovetores $\alpha _{1},\ldots ,\alpha _{n}$ tais que $\lambda _{i}\neq \lambda _{j}$ se $i\neq j$, então $\alpha$ é LI.
• Seja $\alpha =\{v_{1},\ldots ,v_{n}\}$ uma base de V. A matriz $[T]_{\alpha }$ é diagonal $\iff \alpha$ é uma base de V formada por autovetores de T
• Se T é auto-adjunto e $\lambda$ é um autovalor de T, então $\lambda \in R$.
• Se T é auto-adjunto e $v_{1},\ldots ,v_{n}$ são autovetores de T associados aos autovalores $\alpha _{1},\ldots ,\alpha _{n}$ (distintos), respectivamente, então $v_{i}\perp v_{j}$, se $i\neq j$.
• Se T é unitário e $\lambda$ é um autovalor de T, então $|\lambda |=1$.
• Se $\lambda$ é um autovalor de T e T é normal, então ${\overline {\lambda }}$ é autovalor de $T^{*}$.
• $V_{\lambda }$ é T-invariante.
• $V_{\lambda }^{\perp }$ é $T^{*}$-invariante.
• Se T é normal e $\lambda$ é autovalor de T, então $V^{\perp }$ é $T^{*}$-invariante.
• Se T é normal, então $V_{\lambda }^{\perp }$ é T-invariante.

Produto interno

Em Álgebra linear, chamamos de produto interno uma função de dois vetores que satisfaz determinados axiomas. O produto escalar, comumente usado na geometria euclidiana, é um caso especial de produto interno.

Definição

Seja V um espaço vetorial sobre um corpo K. Em V, pode-se definir a função binária $\langle \cdot ,\cdot \rangle :V\times V\rightarrow K$ (denominada produto interno), que satisfaz os seguintes axiomas:

$\langle u,v\rangle ={\overline {\langle v,u\rangle }}$

$\langle u+v,w\rangle =\langle u,w\rangle +\langle v,w\rangle$

$\langle \lambda u,v\rangle =\lambda \langle u,v\rangle$

Se $v\neq 0$, então $\langle v,v\rangle$> $0$

em que u, v e w são vetores de V, e λ é um elemento de K.

A partir desses axiomas, é possível provar as seguintes consequências:

$\langle u,v+w\rangle =\langle u,v\rangle +\langle u,w\rangle$

$\langle u,\lambda v\rangle ={\overline {\lambda }}\langle u,v\rangle$

Se $v=0$, então $\langle v,v\rangle =0$

Se $\langle v,v\rangle =0$, então $v=0$

Exemplos

O produto escalar sobre o espaço vetorial $\mathbb {R} ^{3}$ satisfaz os axiomas do produto interno e é definido por:

$\langle (x_{1},y_{1},z_{1}),(x_{2},y_{2},z_{2})\rangle =x_{1}x_{2}+y_{1}y_{2}+z_{1}z_{2}$

Se f e g são duas funções contínuas em um intervalo fechado, é possível definir o produto interno:

$\langle f,g\rangle =\int f(x){\overline {g(x)}}\,dx$

Vetores ortogonais

Diz-se que dois vetores $u,v\in V$ são ortogonais se $\langle u,v\rangle =0$.

Consequências (prove!):

Se $\langle u,v\rangle =0,\forall v\in V$, então $u=0$

Se $\langle T(u),v\rangle =0,\forall u,v\in V$, então $T=0$

Complemento ortogonal

Seja $v\in V,v\neq 0$

Define-se o complemento ortogonal de v, $v^{\perp }$, como:

$v^{\perp }=\{v\}^{\perp }=\{u\in V|\langle u,v\rangle =0\}.$

Consequências (prove!):

$v^{\perp }$ é um subespaço vetorial de V

Seja $W$ um subespaço vetorial de V, e $\alpha =\{v_{1},v_{2},\ldots ,v_{n}\}$ uma base de $W$. $v\in W^{\perp }\iff v\in v_{i}^{\perp },i=1,\ldots ,n$

$(W^{\perp })^{\perp }=W$, W é subespaço de V.

Norma

Seja V um espaço vetorial sobre o corpo K, com produto interno. Define-se a norma ou comprimento de um vetor $v\in V$ como sendo o número ${\sqrt {\langle v,v\rangle }}$, que indicamos por $|v|$.

Consequências (prove!):

$|v|=0\Longleftrightarrow v=0$

Se $v\neq 0$, então $|v|>0$

$|\lambda v|=|\lambda ||v|,\forall \lambda \in K,v\in V$

Se $\langle u,v\rangle =0$, então $|u+v|^{2}=|u|^{2}+|v|^{2}$ (Teorema de Pitágoras)

Projeção ortogonal

Projeção de um vetor v na direção de um vetor u, em que u ≠ 0

Define-se essa projeção como sendo o vetor

${\mbox{proj}}_{u}v={\frac {\langle v,u\rangle }{\langle u,u\rangle }}\cdot u$

Projeção de um vetor v sobre um subespaço vetorial W de V

Seja $W=[u_{1},u_{2}]$, em que $\{u_{1},u_{2}\}$ é uma base ortogonal de W.

${\mbox{proj}}_{W}v={\mbox{proj}}_{u_{1}}v+{\mbox{proj}}_{u_{2}}v$

Desigualdade de Cauchy-Schwarz

Dados $u,v\in V$, então $|\langle u,v\rangle |\leq |u|\cdot |v|$

Desigualdade triangular

$|u+v|\leq |u|+|v|,\forall u,v\in V$

Base ortogonal e ortonormal

Uma base $\{v_{1},v_{2},\ldots ,v_{n}\}$ de V é dita ortonormal se $\langle v_{i},v_{j}\rangle =\delta ij$, em que

$\delta ij=1$, se i = j

$\delta ij=0$, se i ≠ j

A base é ortogonal se os vetores são ortogonais dois a dois.

v1.v2=0

Propriedade: n vetores não-nulos e ortogonais dois a dois, em um espaço de dimensão n, são linearmente independentes.

Processo de ortogonalização de Gram-Schmidt

Dada uma base $\{v_{1},v_{2},\ldots ,v_{n}\}$ de V, podemos encontrar, a partir desta base, uma base ortogonal $\{u_{1},u_{2},\ldots ,u_{n}\}$ de V.

$u_{i}=v_{i}-\sum _{k=1}^{i-1}{\frac {\langle v_{i},u_{k}\rangle }{\langle u_{k},u_{k}\rangle }}u_{k}$

Distância entre dois vetores

Define-se a distância entre dois vetores quaisquer, u e v, como sendo $d(u,v)=|u-v|$

Uma função distância tem as seguintes propriedades:

$d(u,v)\geq 0$

$\quad d(u,v)=0\Leftrightarrow u=v$

$d(u,v)=d(v,u)$

$d(u,v)\leq d(u,w)+d(w,v)$

Tais propriedades podem ser facilmente verificadas pela definição de norma.

Melhor aproximação de um vetor v de V por um vetor de W, subespaço vetorial de V

Se $d(v,u)\leq d(v,u'),\forall u'\in W$, então u é o vetor de W que dá a aproximação mais adequada de v por um vetor de W.

Demonstra-se que $u=proj_{W}v$

Formas bilineares e quadráticas

Formas bilineares

Definição

Uma função g do produto cartesiano $V\times V\rightarrow K$ (onde V é um espaço vetorial de dimensão finita sobre o corpo K) é dita bilinear se, $\forall u,v,w\in V,\lambda \in K$:

• $g(u+v,w)=g(u,w)+g(v,w)$
• $g(\lambda u,v)=\lambda g(u,v)$
• $g(u,v+w)=g(u,v)+g(u,w)$
• $g(u,\lambda v)=\lambda g(u,v)$

Matriz associada a uma forma bilinear

Sejam $g:V\times V\rightarrow K$ uma forma bilinear, e $\alpha =\{v_{1},v_{2},\ldots ,v_{n}\}$ uma base de V. Sejam X e Y dois vetores de V, sob a forma de matriz coluna:

$X={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}},Y={\begin{pmatrix}y_{1}\\y_{2}\\\vdots \\y_{n}\end{pmatrix}}$

Então:

$g(X,Y)=X^{t}AY\,$,

onde A é a matriz associada à forma bilinear g.

A matriz A é dada por:

${\begin{bmatrix}a_{11}&\cdots &a_{1n}\\\vdots &\ddots &\vdots \\a_{n1}&\cdots &a_{nn}\end{bmatrix}}$

onde $a_{ij}=f(v_{i},v_{j})\,$

Formas bilineares simétricas

Definição

Uma forma bilinear $g:V\times V\rightarrow K$ é dita simétrica se $g(u,v)=g(v,u)$

Proposição: $g:V\times V\rightarrow K$ é uma forma bilinear simétrica se, e somente se, a matriz associada à forma bilinear é simétrica em qualquer base de V.

Formas quadráticas

Definição

Dada uma forma bilinear simétrica $g:V\times V\rightarrow K$, dizemos que a função $f:V\rightarrow K$, definida por $f(v)=g(v,v)$, é a forma quadrática associada à forma bilinear g.

Note que:

• $f(u+v)=f(u)+2g(u,v)+f(v)$
• $f(\lambda v)=\lambda ^{2}f(v)$

Fórmulas de polarização

As fórmulas de polarização permitem que, dada a forma quadrática f, se descubra a forma bilinear g que a originou. Eis duas dessas fórmulas:

• $g(u,v)={\frac {1}{4}}\left(f(u+v)-f(u-v)\right)$
• $g(u,v)={\frac {1}{2}}\left(f(u+v)-f(u)-f(v)\right)$

Autovetores

Autovetores e autovalores

Definição

Seja V um espaço vetorial sobre K, e seja T um operador linear sobre V. Um vetor não nulo $v$ de V é dito um autovetor (ou vector próprio) de T se existir um $\lambda \in K$ tal que $T(v)=\lambda v$. Neste caso, $\lambda$ é dito autovalor (ou valor próprio) de T.

Um significado prático:

• Os autovetores são vetores que, sob a ação de um operador linear, resultam num vetor de mesma direção. Os autovetores estão sempre ligados ao operador linear, ou seja, cada operador linear admite um conjunto específico de autovetores.
• Para cada autovalor $\lambda$, podem existir vários autovetores $v$ tais que $T(v)=\lambda v$. Dizemos que esses são autovetores associados ao autovalor $\lambda$. Haverá infinitos autovetores associados a cada autovalor, exceto no caso do corpo K ser um corpo finito.

Prove:

• Se v é um autovetor de T associado ao autovalor $\lambda$, e $a\in K\,$ é um escalar não-nulo, então $av$ também é um autovetor associado a $\lambda$.
• O conjunto $V_{\lambda }=\{v\in V|T(v)=\lambda v\}$ é um subespaço vetorial de V (ele é chamado de autoespaço). Note que $V_{\lambda }$ é o conjunto de todos os autovetores associados a $\lambda$ unido ao vetor nulo.

Autovetores de uma matriz quadrada

Definição

Um autovalor de uma matriz $A_{n\times n}$ é um escalar $\lambda \in K$ tal que existe um vetor X, com $AX=\lambda X$, onde X é chamado de autovetor de A associado a $\lambda$.

$X={\begin{pmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{pmatrix}}$

Polinômio característico

Definição

Seja A uma matriz quadrada de ordem n. O polinômio $p(\lambda )=\det(A-\lambda I)$ é chamado de polinômio característico de A.

Prove:

• Seja $\alpha =\{v_{1},\ldots ,v_{n}\}$ uma base de V, e v um autovetor de T associado ao autovalor $\lambda$. Então $[v]_{\alpha }$ é um autovetor da matriz $[T]_{\alpha }$ associado ao autovalor $\lambda$ de $[T]_{\alpha }$
• Se $\alpha$ e $\beta$ são duas bases quaisquer de V, então o polinômio característico de $[T]_{\alpha }$ é igual ao polinômio característico de $[T]_{\beta }$.

Operador diagonalizável

Definição

Um operador T é dito diagonalizável se existir uma base $\alpha =\{v_{1},\ldots ,v_{n}\}$ de V tal que $[T]_{\alpha }$ é uma matriz diagonal.

Definição

Duas matrizes quadradas de mesma ordem, A e B, são ditas semelhantes se existir uma matriz P, de mesma ordem, inversível, tal que $B=P^{-1}AP$.

Definição

Uma matriz $A_{n}$ é dita diagonalizável se $A_{n}$ for semelhante a uma matriz diagonal D (ou seja, existe uma matriz P, inversível, tal que $D=P^{-1}AP$).

Prove:

• Se $\alpha =\{v_{1},\ldots ,v_{n}\}$ são autovetores de T associados, respectivamente, aos autovetores $\alpha _{1},\ldots ,\alpha _{n}$ tais que $\lambda _{i}\neq \lambda _{j}$ se $i\neq j$, então $\alpha$ é LI.
• Seja $\alpha =\{v_{1},\ldots ,v_{n}\}$ uma base de V. A matriz $[T]_{\alpha }$ é diagonal $\iff \alpha$ é uma base de V formada por autovetores de T
• Se T é auto-adjunto e $\lambda$ é um autovalor de T, então $\lambda \in R$.
• Se T é auto-adjunto e $v_{1},\ldots ,v_{n}$ são autovetores de T associados aos autovalores $\alpha _{1},\ldots ,\alpha _{n}$ (distintos), respectivamente, então $v_{i}\perp v_{j}$, se $i\neq j$.
• Se T é unitário e $\lambda$ é um autovalor de T, então $|\lambda |=1$.
• Se $\lambda$ é um autovalor de T e T é normal, então ${\overline {\lambda }}$ é autovalor de $T^{*}$.
• $V_{\lambda }$ é T-invariante.
• $V_{\lambda }^{\perp }$ é $T^{*}$-invariante.
• Se T é normal e $\lambda$ é autovalor de T, então $V^{\perp }$ é $T^{*}$-invariante.
• Se T é normal, então $V_{\lambda }^{\perp }$ é T-invariante.

Teoremas espectrais

Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros.

Os teoremas espectrais são muito importantes na álgebra Linear, pois garantem a existência de uma base ortonormal de autovetores para alguns tipos de operadores. Como visto, isto implica que o operador é diagonalizável, o que facilita bastante os cálculos.

Teorema espectral para operadores auto-adjuntos

Seja $T:V\rightarrow V$ um operador auto-adjunto e V um espaço vetorial complexo ou real de dimensão n. Então existe uma base ortonormal de V formada por autovetores de T.

Teorema espectral para operadores unitários

Seja $T:V\rightarrow V$ um operador unitário e V um espaço vetorial complexo de dimensão n. Então existe uma base ortonormal de V formada por autovetores de T.

Estilo

Nesta página estarão indicadas as convenções adotadas neste wikilivro, no que diz respeito a sua formatação. Recomenda-se a leitura do mesmo, por todos que pretendem contribuir com a melhoria desde texto.

Dicas

Observações

• Sempre que for dar uma dica ao leitor, utiliza a faixa acima. Isso oferece um destaque à sugestão que estiver sendo dada.
• Esta faixa é criada usando a predefinição {{CaixaMsg}}.

Definições

Definição

Uma definição pode ser entendida como o texto que explica de forma precisa o significado de um conceito.

Observações

• Geralmente um termo importante aparece pela primeira vez em uma definição.
• Devido à sua importância, é bom destacar a definição do restante do texto.
• No momento, a forma de destacar uma definição neste wikilivro é a inclusão da mesma dentro de uma região com bordas duplas, como no exemplo acima. Para isso, utiliza-se a predefinição {{Definição}}.
• O conceito que está sendo definido tem sido colocado em negrito, sendo que o texto da explicação tem sido alinhado a esquerda.

Exemplos

Observações

• Novamente, utiliza-se a predefinição {{CaixaMsg}} para posicionar uma faixa azul e uma imagem no lado esquerdo do exemplo.
• Note que não há bordas em torno dos exemplos.

Propriedades

Teorema

Sempre que uma propriedade importante dos objetos tratados no texto precisa ser destacada, isto deve ser feito em uma caixa como essa.

Observações

• Os principais tipos de propriedades a ser destacados são: teoremas, corolários e pequenos lemas.
• Para conseguir a formatação acima, utiliza-se a predefinição {{Teorema}}.

Índice remissivo

Nesta página estão listados os conceitos abordados neste livro em ordem alfabética.

O nome de cada conceito possui um link para a página onde o mesmo é definido. Outras ocorrências importantes do conceito são indicadas pelos links numerados, logo após o link principal.

A

• Associatividade

• Adição

de matrizes

de vetores

• Adjunta

de uma matriz

de uma transformação linear

• Auto-subespaço
• Autovalores

cálculo

complexos

de matrizes reais

definição

de matrizes auto-adjuntas

de matrizes simétricas positivas

e determinantes

generalizados

produto

sensibilidade

soma

• Autovetor

B

• Base

de um espaço vetorial

canônica

complexa

dual

ordenada

ortogonal

ortonormal

• Bidiagonalização
• Bi-dual

C

• Caminho em um grafo
• Circuitos elétricos
• Codificação de mensagens
• Coeficiêntes de Fourier
• Cofatores
• Combinação

convexa

linear

• Complemento ortogonal
• Completamento de quadrados
• Complexificação de um espaço vetorial
• Comprimento

de um caminho (em um grafo)

de um vetor

• Comutatividade
• Condições de Penrose
• Cone
• Cônica
• Conjunto

convexo linearmente

dependente

independente

gerador

ortogonal

ortonormal

solução de um sistema linear

• Contagem das operações
• Coordenadas de um vetor
• Cosseno do ângulo entre dois vetores
• Criptografia

D

• Distributividade
• Decomposição

em valores singulares

definição

e mínimos quadráticos

e posto

e subespaços fundamentais

de Cholesky

de Schur

LDU

LU

polar

QR

• Deflação
• Descomplexificada
• Desenvolvimento de um determinante
• Desigualdade

de Cauchy-Schwarz

de Schwarz

triangular

• Deslocamentos da origem (no método das potências)
• Determinante

da transposta

de ordem 2

de um operador

de um produto

de uma matriz

singular

triangular

do operador descomplexificado

definição

e autovalores

e independência linear

expansão em cofatores

menor

propriedades

• Diagonalização
• Dimensão

de um espaço vetorial

de uma variedade afim

do núcleo

dos espaços linha e coluna

finita

infinita

• Distância

entre vetores

em um espaço vetorial normado

no espaço bidimensional

no espaço de dimensão $n$

• Distribuição

de autovalores

de números condicionais

E

• Equação linear
• Escalar, 1
• Espaço vetorial

I

• Inverso aditivo

M

• Multiplicação

de um escalar por uma matriz

de matrizes

• Matriz(es)

coluna

definição

diagonal

escalar

identidade

linha

nula

quadrada

triangular superior

triangular inferior

N

• Neutro aditivo
• Neutro multiplicativo

S

• Sistema de equações lineares
• Subespaços

vetoriais

triviais

T

• Transposição de matrizes

V

• Vetor

nulo

Z

Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros.

Faltam capítulos neste índice. Ampliando-o você ajudará a melhorar o Wikilivros.

Bibliografia

Livros

• Artin, Michael. Algebra. Englewood Cliffs: Prentice Hall, 1991. 672 p. ISBN 0130047635
• Halmos, Paul Richard. Finite-Dimensional Vector Spaces. Berlin: Springer, 1974. ISBN 0387900934
• Hoffman, Kenneth, Kunze, Ray. Linear Algebra. Englewood Cliffs: Prentice-Hall, 1971. 407 p. ISBN 0135367972
• Hogben, Leslie. Handbook of Linear Algebra. Boca Raton: CRC Press, 2007. 1400 p. ISBN 1584885106
• Jacobson, Nathan. Lectures in Abstract Algebra. Berlin: Springer, 1976. 217 p. v. 1. ISBN 0387901817
• Lang, Serge. Algebra. Berlin: Springer, 2002. 914 p. ISBN 038795385X
• Leon, Steven J.. Álgebra Linear com Aplicações. 4ª.ed. Rio de Janeiro: LTC, 1999. 390 p. ISBN 8521611501
• Lima, Elon Lages. Álgebra Linear. 7ª.ed. Rio de Janeiro: IMPA, 2006. 357 p. ISBN 8524400897

Ligações externas

• Linear Algebra Livro de Álgebra linear no wikilivros em inglês.
• A First Course in Linear Algebra - livro sobre álgebra linear, em língua inglesa, licenciado sob a GNU Free Documentation License.
• Linear Algebra - outra opção de livro em língua inglesa, licenciado sob a GNU Free Documentation License.
• Página do professor Reginaldo (UFMG) - contém diversos livros sobre o assunto.