Teoria de números/Imprimir
Este livro está sendo estruturado originalmente com base em notas de aula do curso de introdução a teoria de números oferecido pelo IMPA no verão de 2008. Seu conteúdo não precisa (nem deve) se limitar àquele que consta atualmente no índice. Sendo assim, a qualquer momento o livro pode ser revisto e ampliado.
Sinta-se a vontade para ler este e qualquer outro livro do projeto, melhorando-os conforme lhe for possível. Com isso estará ajudando a aumentar a qualidade geral do Wikilivros.
Se tiver dúvidas ou sugestões sobre páginas específicas, utilize as páginas de discussão correspondentes para deixar um comentário a respeito.
Ainda há muito por fazer, mas todos aqueles que contribuem acreditam estar fazendo o possível para oferecer o melhor a todos.
| Este módulo tem a seguinte tarefa pendente: Incluir no prefácio uma descrição global de quais assuntos serão tratados neste wikilivro, comentando sobre o enfoque escolhido. |
Nesta página estarão indicadas as convenções adotadas neste wikilivro, no que diz respeito a sua formatação.
Recomenda-se a leitura do mesmo, por todos que pretendem contribuir com a melhoria desde texto.
Definições
[editar | editar código-fonte]- Definição
Uma definição pode ser entendida como o texto que explica de forma precisa o significado de um conceito.
- Observações
- Geralmente um termo importante aparece pela primeira vez em uma definição.
- Devido à sua importância, é bom destacar a definição do restante do texto.
- No momento, a forma de destacar uma definição neste wikilivro é a inclusão da mesma dentro de uma região com bordas duplas, como no exemplo acima. Par isso, utilize
{{Definição}}. - O conceito que está sendo definido tem sido colocado em negrito, sendo que o texto da explicação tem sido alinhado a esquerda.
Propriedades, Teoremas
[editar | editar código-fonte]- Teorema
Sempre que uma propriedade importante dos objetos tratados no texto precisa ser destacada, isto deve ser feito em uma caixa como essa.
- Observações
- Os principais itens a ser destacados são: teoremas, proposições, corolários e pequenos lemas.
- Utilize
{{Teorema}}quando precisar destacar essas propriedades.
Demonstrações, Justificativas
[editar | editar código-fonte]| Demonstração |
|---|
| As demonstrações aparecem em quadros como esse. |
- Observações
- Utilize
{{Demonstração}}nesses casos. - Por padrão, se não for inserido qualquer texto para a demonstração, o resultado é:
| Demonstração |
|---|
| Esta demonstração é deixada a cargo do leitor. Sinta-se livre para melhorar a qualidade deste texto, incluindo-a na versão online deste material. |
Antes de mais, agradecemos à Wikipedia pela oportunidade.
Sem mais demoras: 1=1+1-1(=)1+1=1+1(=)(1^2)-(1^0)+(1^+∞)=1
Desde a Pré-História que surgiu a necessidade física ao ser humano de criar a Unidade. Certo dia,no paleolítico médio, um recolector começou a contar quantas bagas havia conseguido guardar depois daquele dia exaustivo de procura por alimento. Começou por usufruir de uma das ferramentas mais importantes na altura, o seu próprio corpo e o que a evolução lhe havia dado, nada mais nada menos do que os próprios dedos da sua mão.
|
Esta página é um esboço de matemática. Ampliando-a você ajudará a melhorar o Wikilivros. |
|
Faltam capítulos neste índice. |
Nesta página estão listados os conceitos abordados neste livro em ordem alfabética.
O nome de cada conceito possui um link para a página onde o mesmo é definido. Outras ocorrências importantes do conceito são indicadas pelos links numerados, logo após o link principal.
A teoria de números é a área da matemática em que é estudado o anel dos números inteiros.
O conjunto dos números inteiros é denotado por , sendo que:
O conjunto pode ser definido formalmente a partir do conjunto dos números naturais e estes, a partir dos axiomas de Peano. Para maiores detalhes sobre o assunto pode ser consultado o "capítulo específico" do wikilivro sobre álgebra abstrata, ou o livro de Milies & Coelho (2003).
O conjunto dos números inteiros é definido juntamente com duas operações: a adição e a multiplicação.
A estrutura aditiva dos números inteiros é trivial. Acompanhe os exemplos:
| -2 | -1 | 0 | 1 | 2 | 3 | 4 | |
Como se pode observar, qualquer número inteiro pode ser "formado aditivamente" a partir do número 1. Nesse sentido, a unidade é o "bloco básico" a partir do qual são construídos todos os números inteiros, usando-se as propriedades da operação de adição (como por exemplo a associatividade e a existência de elemento oposto).
Além disso, dado um número inteiro, sua decomposição em "blocos básicos" é essencialmente uma só. Por exemplo, se considerarmos o número 5, teremos:
No entanto, a única diferença entre duas representações do 5 é a posição dos parêntesis. Não há uma mudança significativa.
Já a estrutura multiplicativa de é muito mais sofisticada. Veja alguns exemplos:
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| bloco básico | bloco básico | bloco básico | bloco básico | bloco básico |
Como deve ter percebido, quando se trata da operação de multiplicação, não existe um único bloco básico que gere todos os outros números. Por exemplo, os números 2, 3, 5, 7 e 11 não têm como ser obtidos a partir da multiplicação de dois números inteiros (além de 1 e eles próprios), mas permitem gerar outros números: , e assim por diante. Parece razoável que todos os inteiros podem ser gerados dessa maneira, bastando encontrar os blocos básicos adequados.
Mas será que mesmo sendo necessários mais "blocos básicos" para a estrutura multiplicativa que para a aditiva, um número inteiro sempre será decomposto de forma única em tais blocos?
Como foi visto, isso é o que acontece na estrutura aditiva. No entanto, para responder (de forma afirmativa) a esta pergunta, será necessário definir o conceito de divisibilidade, e conhecer de suas algumas propriedades. Este é o conteúdo da próxima seção.
Definição de divisibilidade
[editar | editar código-fonte]- Definição
Dados os inteiros e , diz-se que " divide " e escreve-se , se existe um inteiro tal que . Alternativamente, pode ser lido como " é divisor de ", " é um fator de " ou " é múltiplo de ". Quando não se tem , escreve-se .
O conceito apresentado acima define uma relação binária no conjunto dos números inteiros: a divisibilidade.
Lembre-se que uma relação binária sobre é qualquer subconjunto do conjunto das partes de , . No caso da divisibilidade, tem-se:
Nesses termos, quando costuma-se dizer que está relacionado com escrevendo-se .
Propriedades da divisibilidade
[editar | editar código-fonte]A relação de divisibilidade possui as seguintes propriedades, para quaisquer (salvo indicação em contrário) inteiros :
1. (reflexividade) 2. e implica (transitividade) 3. e implica ou 4. e implica (linearidade) 5. e implica 6. implica (multiplicatividade) 7. e implica (lei do cancelamento) 8. ( divide todo número inteiro) 9. (todo número inteiro divide zero) 10. implica (zero só divide zero) 11. implica (os divisores de 1 são 1 e -1) 12. e implica (compatibilidade com a ordem "") 13. e implica
1. Como segue da definição que .
2. Se e , então existem tais que e , logo e portanto .
3. implica que . E se , então . Logo como não pode ser menor que e não pode ser menor que ao mesmo tempo, temos que . e também são possíveis, já que a diferença entre e é somente o sinal do quociente. O mesmo vale para e .
4. Como e temos que e com e . Multiplicando a primeira igualdade por e a segunda por , temos e . Somando membro a membro e colocando em evidência: daí como é inteiro segue por definição que .
5. Tendo e , podemos transformar e em equações: e , sendo e os quocientes das divisões. Multiplicando ambas as equações temos: . Assim, já que é o quociente da divisão (cujo resto ), temos que .
6. Adicionando fatores comuns no dividendo e divisor da equação (divisão exata), que implica em ; não altera o resultado da divisão, pois: . Como : . Assim , que implica em .
7. Como vem de (c = quociente), vem de , no qual podemos tirar da divisão, já que ele é um fator comum no dividendo e divisor de . Assim .
8. implica que . Assim .
9. implica que . Logo .
10. pode ser transformado em . Como não existe divisão por 0 (já que tendo e não existe número que multiplicado por 0 dê x </math>), o único número que pode estar no dividendo é 0. Logo implica em .
11. implica que . Como os divisores de , temos que .
12. Como e podemos escrever com . Assim, e .
13. Transformando em equação, temos . Utilizando-se da propriedade da divisão: tendo podemos inverter o quociente e o divisor (já que , e os fatores podem ser reordenados sem mudar o resultado) para termos: . Assim: e implicam em .- Observações
- A terceira propriedade seria chamada de anti-simetria, se não fosse necessário considerar o caso "". Quando são considerados apenas os números não-negativos (os elementos de ) a conclusão é apenas "", e as propriedades de 1 a 3 fazem da divisibilidade uma relação de ordem parcial sobre . No entanto, essa não é uma ordem total, pois nem todo par de elementos em é comparável, ou seja, existem inteiros não negativos e , para os quais não se tem nem .
- Frequentemente é mais prático trabalhar apenas com o conjunto dos números naturais (o subconjunto dos inteiros não-negativos ) ou com os números naturais não nulos (os inteiros positivos ).
- As propriedades 1 e 8 garantem que todo número inteiro não negativo , diferente de , possui ao menos dois divisores, chamados de divisores triviais: e . Os números que possuem somente estes divisores são de grande interesse na teoria de números, e serão estudados no próximo capítulo.
Critérios de divisibilidade no sistema de numeração decimal
[editar | editar código-fonte]Nas aulas de matemática do ensino fundamental, é possível que você tenha aprendido algumas regras (ou critérios) para saber rapidamente se um certo número é divisível por outro. Por exemplo, você identifica rapidamente que um número é par quando nota que o seu último dígito é par, assim como reconhece de imediato os múltiplos de 5, pois sabe que o seu dígito das unidades é sempre 0 ou 5.
O que talvez você não saiba é que podem ser deduzidos critérios de divisibilidade para vários outros números, senão todos, embora nem sempre tais regras sejam simples e fáceis de memorizar. Uma listagem das regras mais populares é apresentada na próxima tabela. Note que as regras descritas transformam um certo número em outro, geralmente menor, que preserva a divisibilidade pelo divisor em questão. Além disso, sempre que não fica claro se um número é múltiplo de certo divisor, a mesma regra pode ser aplicada novamente ao resultado já obtido, até que se torne evidente se determinado resultado é ou não divisível pelo divisor em questão.
| Um número é divisível por... |
quando... | Exemplos |
|---|---|---|
| 1 | sempre! | Qualquer número inteiro é divisível por 1. |
| 2 | seu dígito das unidades é par (ou seja, 0, 2, 4, 6, ou 8). | 1 294 é par[1], pois 4 é par. |
| 3 | é divisível por 3 a soma dos seus dígitos.[2] | 405 é divisível por 3, pois 4 + 0 + 5 = 9, que é múltiplo de 3. |
| 4 | é divisível por 4 o dígito das unidades somado com o dobro do dígito das dezenas. | 5 096 é múltiplo de 4, pois 6 + (2 × 9) = 24 que é múltiplo de 4 |
| é divisível por 4 o número formado pelos dois últimos dígitos. | 70 841 não é divisível por 4, pois 41 não é. | |
| 5 | o dígito das unidades é 0 ou 5. | 123 456 7890 é divisível por 5, já que seu último dígito é 0. |
| 6 | é divisível por 2 e por 3. | 24 é divisível por 6, já que seu é múltiplo de 2 e de 3. |
| é divisível por 6 a soma do dígito das unidades com o quádruplo da soma dos demais dígitos. | 12 348 é divisível por 6, pois (1 + 2 + 3 + 4) × 4 + 8 = 48 | |
| 7 | ||
| é divisível por 7 a diferença entre o número formado ao desconsiderar o último dígito e o dobro deste dígito. | 364 é divisível por 7, pois 36 − (4 x 2) = 28. | |
| 8 | ||
| o dígito das centenas é ímpar e o número formado pelos dois últimos dígitos, somado com 4 é divisível por 8. | 12 352, é múltiplo de 8, já que 3 é ímpar e 52 + 4 = 56 = 7 x 8. | |
| é divisível por 8 a soma do último dígito com o dobro do número formado pelos demais. | 136 é divisível por 8, uma vez que (13 × 2) + 6 = 32. | |
| 9 | é divisível por 9 a soma dos seus dígitos.[3] | 3 753 é múltiplo de 9, pois 3 + 7 + 5 + 3 = 18 e 1 + 8 = 9 |
| 10 | o último dígito é 0. | 135790 é múltiplo de 10, pois seu último dígito é 0. |
| 11 | ||
| é divisível por 11 a soma alternada dos seus dígitos. | 918 082 é múltiplo de 11, pois 9 - 1 + 8 - 0 + 8 - 2 = 22 = 2 x 11. | |
| é múltiplo de 11 a soma dos números formados pelos blocos de dois dígitos (da direita para a esquerda). | 627 é múltiplo de 11, pois 6 + 27 = 33 = 3 x 11. | |
| é múltiplo de 11 a diferença entre o número formado ao desconsiderar o último dígito e o último dígito. | 627 é múltiplo de 11, já que 62 - 7 = 55 = 5 x 11.. |
Por que esses critérios funcionam?
[editar | editar código-fonte]Diante de tantas regras, é natural não acreditar de imediato que elas sejam todas infalíveis. Você já deve ter feito (ou ouvido alguém fazer) pelo menos uma pergunta desse tipo:
- Quem disse que esses macetes funcionam sempre?
- Por acaso alguém já testou algum deles para todos os números, e viu que nunca falham?
- Quem é que impôs essas regras?
- É possível encontrar um critério para os números que não estão na tabela?
Antes de responder a essas e outras perguntas do gênero, é interessante apresentar um resultado fundamental da teoria de números. O enunciado não deve parecer uma grande novidade, pois formaliza o tão conhecido algoritmo de divisão, aquele processo utilizado ao dividir dois números manualmente. Se estiver um pouco "enferrujado", experimente calcular o resultado da divisão de 39629376 por 321, para relembrar as suas primeiras aulas de matemática...
Algoritmo da divisão (de Euclides)
[editar | editar código-fonte]- Teorema
Se e são números inteiros, e , então existe um único par de números inteiros e , tais que:
- , com
Uma formulação alternativa é a seguinte:
Dados os números inteiros e , ou é múltiplo de ou está entre dois múltiplos consecutivos de .
| Demonstração |
|---|
| Considere inicialmente que .
Se , então (pois para tem-se ). Logo, pelo princípio da boa ordenação, possui um menor elemento . Como , segue que , para algum inteiro , e . Suponha que . Neste caso, segue que .
Por outro lado, se , então o algoritmo pode ser aplicado a e (que não é negativo), obtendo:
Por outro lado, como o valor de cada resto está entre e , sua diferença também está. Isto significa que: Logo, Mas o único elemento de com módulo menor que é o . Assim, implica . Consequentemente, de se conclui que , que equivale a , pois .
|
Um último passo antes de apresentar a justificativa formal para os critérios de divisibilidade mostrados anteriormente é entender como funciona o sistema de numeração decimal.
Sistemas de numeração
[editar | editar código-fonte]Conforme é ensinado nos primeiros anos de escola, um número como 726 representa a soma de 7 centenas com 2 dezenas e 6 unidades, ou seja,
Em geral, cada número inteiro não negativo possui uma única representação decimal . Este é um resultado de extrema utilidade no cotidiano, pois é graças a tal sistema de numeração que estão a disposição algoritmos tão simples para a realização de adições, subtrações, multiplicações e divisões. Ou você é capaz de se imaginar realizando uma divisão de 646 por 38 utilizando o sistema de numeração inventado pelos romanos? (Experimente: DCXLVI dividido por XXXVIII é igual a...)
Dada a importância do sistema de numeração decimal, é justo enunciar e justificar precisamente o seu funcionamento. Isso é feito no próximo teorema, que garante a existência de representações posicionais em qualquer base, não apenas na base 10.
- Teorema
Dado um numero inteiro (chamado de base), maior do que a unidade, cada inteiro positivo pode ser escrito de uma única maneira como
Utilizando o algoritmo da divisão é possível obter cada dígito de uma tal representação, um após o outro, começando pelo dígito das unidades. De fato, ao dividir o número em questão pelo valor da base, consegue-se:
Fazendo o mesmo com , resulta:
Repetindo o procedimento com cada quociente , será construída uma sequência decrescente:
Certamente algum termo da sequência deve ser igual a unidade, pois todos são números inteiros e nenhum deles é negativo. Então considere que , ou seja, que o algoritmo da divisão fornece . Neste ponto o processo pode ser interrompido, e nota-se que:
Observações
[editar | editar código-fonte]- Quando a base não é 10, é comum usar a notação para explicitar esse fato.
- Os sistemas que utilizam a base 2 (binário), a base 8 (octal) e a base 16 (hexadecimal) são particularmente úteis na informática e na eletrônica digital.
- O sistema de numeração com base 60 (sexagesimal) foi inventado pelos Sumérios, e ainda é utilizado para a contagem de minutos e segundos, tanto para indicar períodos de tempo quanto para medir ângulos.
Exemplos
[editar | editar código-fonte]De posse dessas informações, já é possível demonstrar a validade dos critérios de divisibilidade dados pela tabela anterior. Nos próximos exemplos serão demonstrados alguns desses critérios. Os demais são deixados como exercício para o leitor.
Divisibilidade por 2
[editar | editar código-fonte]- Proposição
Um inteiro não negativo é par, e somente se, o dígito das unidades é par.
| Demonstração |
|---|
| Considere um número inteiro positivo cuja representação decimal é . Para mostrar que se, e somente se, , note que:
e em geral: Portanto: Assim,
Deste modo, se , então . Reciprocamente, se tem-se .
|
Divisibilidade por 3
[editar | editar código-fonte]- Proposição
Um inteiro não negativo é múltiplo de 3 se, e somente se, a soma de seus dígitos é múltiplo de 3.
| Demonstração |
|---|
| Seja um número inteiro positivo. Como no exemplo anterior, o principal é considerar as potências de 10 e os restos de suas divisões por 3.
Primeiramente, note que: onde é o número que possui todos os seus dígitos iguais a 3. Esta última igualdade é devida à fórmula clássica para a soma dos primeiros termos de uma progressão geométrica). Substituindo essas potências de 10, obtem-se: ou seja,
Deste modo, se , então . Analogamente, se tem-se . |
Divisibilidade por 11
[editar | editar código-fonte]- Proposição
Um inteiro não negativo é divisível por 11 se, e somente se, a soma alternada dos seus dígitos é divisível por 11.
| Demonstração |
|---|
| Como antes, considere um número inteiro positivo. Pode-se proceder como antes para obter o resultado. Primeiramente, observe a relação entre as primeiras potências de 10 e o número 11:
É razoável esperar que o padrão continue, ou seja, que nas potências pares se tenha para algum inteiro , e nas potências ímpares se tenha para algum inteiro . No entanto, como a intuição as vezes falha (o próprio Fermat foi vítima de sua intuição, se enganando ao afirmar que todo número da forma é primo), é necessário provar que o padrão se repete, qualquer que seja o expoente. Em símbolos, é preciso mostrar que:
Para tal usaremos o binómio de Newton: ou seja, onde Uma vez que o padrão está justificado, o raciocínio é o mesmo do caso anterior: ou seja,
Deste modo, se , então . Analogamente, se tem-se .
|
Exercícios
[editar | editar código-fonte]- Justifique a validade de cada uma das propriedades da divisibilidade apresentadas no texto.
Notas
[editar | editar código-fonte]- ↑ Veja a fatoração de 1294 e outras informações sobre este número no Wolfram Alpha (em inglês).
- ↑ Conforme diversos livros
- ↑ Conforme diversos livros
Um pouco de história
 Os números primos são conhecidos pela humanidade há muito tempo. No papiro Rhindi, por exemplo, há indícios de que o antigo povo egípcio já possuía algum conhecimento sobre esse tipo de números. No entanto, os registros mais antigos de um estudo explícito sobre números primos é devido aos gregos. Os Elementos de Euclides (cerca de 300 aC), contém teoremas importantes sobre números primos, incluindo a demonstração de sua infinitude o teorema fundamental da aritmética. Euclides também mostrou como construir um número perfeito a partir de um primo de Mersenne. Ao grego Eratóstenes, atribui-se um método simples para o cálculo de números primos, conhecido atualmente como crivo de Eratóstenes. Por outro lado, nos tempos atuais, os grandes números primos são encontrados por computadores, através de testes de primalidade mais sofisticados, como por exemplo o teste de primalidade AKS. Neste capítulo será definido o que são esses números primos, e serão apresentados os principais resultados acerca destes números. |
Definição de número primo
[editar | editar código-fonte]- Definição
Um número primo é um número natural que tem exatamente dois divisores positivos (distintos). Um número que não é primo é chamado de composto.
Como já foi observado no capítulo anterior, o fato da divisibilidade ser reflexiva (propriedade 1) e que é divisor de qualquer número inteiro (propriedade 8) garantem que todo número inteiro diferente de e possui pelo menos dois divisores: e . Com isso em mente, alguém poderia se perguntar:
- O que os números primos têm de tão especial, já que todos os números inteiros têm ao menos dois divisores?
É essencial notar que a definição acima exige que um número possua exatamente dois divisores positivos, antes de poder ser chamado de número primo. Assim, a definição exclui automaticamente o número da lista de números primos, pois ele possui um único divisor positivo: o próprio 1. Além disso, seria redundante dizer na própria definição que um número é primo somente se os seus únicos divisores são ele mesmo e a unidade, pois isso decorre da exigência de que tenha apenas dois divisores positivos.
Agora é possível explicar melhor a "decomposição em blocos básicos" apresentada no início desse texto.
Primeiramente, observe como os elementos de estão "ordenados" pela divisibilidade na figura a seguir:
No que diz respeito a multiplicação, será mostrado que todo número inteiro pode ser decomposto em um produto de números primos. Ou seja, os números primos são realmente "blocos básicos" que permitem a construção de todos os outros números inteiros, a partir de multiplicações.
Este resultado, de grande importância é sintetizado no próximo teorema.
Teorema da existência de fatoração
[editar | editar código-fonte]- Teorema
Todo número inteiro positivo maior do que um tem decomposição em fatores primos.
| Demonstração |
|---|
| Dado um número inteiro , vamos mostrar por indução que , com cada sendo um número primo.
De fato, para , o teorema é válido, pois basta tomar . Se , e for primo, a afirmação é obviamente verdadeira, pois é suficiente escolher . Considere então que é composto, e que a hipótese de indução é que todo número menor que admite decomposição em fatores primos. Logo, existem inteiros e tais que . Além disso, e são menores que . Pela hipótese de indução, tem-se
com cada e cada sendo um número primo, donde segue que: Assim, basta renomear os primos e como , e tem-se o teorema. |
Exemplos
[editar | editar código-fonte]Com o auxílio de um computador, e algum software para computação algébrica, verifica-se ques são verdadeiras as seguintes igualdades:
e ainda:
Na página Factorization using the Elliptic Curve Method está disponível um pequeno aplicativo que determina a fatoração de um número ou expressão numérica. O aplicativo foi escrito em Java, e não precisa ser baixado para poder ser executado.
Nos próximos exemplos, são apresentados alguns sub-conjuntos de onde a operação de multiplicação continua (bem) definida. Esses conjuntos, assim como o conjunto dos números inteiros, possuem "blocos básicos" que permitem gerar todos os seus elementos a partir da multiplicação. No entanto, os exemplos servirão como motivação para o Teorema fundamental da artimética que será demosntrado posteriormente. Esse teorema garante que um número inteiro só possui uma decomposição em fatores primos, ou seja, se Carlos e Joana encontrarem duas fatorações em primos para um certo número inteiro , então ambos encontraram os mesmos números primos, cada um aparecendo a mesma quantidade de vezes nas duas fatorações.
Ao contrário do que se possa esperar, essa propriedade não é uma consequência imediata das definições de divisibilidade e de números primos. Na verdade, a unicidade só é válida porque possui além de uma estrutura multiplicativa, uma estrutura aditiva com "boas propriedades". É a partir das propriedades de ambas as estruturas, que o teorema poderá ser demonstrado.
Os próximos exemplos servirão, portanto, para mostrar que em conjuntos onde se tem apenas uma estrutura multiplicativa, a decomposição em fatores "primos" (será dado um novo significado ao termo) pode não ser única.
O conjunto dos números pares positivos
[editar | editar código-fonte]Considere o conjunto .
Quem são os elementos que permitem "gerar" todos os demais através da multiplicação? Acompanhe:
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | ... | |
| fatoração de | 2 | 6 | 10 | 14 | 18 | ... |
Observe que 6 não pode ser escrito como o produto de outros dois números pares, pois estes teriam que ser necessariamente menores que 6. Assim, é rápido verificar (fazendo alguns poucos testes) que tal fatoração não é possível.
Nesse sentido, o número 6 (assim como o 2, o 10, o 14 e o 18) é um elemento irredutível de . De modo geral, um elemento é irredutível se não puder ser decomposto em um produto. Os elementos que não são irredutíveis, são naturalmente chamados de redutíveis.
Observe que se é um elemento redutível de , então , ou seja, todo elemento redutível é um múltiplo de 4.
Os elementos irredutíveis de serão os "blocos básicos" a partir dos quais poderão ser gerados todos os outros números pares.
Da mesma forma como foi demonstrado que todo número inteiro possui uma decomposição em fatores primos, pode-se provar que todo elemento de possui uma decomposição em fatores irredutíveis.
| Prova |
|---|
| Esta prova é deixada a cargo do leitor. Sinta-se livre para melhorar a qualidade deste texto, incluindo-a na versão online deste material. |
Uma última consideração a respeito do conjunto (e que justifica a escolha do mesmo para este exemplo), é que embora todos os seus elementos admitam uma fatoração em irredutíveis, pode haver mais de uma decomposição para um mesmo número. Veja:
E como se verifica facilmente, os números acima são todos irredutíveis em .
Essa característica sugere que se os números inteiros possuem uma única fatoração em primos, isso se deve a alguma outra propriedade de , além de sua estrutura multiplicativa.
O monóide de Hilbert
[editar | editar código-fonte]Seja .
Verifica-se facilmente que a multiplicação de elementos de possui as seguintes propriedades:
- , quaisquer que sejam ;
- , para quaisquer ;
- O elemento neutro da multiplicação, o número inteiro 1, está em .
Este conjunto é conhecido como o monóide de Hilbert.
A propriedade 1 decorre dos seguintes cálculos: Se e então
Novamente, tem-se a decomposição em fatores irredutíveis (fatores que não são produto de outros elementos em ). Acompanhe a fatoração de alguns elementos de :
| 1 | 5 | 9 | 13 | 17 | 21 | 25 | 29 | ... | 45 | ... | 65 | ... | 117 | ... | |
| fatoração de | 1 | 5 | 9 | 13 | 17 | 21 | 29 | ... | ... | ... | ... |
Outros monóides
[editar | editar código-fonte]É possível obter outros exemplos similares procedendo de forma análoga com os conjuntos , e em alguns casos com (para quais ainda funciona?). Também o conjunto possui essas propriedades.
Teorema de Euclides
[editar | editar código-fonte]- Teorema
Existe uma infinidade de números primos.
Demonstração de Euclides
[editar | editar código-fonte]| Demonstração |
|---|
| Considere um conjunto finito de números primos, contendo uma quantidade arbitrária de elementos. Denote tal conjunto por .
Seja . Como , então tem algum fator primo , ou seja, . Se , seria verdade que , devido a linearidade da divisibilidade. Mas nenhum primo divide 1, então . Assim, mostrou-se que não importa quantos elementos tenha um certo conjunto de números primos, sempre existirá um outro número primo que não está em , ou seja, existe uma infinidade de números primos! |
Exemplos
[editar | editar código-fonte]Se o conjunto que aparece na demonstração do teorema for constituído dos primeiros números primos, então as fatorações de para alguns valores de são as seguintes:
| Fatoração de | Tipo | ||
|---|---|---|---|
| primo | |||
| primo | |||
| primo | |||
| primo | |||
| primo | |||
| composto | |||
| composto |
A demonstração acima pode ser adaptada para mostrar que o monóide de Hilbert possui infinitos elementos irredutíveis. Observe:
| Demonstração |
|---|
| Se são elementos irredutíveis de , então é também um elemento de (por quê?), e portanto possui decomposição em fatores irredutíveis em .
Seja um dos fatores que aparecem na decomposição de . Então , para , caso contrário (pelo mesmo motivo de antes). Logo existem infinitos números irredutíveis em . |
- Observação
Não serve escolher . Por que?
Demonstração de Hermite
[editar | editar código-fonte]Esta demonstração, assim como algumas outras, é uma variante daquela dada por Euclides. Acompanhe:
| Demonstração |
|---|
| Para cada número natural , defina-se .
Como qualquer outro número natural, possui algum fator primo . No entanto, este fator não pode ser divisor de qualquer número menor ou igual a , pois neste caso, dividiria também , e consequentemente seria divisor de . Portanto, tem que ser maior do que . Resumindo, dado qualquer inteiro positivo , existe um número primo que é maior do que , ou seja, o conjunto dos números primos é infinito. |
Exemplos
[editar | editar código-fonte]Uma tabela como a anterior pode ser feita para os números . Neste caso, tem-se:
| Fatoração de | Tipo | ||
|---|---|---|---|
| primo | |||
| primo | |||
| primo | |||
| composto | |||
| composto | |||
| ... | ... | ... | ... |
| (bem grande!) | ... | primo |
Um fato curioso é que a última linha da tabela corresponde ao maior número primo da forma para valores de até 35500.
Demonstração de Saidak
[editar | editar código-fonte]| Demonstração |
|---|
| Esta demonstração foi publicada recentemente pelo pesquisador Filip Saidak, em seu artigo A new proof of Euclid’s theorem de 2006. A prova consiste no seguinte:
Forma-se uma sequência crescente de números , de tal modo que cada termo tenha pelo menos fatores primos. Dessa forma, inevitavelmente, conclúi-se que existem infinitos números primos. A sequência inicia com . Como e não têm divisores em comum, o produto possui ao menos 2 divisores primos. Do mesmo modo, e não têm fatores em comum, logo possui ao menos 3 fatores primos. O processo pode continuar indefinidamente, definindo-se sempre , e cada terá no mínimo k fatores primos (verifique isto por indução!). |
Exemplos
[editar | editar código-fonte]Tomando , obtem-se a seguinte tabela:
| Fatoração de | ||
|---|---|---|
Teorema fundamental da aritmética
[editar | editar código-fonte]- Teorema
A decomposição de um número inteiro em fatores primos é única, exceto pela ordem. Em símbolos: Se , e cada e todo é um número primo, então e para cada tem-se , para alguma permutação .
Na demonstração deste resultado será assumido que é válido um outro teorema, cuja justificativa só será apresentada no próximo capítulo. Trata-se de uma propriedade bastante elementar, que já era conhecida por Euclides (alguns anos A.C):
- Teorema
Se um número primo divide o produto de dois números inteiros, então ele é divisor de um dos dois.
(I)
- Observação
- Em Álgebra a propriedade mencionada é usada para definir "primo" e em geral, a "irredutibilidade" (definida nos exemplos do primeiro capítulo) não coincide com a noção de "primalidade".
- A estrutura aditiva de será crucial na demonstração desta propriedade e consequentemente, do teorema fundamental da aritmética.
Demonstração do teorema fundamental da aritmética
[editar | editar código-fonte]| Demonstração |
|---|
| A prova será feita por indução.
Se , o resultado é imediato, então considere que o mesmo vale para todo número inteiro menor que . Supondo que existem duas decomposições para o inteiro , ou seja, , segue que algum é múltiplo de . Como a ordem dos fatores não é importante, pode-se supor que . Neste caso, seque que , pois e os únicos divisores de são e ele próprio. Logo,
Certamente , então pela hipótese de indução, possui uma fatoração única, donde e , para cada índice. Assim, a fatoração de é única. |
Corolário
[editar | editar código-fonte]- Corolário
Todo pode ser escrito como , com e .
Esta é chamada de forma padrão da decomposição em fatores primos.
Outra forma de escrita é
- , com , exceto para uma quantidade finita de 's.
A constatação da verdade dessas afirmações é elementar.
Aplicação
[editar | editar código-fonte]A partir dessa notação pode-se definir uma função escolhendo . Verifica-se que a função acima definida goza das seguintes propriedades:
Essa função oferece uma forma "elegante" de se fazer certas demonstrações. Por exemplo, a irracionalidade de é provada assim:
| Demonstração |
|---|
| Se fosse racional, poderia ser escrito como , sendo que , e .
Neste caso, seria verdade que , ou seja, . Aplicando a função em ambos os membros, segue que No entanto, essa igualdade não é possível, pois o primeiro membro é um número par, e o último é ímpar. Logo, só pode ser irracional. |
Uma equivalência
[editar | editar código-fonte]Como foi mostrado, se a propriedade (I) for válida, tem-se a validade do teorema fundamental da aritmética. Na verdade, as duas proposições são equivalentes.
Lembre-se que para garantir uma equivalência lógica (para mais informações, consulte algumas seções do wikilivro sobre lógica), é preciso verificar duas implicações, uma das quais já foi demonstrada neste capítulo. Resta ainda verificar o seguinte: ao supor a validade do teorema fundamental da aritmética, pode ser provada a propriedade (I)?
A resposta é afirmativa, e o motivo você encontrará nesta seção. Veja:
| Demonstração |
|---|
| Suponha que . Então, pela definição de divisibilidade, existe algum número inteiro tal que .
Mas e possuem decomposição em fatores primos, então:
Logo, , ou seja, precisa ser um dos 's ou um dos 's. No primeiro caso, conclui-se que , e no segundo . |
Exercícios
[editar | editar código-fonte]- Demonstre os seguintes fatos:
- Se (com ) for um número primo maior do que , então ou .
- O produto de dois elementos quaisquer do conjunto é ainda um elemento deste conjunto.
- O conjunto possui uma infinidade de números primos.
Por enquanto, há poucos exercícios sobre este capítulo. O leitor está convidado a adicionar mais exercícios nesta seção, para ajudar a melhorar o texto.
No capítulo anterior, foi demonstrado o teorema fundamental da aritmética. No entanto, a prova apresentada, utilizou-se de um resultado cuja prova apresentaremos neste capítulo. Para tanto, será preciso definir o conceito de máximo divisor comum entre dois números inteiros.
Este é o conteúdo da próxima seção.
Divisores comuns
[editar | editar código-fonte]- Definição
Um divisor comum de e é um número inteiro que é divisor tanto de quanto de .
Exemplos
[editar | editar código-fonte]Quem são os divisores comuns de a e b?
[editar | editar código-fonte]O conjunto formado pelos divisores comuns de e será denotado por .
No primeiro capítulo, mostrou-se que o número é divisor de qualquer número inteiro. Em particular, se forem escolhidos números e , certamente será um divisor comum de ambos.
Logo, o conjunto é não vazio, pois .
O maior dos divisores comuns
[editar | editar código-fonte]Se e for um divisor comum de e de , então . Logo o conjunto é limitado superiormente e deve ter um elemento máximo, ou seja, existe um divisor comum de e maior que todos os demais. Analogamente, para , o conjunto também tem um elemento máximo. O único caso que não é limitado superiormente é o conjunto , já que zero é múltiplo de qualquer inteiro não-nulo.
Isso motiva a próxima definição.
Definição de MDC
[editar | editar código-fonte]- Definição
O máximo divisor comum (abreviadamente MDC) entre dois números inteiros e , em que pelo menos um deles não é zero, é o maior elemento do conjunto , e será denotado por , ou simplesmente .
Quando o conjunto possui apenas um elemento positivo, ou seja, quando , os números e são ditos primos entre si, relativamente primos ou simplesmente co-primos.
| Este módulo tem a seguinte tarefa pendente: Unificar a notação utilizada ao longo do livro para denotar o MDC. Pode ser mais adequado utilizar sempre mdc(a,b), em vez de (a,b), para evitar confusões. Em caso de dúvida, pode-se discutir o assunto. |
Exemplo
[editar | editar código-fonte]Qual é o máximo divisor comum entre e ?
Considerando que os divisores de são os elementos do conjunto e que os divisores de formam o conjunto , tem-se que , cujo maior elemento é . Portanto, .
Embora ainda não tenha sido explicado como encontrar o máximo divisor comum de dois números inteiros (isso será feito mais adiante), mostra-se que ele é um dos elementos do conjunto . Este resultado é um teorema surpreendente, pois relaciona a estrutura multiplicativa do conjunto dos números inteiros que foi estudada até agora, com sua estrutura aditiva:
Teorema de Bézout
[editar | editar código-fonte]- Teorema
Se , então existem inteiros e tais que .
O resultado também é conhecido como identidade de Bézout.
Antes de apresentar qualquer justificativa (construtiva ou puramente algébrica) dessa identidade, serão mostradas suas consequências imediatas mais importantes.
Corolário
[editar | editar código-fonte]- Corolário
Se e então .
| Demonstração |
|---|
Pelo teorema anterior, o máximo divisor comum entre e pode ser escrito como:
Multiplicando cada membro da equação anterior por , obtem-se . Claramente, divide cada parcela desta soma. Consequentemente deve dividir . |
Com essa propriedade, devida a Euclides de Alexandria, já é possível demonstrar o teorema que ficou pendente no capítulo anterior:
Propriedade fundamental dos primos
[editar | editar código-fonte]- Teorema
Se um número primo divide o produto de dois números inteiros, então ele é divisor de um dos dois.
| Demonstração |
|---|
| Sejam e um número primo que divide o produto .
Será provado que se não divide , então deve necessariamente dividir . De fato, como é primo, o conjunto de seus divisores é . Além disso, , logo não pode ser um divisor comum de e . Segue que . De acordo com o corolário acima, isso implica que divide . |
Demonstração do teorema de Bézout
[editar | editar código-fonte]Uma observação crucial para a demonstração do teorema de Bézout é que, para quaisquer números inteiros , tem-se a igualdade .
De fato, para que tal propriedade se verifique, é suficiente que os conjuntos e sejam iguais. Isso é verdade, pois:
- Se um deles está definido, então o outro também está. De fato, para b diferente de zero ambos conjuntos são definidos; para b igual a zero temos que a deve ser diferente de zero, e os dois conjuntos são iguais.
- Se , então e .
Donde, .
Assim, .
- Reciprocamente, se , então e . Logo, deve dividir a soma:
- ,
ou seja, .
Outra propriedade do máximo divisor comum é a seguinte:
Por causa dela, pode ser suposto que , e obter a demonstração:
| Demonstração |
|---|
| A prova será feita por indução em .
Obviamente, se , tem-se , e a propriedade é válida pois sempre que tem-se: Logo, pode ser suposto que (e portanto, ). Será tomada como hipótese de indução que: os pares de números inteiros , cuja soma seja menor que , têm . Como , e somado com é menor que , a hipótese de indução garante que . Então: |
Como toda prova por indução, a demonstração anterior fornece um algoritmo. No caso, trata-se de um procedimento para o cálculo de :
Dados de entrada Os inteiros e . Saída . Procedimento * Se , então ; * Se , então ; * Senão
Exemplos numéricos
[editar | editar código-fonte]Usando o procedimento sugerido, pode-se calcular facilmente. Acompanhe:
No entanto, quando se tem bem maior que , a igualdade mais utilizada será .
Por exemplo, se e as etapas serão:
Neste caso, parece razoável subtrair de tantas vezes quanto for possível, em uma única etapa:
Em geral, será buscado um valor tal que , pois assim a igualdade (que é sempre verdadeira, para qualquer valor inteiro de ) reduz o cálculo de a um caso bem mais simples.
A existência de um número , satisfazendo ambas as desigualdades é garantida pelo algoritmo da divisão apresentado em um capítulo anterior. Se precisar relembrar os detalhes, consulte a seção "Algoritmo da divisão (de Euclides)".
De posse deste algoritmo, pode-se fazer uma melhoria no algoritmo sugerido anteriormente para o cálculo do MDC.
Algoritmo de Euclides para o MDC
[editar | editar código-fonte]| Este módulo tem a seguinte tarefa pendente: Adicionar informações históricas sobre o algoritmo e também uma referência às aplicações atuais em música, descrita nos artigos do Brun, e do Toussaint.
Consulte a Bibliografia |
- Teorema
Dados , com , verifique se . Em caso afirmativo, o máximo divisor comum é o próprio . Caso contrário, repita o processo usando e o resto da divisão de por . Simbolicamente: Dados de entrada Os inteiros e . Saída . Procedimento * Se , então ; * Se , então ; * Senão , onde
Observe que esta é simplesmente uma generalização do algoritmo apresentado logo após a demonstração do teorema de Bézout.
É preciso verificar que o algoritmo irá parar, e ainda mais importante, que fornecerá a resposta correta.
Considere e , e a seguinte sequência de igualdades (obtidas pelo algoritmo da divisão):
Juntando as desigualdades anteriores, tem-se uma sequência decrescente de números não negativos:
No entanto, só existe uma quantidade finita de números positivos menores que . Logo, depois de algum resto , tem-se , ou seja:
É nesse ponto que o algoritmo para: quando o resto . Segundo o enunciado, o resultado fornecido será então .
Será que este é realmente o valor de ?
A resposta é sim, pois .
Logo, obtem-se sucessivamente:
Portanto o valor fornecido pelo algoritmo corresponde a , e foi obtido através de exatamente divisões.
Exemplo numérico
[editar | editar código-fonte]Quanto é ?
Aplicando o processo usado na demonstração do algoritmo de Euclides para o MDC, tem-se:
Logo, .
Para que não seja preciso explicitar cada uma das igualdades, pode-se dispor as informações de cada etapa em uma tabela como a seguinte:
quociente 1 1 2 30 18 12 6 Resto 12 6 0
É importante notar que, embora os quocientes apareçam indicados, o interesse está no valor dos restos.
Para obter automaticamente todas as etapas da aplicação do algoritmo de Euclides a outros pares de números inteiros, pode-se utilizar este recurso on-line, desenvolvido em javascript.
Interpretação matricial
[editar | editar código-fonte]Na demonstração de que o algoritmo de Euclides funciona, aparecem várias igualdades da forma:
O índice indica que esta é a -ésima divisão efetuada no algoritmo.
Cada uma dessas equações é uma equação de diferenças de segunda ordem, em que cada termo é descrito em função de dois anteriores. No caso, cada resto depende dos próximos dois restos, e reciprocamente, cada resto depende dos dois anteriores.
Tal relação de recorrência pode também ser expressa como:
- , sempre que
Com essa notação, os cálculos que aparecem no algoritmo de Euclides para o MDC tornam-se mais sucintos. Por exemplo:
Para facilitar ainda mais a escrita, pode-se adotar a seguinte convenção:
Se o cálculo anterior for efetuado para todas as etapas do algoritmo, o resultado final será:
- , sendo que .
Perceba que assim não há uma confusão tão grande com os índices dos sucessivos quocientes e restos.
Como a matriz é um produto de matrizes com entradas inteiras e não-negativas, nenhuma de suas entradas deverá ser negativa. Assim, é possível escrever da seguinte forma:
- , com
Disso se conclui que
Escrevendo , tem-se
- , pois cada matriz tem determinante igual a .
Logo, a matriz é invertível e . Esta última igualdade se justifica pois .
Dessas considerações, resulta que:
Fazendo o produto, e igualando cada componente, conclui-se que:
A primeira destas equações corresponde ao teorema de Bézout, com e . Já a segunda, implica em . Esse valor coincide com o conhecido mínimo múltiplo comum entre e , definido a seguir:
- Definição
O mínimo múltiplo comum dos inteiros e , , é o menor elemento positivo do conjunto
Segundo o comentário que precede esta definição, tem-se:
| Justificativa |
|---|
| Fica a cargo do leitor justificar este fato. Sinta-se livre para melhorar a qualidade deste texto, incluindo a justificativa na versão online deste material. |
Exemplificando
[editar | editar código-fonte]Anteriormente foi visto que:
Utilizando esses valores, segue que:
- .
Para este exemplo, a matriz inversa é
Logo,
- , ou seja
Note que, quando são positivos, a expressão deve ter exatamente um dos valores menor que zero, para que a combinação linear de não seja maior que qualquer um deles.
Considere uma outra situação: como encontrar o mínimo múltiplo comum entre e ?
Primeiramente, pelo algoritmo de Euclides tem-se:
Logo
Daí tem-se que
Uma demonstração alternativa do teorema de Bézout
[editar | editar código-fonte]Agora será apresentada uma prova não construtiva do teorema de Bézout. Isso significa que, embora a mesma assegure a validade do teorema, ela não fornece um método para a obtenção do MDC (ao contrário do que foi feito anteriormente).
Além disso, são utilizados alguns conceitos que certamente são conhecidos por aqueles que possuem conhecimentos básicos de álgebra. Se este não for o seu caso, você poderá pular esta seção, e não haverá prejuizo na leitura do restante deste livro.
| Demonstração |
|---|
| Sendo números inteiros, considere .
Então, é um subgrupo aditivo de (um ideal), ou seja, possui as seguintes propriedades:
De fato, se então: com . Então: Mas todo subgrupo (aditivo?) de é escrito como , com , pois:
Para provar que se tem , escreva (isso é possível, já que ). Observe que: Então, tem-se , ou seja, é divisor de . Mas é o maior divisor porque, dado qualquer outro divisor , tem-se Logo, , ou seja, . |
Exercícios
[editar | editar código-fonte]- O algoritmo da divisão estabelece que dados os inteiros , existem inteiros tais que , com . Utilize uma calculadora comum (e apenas as quatro operações elementares) para obter os valores de correspondentes a alguns pares de inteiros .
- Dados a e b, determine o valor de mdc(a,b) e números inteiros x, y tais que d = xa + yb, para os seguintes valores de a e b:
- a = 299 e b = 161
- a = 435 e b = 232
- a = 101 e b = 33
- a = 145 e b = 48
Ver também
[editar | editar código-fonte]Wikipedia
[editar | editar código-fonte]Livros em português
[editar | editar código-fonte]- Coutinho, Severino Coullier. Números inteiros e criptografia RSA. Rio de Janeiro: IMPA, 2005. 226 p. ISBN 8524401249
- Neste livro são tratados os tópicos de teoria de números que são essenciais para a compreensão do método de criptografia RSA. A forma de exposição do conteúdo procura evitar o padrão "Definição, Teorema, Demonstração", que é usado em muitos livros de matemática.
- Hefez, Abramo. Curso de álgebra. 3ª.ed. Rio de Janeiro: IMPA, 2002. 226 p. ISBN 852440079X
- Milies, César Polcino, Coelho, Sônia Pitta. Números: Uma introdução à Matemática. 3ª.ed. São Paulo: Editora da Universidade de São Paulo, 2003. ISBN 8531404584
- Moreira, Carlos Gustavo Tamm de Araujo, Saldanha, Nicolau C. Primos de Mersenne: e outros primos muito grandes. IMPA, 1999. 81 p. v. 1. ISBN 8524401494
- Brochero Martínez, Fabio , Moreira, Carlos Gustavo , Saldanha, Nicolau, Tengan, Eduardo. Teoria dos Números: um passeio com primos e outros números familiares pelo mundo inteiro. IMPA, 2010. 450 p. v. 1. ISBN 8524403125
- Ribenboim, Paulo. Números primos: Mistérios e records. Rio de Janeiro: IMPA, 2001. 292 p. ISBN 8524401680
- Santos, José Plínio de Oliveira. Introdução à Teoria dos Números. Rio de Janeiro: IMPA, 2007. 198 p. ISBN 9788524401428
Livros em inglês
[editar | editar código-fonte]- Apostol, Tom M.. Introduction to Analytic Number Theory. Springer, 1976. 352 p. ISBN 0387901639
- Cassels, J. W. S.. An introduction to diophantine aproximations. Cambridge University Press, 1957.
- Cohn, Harvey. A Second Course in Number Theory. New York: John Wiley & Sons, 1962. 276 p.
- Dickson, Leonard Eugene. History of the theory of numbers: Divisibility and Primality. American Mathematical Society, 1966. 486 p. ISBN 0821819348
- Gauss, Carl Friedrich. Disquisitiones Arithmeticae. Springer, 1986. 472 p. ISBN 0387962542
- Goldman, Jay R.. The Queen of Mathematics: An Historically Motivated Guide to Number Theory. A.K. Peters, 1998. 525 p. ISBN 1568810067
- Guy, Richard K.. Unsolved Problems in Number Theory. 3ª.ed. Springer, 2004. 437 p. v. 1. ISBN 0387208607
- Hardy, G. H., Wright, Edward Maitland. An Introduction to the Theory of Numbers. 5ª.ed. Oxford University Press, 1979. 456 p. ISBN 0198531710
- Honsberger, R.. A Theorem of Gabriel Lamé: Ch. 7 in Mathematical Gems II. Washington, DC: Math. Assoc. Amer., 1976. 54-57 p. ISBN 0883853027
- Ireland, Kenneth F., Rosen, Michael. A Classical Introduction to Modern Number Theory. Springer, 1990. ISBN 038797329X
- Jones, Gareth A., Jones, Josephine Mary. Elementary Number Theory. Springer, 1998. 301 p. ISBN 3540761977
- Knuth, Donald. The Art of Computer Programming: Seminumerical Algorithms. 3ª.ed. Addison-Wesley, 1997. v. 2. ISBN 0201896842
- LeVeque, William Judson. Fundamentals of Number Theory. Dover, 1996. 288 p. ISBN 0486689069
- Matiyasevich, Yuri V.. Hilbert's Tenth Problem. MIT Press, 1993. 288 p. ISBN 0262132958
- Niven, Herbert Ivan, Zuckerman, Herbert S.. Introduction to the Theory of Numbers. John Wiley & Sons, 1968. 296 p. ISBN 0471641537
- Ribenboim, Paulo. The New Book of Prime Number Records. Springer, 1996. 572 p. ISBN 0387944575
- Saidak, Filip. A New Proof of Euclid's Theorem, Amer. Math. Monthly 113, no. 10, 937--938. 2006.
- Sierpiński, Wacław. 250 Problems in Elementary Number Theory. American Elsevier Pub. Co., 1970. 125 p. ISBN 0444000712
- Stewart, Ian. Algebraic Number Theory and Fermat's Last Theorem. A K Peters, Ltd., 2002. ISBN 1568811195
- Vinogradov, Ivan Matveevich. Elements of number theory. Courier Dover Publications, 2003. 240 p. ISBN 0486495302
Outras referências
[editar | editar código-fonte]- The Elements of Euclid, por Isaac Todhunter - Disponível no Wikisource
- Jurkiewicz, Samuel. Divisibilidade e Números Inteiros: Introdução à Aritmética Modular. Apostila 1 do estágio para bolsistas da OBMEP.
- Neves, Vítor. Introdução à Teoria dos Números. Universidade de Aveiro. 2001.
- Weisstein, Eric W. Lamé's Theorem. From MathWorld - A Wolfram Web Resource.
- Viggo Brun. Euclidean algorithms and musical theory. Enseignement Mathématique, 10:125–137, 1964.
- Toussaint, Godfried. The Euclidean Algorithm Generates Traditional Musical Rhythms.
- Shoup, Victor. A Computational Introduction to Number Theory and Algebra (Version 1) - Um eBook disponibilizado sob a Creative Commons license (Attribution-NonCommercial-NoDerivs 2.0).
Neste capítulo, será discutido quão eficiente é o algoritmo de Euclides para o cálculo do MDC. De forma mais precisa, se forem dados dois números inteiros:
- Quantas etapas (divisões) do algoritmo são necessárias para que um resto seja zero?
Fazendo estimativas
[editar | editar código-fonte]Recorde-se que o algoritmo baseia-se na construção da sequência:
cujos termos verificam as seguintes igualdades:
| 1 | |||
| 2 | |||
| k-1 | |||
| k | pois |
O algoritmo fornece , que é o último resto não nulo, obtido em passos (divisões).
Uma observação importante é que o resto de uma divisão é sempre menor que a metade do dividendo:
Sendo a primeira desigualdade válida porque e a segunda porque . Deste modo, tem-se
e em geral
- , para cada .
Assim, comparando os termos cujos índices são pares, segue:
Por indução, resulta para cada termo:
De modo análogo, ao comparar os termos ímpares, e usar novamente indução, segue:
Com isso, a sequência dos decresce geometricamente, pois está fixado. O fato de ser uma sequência decrescente já havia sido demonstrado quando se justificou o funcionamento do algoritmo de Euclides. A novidade aqui é a velocidade com que a sequência decresce. Pelos cálculos anteriores, os restos diminuem, no mínimo, tão rápido quanto os termos da progressão geométrica .
A questão colocada era: Quantas divisões são necessárias para que o resto seja zero?
Analisando a progressão geométrica dada anteriormente, conclui-se que algum de seus termos é menor do que . Nesse caso, o resto correspondente será nulo, e o algoritmo para. Para ser mais exato, como
o menor índice inteiro que torna menor que é
Onde denota o maior inteiro que não supera (a parte inteira de ).
Então , e consequentemente , pois os restos são números inteiros não-negativos.
Assim, sabendo que o algoritmo para exatamente quando , conlui-se que tal índice não pode ser maior que , em símbolos:
Para melhor compreender o significado dessa estimativa, considere que tem dígitos decimais. Então:
Aplicando o logaritmo em ambos os membros da segunda desigualdade, resulta
Logo, , que para valores grandes de é aproximadamente .
Embora esta não seja a melhor aproximação para , já é bastante útil, pois mostra que o número de etapas cresce linearmente com o número de dígitos de .
O pior caso
[editar | editar código-fonte]Para obter uma estimativa mais precisa do número de etapas que o algoritmo de Euclides leva para determinar o MDC de dois números, será considerada a seguinte questão:
- Qual é o menor valor de para o qual o algoritmo leva passos?
Veja alguns exemplos utilizando a representação matricial do algoritmo:
Para :
Para :
Para :
É fácil perceber que é mínimo quando os valores forem todos iguais a , cada entrada da matriz é um polinômio nas variáveis (que são positivas), e cujos coeficiêntes são (se puder, acrescente uma justificativa mais formal).
Se cada quociente for substituído por na fórmula de recorrência
Esta passará a ser:
Que vale para satisfazendo .
A nova relação lembra a fórmula que define a sequência de Fibonacci, embora esteja "ao contrário".
| Este módulo tem a seguinte tarefa pendente: Conferir se o expoente k+1 está correto ou se deveria ser k, na próxima equação |
Matricialmente, as condições produzem as seguintes igualdades:
- , sendo que .
Com um simples uso do princípio de indução finita, consegue-se:
- , desde que .
Deste modo,
Como , segue que
- Teorema
Dado , sejam e os menores números tais que o algoritmo de Euclides aplicado a e leva exatamente passos, então e .
Exemplificando
[editar | editar código-fonte]Para determinar o valor de , seria necessário efetuar cinco divisões:
Logo, . Aproveitando este exemplo, observe que:
No entanto, se qualquer dos números for menor, o algoritmo requer menos etapas. Por exemplo, ao determinar tem-se:
Donde, .
Já o cálculo de é ainda mais simples:
Portanto, .
Melhorando as estimativas
[editar | editar código-fonte]Sabendo qual é o pior caso para a aplicação do algoritmo de Euclides, pode-se deduzir uma melhor estimativa de sua eficiência. Uma análise mais elaborada que aquela apresentada no início do capítulo fornece o seguinte resultado:
Teorema de Lamé
[editar | editar código-fonte]- Teorema
O número de passos (de divisões) no algoritmo de Euclides com entradas e é limitado superiormente por vezes a quantidade de dígitos decimais em .
Gabriel-Lamé
 |
| Este módulo tem a seguinte tarefa pendente: Incluir breve biografia sobre Lamé. |
Para demonstrar o teorema de Lamé, é importante ter em mente algumas propriedades relacionadas a sequência de Fibonacci e ao número de ouro:
Tem-se:
| Demonstração |
|---|
| A verificação é direta, exigindo cálculos bastante simples. |
- , arredondado para o inteiro mais próximo.
| Demonstração |
|---|
| Utilizando a fórmula de Binet, basta observar que o módulo de é menor que , e consequentemente, quando , tem-se |
| Demonstração |
|---|
A justificativa será dada por indução:
|
| Demonstração |
|---|
| De fato, valem as seguintes equivalências:
Mas (verifique a partir de ), e pois Sendo que esta última desigualdade é verdadeira. |
Como foi visto anteriormente, quando é exige exatamente passos, é tem-se e . Logo,
Aplicando o logaritmo em ambos os menbros, segue:
ou seja
Mas , então:
- , onde é o número de dígitos de
Demonstração da fórmula de Binet
[editar | editar código-fonte]Nesta seção, será deduzida a fórmula de Binet:
onde e .
A principal razão para se utilizar está fórmula, em vez da definição recursiva da sequência de Fibonacci, é que ela permite a obtenção de um termo da sequência sem precisar calcular os anteriores.
| Demonstração |
|---|
| A relação entre os termos da sequência pode ser descrita matricialmente da seguinte forma:
Para simplificar, será adotada a seguinte notação: A partir de um simples argumento de indução (veja exercício 1), obtem-se: Neste ponto, recorre-se à Álgebra linear, para obter um jeito simples de calcular o produto acima. Se puder ser escrito
A partir daí será bastante simples conseguir a fórmula explicita para (a segunda componente do vetor à esquerda), pois seriam constantes. É, portanto, necessário determinar essas constantes, a começar pelos auto-valores de . Tem-se: Logo , ou seja, Assim, (que implica ) ou . O primeiro caso não é de interesse, pois auto-vetores não são nulos. Note que a equação acima possui duas raízes: Além disso, se é raiz da equação, então para cada , o vetor
Em particular, se , os auto-vetores correspondentes a cada raiz da equação quadrática são: De modo que e Resta escrever conforme se pretendia. Isso é fácil, já que são conhecidos e : Da segunda equação, segue que . Substituindo esse valor na primeira equação, resulta: Como (verifique!), tem-se . Logo, . Assim, . Em consequência: Em particular, escrevendo a igualdade entre as segundas coordenadas desses vetores, obtem-se a fórmula desejada: |
Exercícios
[editar | editar código-fonte]- Verifique, utilizando o princípio de indução, que:
- Escreva outra demonstração para a fórmula de Binet, utilizando o princípio de indução.
Por enquanto, não há muitos exercícios sobre este capítulo. O leitor está convidado a adicionar mais ítens a essa seção, para ajudar a melhorar o texto.
Neste capítulo serão estudados certos problemas cuja solução envolve conceitos da teoria de números que foram tratados nos capítulos anteriores.
Considere o seguinte problema:
Se existem notas de 2 e de 5 reais, quais são os valores que podem ser obtidos combinando algumas dessas notas?
Matematicamente, o que se quer saber é:
Quais os valores de para os quais a solução possui alguma solução inteira?
Em geral, as equações que surgem no contexto da teoria de números devem ser resolvidas no conjunto dos números inteiros. Este tipo de equação é conhecido como equação diofantina.
As equações diofantinas lineares
[editar | editar código-fonte]A equação que surgiu do exemplo apresentado no início do capítulo é apenas um caso particular da seguinte: Aqui, os inteiros e são fixados.
Quando é que tal equação possui solução?
O próximo teorema responde exatamente essa pergunta.
- Teorema
Dados existem tais que se, e somente se, Além disso, se é solução, então todas as soluções são da forma: e onde e
| Demonstração |
|---|
| Primeiramente, observe que se é uma solução, então (pela linearidade da divisibilidade).
Reciprocamente, se então Mas pelo teorema de Bézout, existem inteiros tais que Logo, multiplicando cada membro por tem-se: ou seja, basta tomar e e será uma solução.
Se for uma solução conhecida, qualquer outra solução satizfaz: Então ou seja, Tomando é possível escrever Donde: Claramente e Logo ou seja, existe tal que Portanto, Usando essa expressão em resulta Disto se conclui que |
Assim como acontece em problemas que envolvem equações diferenciais, para determinar o conjunto solução de uma equação diofantina, encontra-se primeiramente uma solução particular, e combina-se a mesma com a solução da equação homogênea (no caso, )
Agora é possível resolver o problema proposto no início.
Aplicação
[editar | editar código-fonte]Será que existem números inteiros que verificam
Conforme o teorema indica, para que exista uma solução (e portanto infinitas) é preciso que
Pelo algoritmo de Euclides obtem-se além de Multiplicando ambos os membros por segue que:
Assim, as demais soluções são da forma:
No contexto em que o problema foi colocado, é exigido que as soluções não sejam números negativos. Disto seguem as seguintes restrições:
que são equivalentes a
Para que exista algum valor inteiro nesse intervalo, é suficiente que ou seja,
Note que a condição anterior é suficiente, mas não necessária, pois para alguns valores de também há soluções:
A conclusão final é que, utilizando apenas notas de e de é possível obter qualquer valor inteiro maior que ou igual a
Interpretação geométrica
[editar | editar código-fonte]Sabe-se que o conjunto dos pontos (com coordenadas reais) que verificam a equação é representado por uma reta sobre o plano cartesiano. Então as soluções da equação diofantina são representadas pelos pontos da reta que possuem ambas as coordenadas inteiras.
Diferença de quadrados
[editar | editar código-fonte]Um outro problema que pode ser tratado com as ferramentas desenvolvidas até agora é a busca de soluções inteiras para a seguinte equação:
Buscar tais soluções significa determinar se existe algum inteiro que pode ser escrito como soma de dois quadrados perfeitos. Se a resposta for afirmativa, será interessante saber exatamente quais são os números inteiros que são soma de quadrados.
Estes são alguns exemplos desse tipo de problema:
- tem soluções inteiras?
- tem soluções inteiras?
Para poder entender a estratégia para a resolução desse tipo de problema, considere que a segunda equação tenha alguma solução
O que se pode afirmar sobre esses dois números inteiros?
Primeiramente, deve valer ou seja, a soma e a diferença das soluções devem ser divisores de Sabe-se, por exemplo, que Será que existem inteiros tais que
Por inspeção, percebe-se que e servem, logo
E quanto ao outro problema?
É possível encontrar um par de divisores de (por exemplo, e ) tais que um seja a soma, e outro a diferença das soluções?
Observe:
Divisores de
Você é capaz de encontrar alguma linha dessa tabela contendo a soma e a diferença de dois números inteiros? Justifique.
Em vez de continuar tratando o problema baseando-se em exemplos particulares, considere que existem satisfazeno a equação em sua forma geral:
Conforme anteriormente, conclui-se que, para alguma escolha de tais que tem-se e ou seja, para tais divisores de existe uma solução para o sistema:
Equivalentemente, tais inteiros são também solução do sistema:
Se você interpretar essas equações adequadamente, concluirá que devem ter a mesma paridade (ser ambos pares ou ambos ímpares). De fato, se um deles for par e o outro for ímpar, sua soma será um número ímpar, e consequentemente não poderá ser escrita como para nenhum valor inteiro
Na verdade, com pouca ou nenhuma argumentação extra, prova-se a validade do seguinte teorema
Teorema
[editar | editar código-fonte]- Teorema
Um número inteiro pode ser escrito como a diferença de dois quadrados perfeitos, se e somente se é ímpar ou múltiplo de
| Demonstração |
|---|
| A argumentação precedente mostrou que se então sendo que têm a mesma paridade.
Reciprocamente, se têm a mesma paridade, então sua soma e sua diferença são números pares, significando que o sistema possui uma solução. Mas o conjunto solução deste sistema coincide com o de: Logo, Para finalizar a demonstração, note que as paridades de são iguais se, e somente se:
Mas são ímpares se, e somente se, é ímpar. Além disso, para que sejam pares, é necessário e suficiente que e Neste caso, ou seja, é múltiplo de |
Uma forma direta de obter a representação de como diferença de quadrados é a seguinte:
- Se é múltiplo de
- Nessa situação,
- Se é ímpar.
- Nesse caso,
Exemplo
[editar | editar código-fonte]Com esse resultado, conclúi-se que não há solução para o problema dado em um exemplo anterior:
De fato, não é ímpar e nem múltiplo de
Por outro lado, usando a fórmula anterior, fica fácil resolver:
Como segue que
Ternos pitagóricos
[editar | editar código-fonte]Um pouco de história
 Pitágoras foi um matemático e filósofo grego nascido por volta de 570 a.C., na ilha de Samos. Ele é creditado pela demonstração de uma importante relação entre os lados de um triangulo retângulo, hoje conhecida como o teorema de Pitágoras, cujo enunciado é geralmente resumido da seguinte forma: |
Um terno pitagórico é uma tripla de números inteiros que satisfazem a equação:
Por exemplo, então é um terno pitagórico. Obviamente, também é um terno pitagórico, mas este último caso é trivial e sem interesse, portanto não será considerado na discussão que segue. O objetivo dessa seção é determinar em que circunstâncias a equação tem solução não trivial (não todos nulos).
É possível simplificar a investigação, considerando somento o caso em que são primos entre si. De fato, se então:
Na verdade, se for uma solução, então o máximo divisor comum destes números verifica as seguintes igualdades:
| Justificativa |
|---|
| Fica a cargo do leitor justificar este fato. Sinta-se livre para melhorar a qualidade deste texto, incluindo a justificativa na versão online deste material. |
Em particular, não pode haver não podem ser ambos pares.
Por outro lado, os inteiros também não podem ser ambos ímpares.
- De fato, se assim ocorresse, valeria:
- para algum inteiro
- para algum inteiro
- Deste modo, elevando cada um destes números ao quadrado, resultaria:
- e
- Donde:
- Ou seja, a soma dos quadrados de e seria par, mas não pertenceria a
- No entanto, sempre que é par, tem-se par e consequentemente
- Logo, quando são ambos ímpares, a soma de seus quadrados não pode ser um quadrado perfeito.
Segue que dos inteiros um é ímpar e outro é par. Sem perda de generalidade, pode-se supor que é par e é ímpar.
Uma outra forma de escrever a equação original é:
A partir daí, pode-se deduzir outras informações sobre os inteiros que a satisfazem. Por exemplo, pois:
A segunda implicação vale pois Logo,
Mas não pode ocorrer senão:
e como é par, também seria, coisa que não é possível já que
Assim, o quadrado perfeito é o produto de dois números primos entre si. Disso decorre que cada um deles deve ser um quadrado perfeito (veja o exercício 1), ou seja:
que equivale a:
Portanto, quando três números inteiros primos entre si (e não todos nulos) satizfazem a equação:
devem existir inteiros ímpares e primos entre si, tais que e:
Claramente, para quaisquer inteiros os valores de obtidos pelas fórmulas acima são ternos pitagóricos, pois:
Exemplos
[editar | editar código-fonte]Pode-se obter facilmente uma dezena de ternos pitagóricos utilizando as fórmulas:
Alguns deles são listados na tabela a seguir:
parâmetros ternos pitagóricos 3 1 3 4 5 5 1 5 12 13 7 1 7 24 25 9 1 9 40 41 5 3 15 8 17 7 3 21 20 29
Note ainda que toda solução é da forma:
onde:
Observações
[editar | editar código-fonte]A fórmula clássica para a obtenção de ternos pitagóricos é conhecida como Fórmula de Euclides, por ter sido apresentada nos Elementos de Euclides é a seguinte:
Tal fórmula é equivalente àquela deduzida anteriormente, como se pode verificar facilmente:
| Demonstração |
|---|
| De fato, foi mostrado que se com então não têm a mesma paridade. Adimitindo que seja ímpar e que seja par, conclui-se que é impar e portanto:
Mas é verdade que pois a soma e a diferença de dois números ímpares são números pares. Donde que é equivalente a: sendo que Disso se conclui também que: |
Exercícios
[editar | editar código-fonte]- Mostre que se com primos entre si, então são quadrados perfeitos.
Carl Friedrich Gauss
 Carl Friedrich Gauss foi um famoso matemático, astrônomo e físico alemão. |
| Este módulo tem a seguinte tarefa pendente: Incluir breve biografia sobre Carl Friedrich Gauss, enfatizando suas contribuições na teoria de números. |
Definição
[editar | editar código-fonte]- Definição
O inteiro é dito congruente ao inteiro módulo , quando . Neste caso, escreve-se .
Com essa notação, tem-se para quaisquer inteiros :
pois
e
Como se pode ver na próxima tabela, onde são listadas todas as combinações possíveis para e módulo , a soma de dois quadrados nunca é congruente a módulo .
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 2 |
Em outras palavras, o simples cálculo feito acima mostra que ao somar dois quadrados perfeitos, o sucessor do resultado nunca é múltiplo de .
- Nota
Sendo assim, a notação para congruências, introduzida por Gauss evita o uso de várias constantes () que não são relevantes durante grande parte dos cálculos envolvendo divisibilidade. Atente para a semelhança (visual) entre as seguintes expressões:
- Observação
Conforme o algoritmo da divisão, dados e existem únicos de modo que:
- , com
Isso significa que qualquer inteiro é congruente ao seu resto na divisão por um inteiro não nulo . Uma vez que o resto obtido é único, pode-se definir para cada inteiro fixado, uma função que a cada número associa o resto da divisão de por . A imagem de por esta função é denotada por . Mais precisamente:
Quando não houver risco de confusão, o índice será omitido e será escrito apenas em vez de .
A congruência vista como uma relação de equivalência
[editar | editar código-fonte]A partir da noção de congruência módulo um certo inteiro , pode-se definir uma relação sobre o conjunto dos números inteiros da seguinte forma:
Como será mostrado logo a diante, a relação assim definida satisfaz as propriedades de reflexividade, simetria, transitividade. Sendo, por isso, considerada uma relação de equivalência:
De modo geral, é sempre possível construir uma relação de equivalência sobre um conjunto a partir de uma função cujo domínio seja . De fato, se for definido que:
então será uma relação de equivalência em , pois :
E destas propriedades da igualdade seguem as propriedades correspondentes para a relação . Em particular, tomando , e , conclui-se que a congruência é uma relação de equivalência.
Compatibilidade com as operações
[editar | editar código-fonte]Um fato importante, que não pode deixar de ser mencionado é que a relação de congruência é compatível com as operações do anel dos números inteiros, a saber, a adição e a multiplicação. Uma operação é compatível com uma relação de equivalência quando a partir de
pode-se concluir que
No caso da relação de congruência, vê-se que a mesma é compatível tanto com a adição quanto com a multiplicação de números inteiros, como é sintetizado no próximo resultado.
- Teorema
Se são números inteiros tais que:
A verificação deste resultado é bem simples, como se pode ver a seguir.
| Demonstração |
|---|
| Primeiramente, da hipótese sobre os inteiros , segue que existem inteiros , tais que
Donde,
ou seja,
Além disso, onde Logo, ou seja, |
O anel das classes de congruência
[editar | editar código-fonte]
Sempre que se tem uma relação de equivalência sobre um conjunto é possível definir uma partição de tal conjunto. Uma coleção de subconjuntos de é chamada de partição de se todo elemento de pertence a exatamente um elemento de . Os elementos de são disjuntos dois a dois, e sua união é o próprio conjunto .
Para definir uma partição de , usando a congruência módulo , primeiramente define-se para cada inteiro a classe de equivalência de , segundo , como:
Quando o inteiro estiver subentendido, será utilizado apenas para denotar .
Nesses termos, o quociente de pela relação é a partição dada por:
Por simplicidade, denota-se simplesmente como .
Uma das formas de visualizar essa partição de é imaginar que sobre um barbante foram marcados todos os números inteiros, separando os números adjacentes sempre por uma mesma distância. Depois disso, para obter uma representação de , enrola-se o barbante em torno de uma circunferência (infinitas vezes!), de modo que o zero ocupe a mesma posição que os inteiros . Você pode então pensar nos elementos de como sendo os n pontos sobre a circunferência que se formou. Veja uma ilustração:
Deste modo, cada ponto da circunferência representa uma das classes de equivalência módulo , ou seja, o conjunto dos números inteiros que ficaram sobrepostos naquele ponto da circunferência.
Mas o que há de interessante em particionar o conjunto dos números inteiros?
A grande utilidade de separar os números inteiros em várias classes de congruência é consequência da compatibilidade da congruência com as operações de adição e multiplicação: Sabendo-se que elas são compatíveis, é possível definir em cada novas operações de adição e multiplicação. O procedimento é o seguinte:
Fixado um inteiro , e dadas as classes , define-se:
- (ou simplesmente )
Em outras palavras, a soma (produto) das classes de congruência dos inteiros é a classe de congruência de sua soma (produto).
É importante notar onde é utilizada a compatibilidade da congruência com as operações de : Dadas duas classes de equivalência e , tanto faz obter como sendo ou . Todas essas classes são idênticas!
Mais do que isso, ao definir essas operações, torna-se um anel com unidade, ou seja, são válidas as seguintes propriedades:
Além disso, tem-se um homomorfismo de anéis entre e :
- Recordando...
- Um anel com unidade é um conjunto R equipado com duas operações binárias + : R × R ? R e · : R × R ? R (onde × denota o produto cartesiano), chamadas de adição e multiplicação, tais que:
- (R, +) é um grupo abeliano com elemento identidade, isto é, para todo a, b, c em R, vale o seguinte:
- (a + b) + c = a + (b + c) (+ é associativa)
- 0 + a = a (0 é a identidade)
- a + b = b + a (+ é comutativa)
- para cada a em R existe −a em R tal que a + (−a) = (−a) + a = 0 (−a é o elemento inverso de a)
- (R, ·) é um monóide com elemento identidade 1, isto é, para todo a, b, c em R, vale:
- (a · b) · c = a · (b · c) (· é associativa)
- 1 · a = a · 1 = a (1 é a identidade)
- Multiplicação se distribui em relação a adição:
- a · (b + c) = (a · b) + (a · c)
- (a + b) · c = (a · c) + (b · c).
- (R, +) é um grupo abeliano com elemento identidade, isto é, para todo a, b, c em R, vale o seguinte:
Exemplos
[editar | editar código-fonte]As próximas tabelas são as tabuadas das operações de adição e multiplicação no anel . Note que este é um número composto, e que (por esse motivo) existem elementos não nulos em cujo produto é zero (no caso, ).
0 1 2 3 4 5 0 0 1 2 3 4 5 1 1 2 3 4 5 0 2 2 3 4 5 0 1 3 3 4 5 0 1 2 4 4 5 0 1 2 3 5 5 0 1 2 3 4
0 1 2 3 4 5 0 0 0 0 0 0 0 1 0 1 2 3 4 5 2 0 2 4 0 2 4 3 0 3 0 3 0 3 4 0 4 2 0 4 2 5 0 5 4 3 2 1
Outro fato curioso que pode ser identificado em alguns anéis é a presença de elementos nilpotentes, ou seja, tais que alguma de suas potências é nula. Por exemplo, em , tem-se .
Veja a tábua de multiplicação completa para o anel de inteiros módulo :
0 1 2 3 4 5 6 7 8 9 10 11 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 2 3 4 5 6 7 8 9 10 11 2 0 2 4 6 8 10 0 2 4 6 8 10 3 0 3 6 9 0 3 6 9 0 3 6 9 4 0 4 8 0 4 8 0 4 8 0 4 8 5 0 5 10 3 8 1 6 11 4 9 2 7 6 0 6 0 6 0 6 0 6 0 6 0 6 7 0 7 2 9 4 11 6 1 8 3 10 5 8 0 8 4 0 8 4 0 8 4 0 8 4 9 0 9 6 3 0 9 6 3 0 9 6 3 10 0 10 8 6 4 2 0 10 8 6 4 2 11 0 11 10 9 8 7 6 5 4 3 2 1
O próximo passo é tentar compreender algebricamente os conjuntos .
| Este módulo tem a seguinte tarefa pendente: Revisar/reescrever/excluir o trecho a seguir (até onde diz "Corolário da p7"). |
No próximo diagrama pode ser observada a estrutura aditiva de :
é subgrupo aditivo de .
, subgrupo aditivo de
- . Logo
Menor tal que .
- gera , ou seja são os blocos básicos.
Observe a seguinte tabela, onde constam as ordens aditivas módulo 6.
1 2 3 4 5 6 0 0 1 1 2 3 4 5 0 2 2 4 0 3 3 0 4 4 2 0 5 5 4 3 2 1 0
- . Logo
Corolário da p7
- Se p é primo então não tem subgrupos triviais.
- ou . Isso implica que ou , donde é domínio de integridade e portanto, é corpo (todo domínio finito é corpo).
Exemplo:
0 1 2 3 4 0 0 0 0 0 0 1 0 1 2 3 4 2 0 2 4 1 3 3 0 3 1 4 2 4 0 4 3 2 1
Outra consequencia é que, fixado z não nulo em Z_p, a função , definida por é injetiva, pois se , ou seja, , então . Como , pode-se concluir que , ou seja, .
Em particular, da sobrejetividade de , e de (a imagem de ), segue a existência de tal que , ou seja, tal que .
Algebricamente, o significado da sobrejetividade de é a existência de um elemento inverso para cada (quando p é primo). No entanto, a argumentação anterior é não construtiva, pois não indica um método para obter o inverso de um certo .
Pode-se obter outra justificativa para a existência de elementos inversos em usando o teorema de Bezout. De fato, se, e somente se, , ou seja, se, e somente, . Usando o algoritmo de Euclides, pode-se então encontrar tais que . Em particular, usando congruências módulo p segue . Donde , ou seja, . Portanto, o procurado é simplesmente .
Resumindo
[editar | editar código-fonte]Os fatos mais relevantes apresentados na discussão feita até agora podem ser sintetizados da seguinte forma:
- Para qualquer , tem-se um anel finito ;
- São equivalentes:
- é corpo;
- é um domínio;
- é um número primo;
- (propriedades algébricas dos conjuntos -- anéis regulares --correspondem a propriedades aritméticas dos numeros inteiros ).
- São também equivalentes:
- tem divisores de zero;
- é um número composto;
Unidades
[editar | editar código-fonte]Para um inteiro arbitrário (seja ele primo ou não), podem ser considerada a questão:
- Quais elementos de são inversíveis?
Antes de responder essa pergunta, convém introduzir uma notação específica para denotar o conjunto dos elementos que possuem inverso multiplicativo:
- Definição
Um elemento de é chamado de unidade quando possui inverso multiplicativo. O conjunto das unidades de denota-se por .
Exemplos
[editar | editar código-fonte]- Se p é número primo, então
Propriedades das unidades
[editar | editar código-fonte]Pode-se verificar que para qualquer , o conjunto , das unidades de , é um grupo multiplicativo finito. Em particular, sempre que , tem-se . Além disso, e existe tal que .
Novamente, a estrutura de reflete as propriedades aritméticas de . Para melhor entender o que isso significa, é interessante saber para cada a quantidade de elementos de . É razoável esperar que esse número varie com , então o melhor é definir uma função que associa com a cardinalidade de :
- Definição
A função de Euler é a função que associa a cada o número de elementos de :
- Observações
- Convenciona-se que .
- O valor é justamente a quantidade de números de a que são coprimos com :
| Demonstração |
|---|
| De fato, se , então existe tal que , ou seja, . Isso significa que , ou seja, que . Segue que .
Reciprocamente, se , então (teorema de Bézout). Logo, e consequentemente, . Neste caso, . |
Exemplos
[editar | editar código-fonte]- Quando é um número primo, tem-se .
- Por outro lado, para números compostos, pode ser bem menor do que . Em particular, .
Curiosidades
[editar | editar código-fonte]O valor de é justamente a quantidade de frações próprias não negativas com denominador (ou seja, ) que já estão na forma irredutível.
Exemplo
[editar | editar código-fonte]No caso apresentado anteriormente, temos as seguintes frações próprias com tal denominador:
Escrevendo cada uma delas na forma irredutível obtém-se:
Pode-se então conferir que, como era esperado, só duas das frações já estavam em sua forma irredutível: e .
Note que ao escrever cada fração em sua forma irredutível os denominadores que surgem são todos divisores de . Além disso, tem-se:
- 1 fração com denominador 1
- 1 fração com denominador 2
- 2 fração com denominador 3
- 2 fração com denominador 6
Totalizando frações. Por outro lado, a seguinte tabela indica um fato muito interessante:
d Número de frações com denominador d 1 1 1 2 1 1 3 2 2 6 2 2
Percebe-se que as duas últimas colunas coincidem. Mas o que isso significa?
Isso quer dizer que o número é, na verdade, igual a soma dos valores de cada um dos divisores . Em símbolos:
Pode-se verificar que essas duas propriedades são válidas em geral:
- é igual à quantidade de frações próprias não negativas com denominador que estão na forma irredutível.
| Justificativa |
|---|
| Fica a cargo do leitor justificar este fato. Sinta-se livre para melhorar a qualidade deste texto, incluindo a justificativa na versão online deste material. |
Equações lineares
[editar | editar código-fonte]Uma questão muito natural é investigar em que casos há alguma solução para equações lineares do tipo
Exemplo de equação linear com apenas uma solução
[editar | editar código-fonte]Considere em a seguinte equação:
ou, em termos de congruências,
Sabendo que , é possível determinar tais que
Por exemplo, pode-se tomar e . Outra possibilidade é e . Neste caso, nota-se que:
ou seja,
significando que em , ou seja, que neste anel o inverso multiplicativo de é ele mesmo. Sabendo disso, é possível resolver
de forma análoga à utilizada em : Multiplicando-se ambos os membros pelo inverso de , segue:
ou seja,
Conclui-se então que, nesse exemplo, há uma somente uma solução em para a equação dada. Observe ainda que o número não teve qualquer influência no número de soluções para o problema. Isso pode ser percebido considerando para cada o resultado de sua multiplicação por :
0 1 2 3 4 5 6 7 0 3 6 1 4 7 2 5
Note que se tem uma permutação dos elementos de e que, portanto, o único elemento que é levado em ao ser multiplicado por é o . Essa unicidade permaneceria se o fosse trocado por qualquer outro elemento.
Exemplo de equação linear sem solução
[editar | editar código-fonte]Considere a seguinte equação em :
que em termos de congruências se escreve como
Já foi mostrado que ela é equivalente à seguinte equação em :
ou seja,
É claro que tal equação não admite sequer uma solução inteira, uma vez que à esquerda tem-se um número par e a direita um ímpar, ou para ser mais exato, pois .
Exemplo de equação linear com duas soluções
[editar | editar código-fonte]Como um último exemplo antes de conhecer o teorema que dá uma resposta definitiva sobre o número de soluções de uma equação linear em , considere em a equação:
ou seja,
O problema de encontrar soluções para esta equação é equivalente a encontrar inteiros tais que:
Dividindo ambos os membros por dois, obtem-se
ou seja,
Em termos de congruências, segue:
Os números inteiros que verificam essa congruência são os termos da progressão aritmética:
No entanto, como as soluções são buscadas em , devemos considerar os números acima módulo :
ou seja, o conjunto das soluções é:
Em suma, verificou-se através dos exemplos anteriores que é possível encontrar em equações do tipo que possuam uma ou duas soluções, e mesmo equações que não adimitem solução. Essa é uma notavel diferença entre corpos (como , e ) e anéis. Por exemplo, em ou você deve estar habituado a resolver , simplesmente dividindo os dois membros por (e talvez descrevendo esse procedimento como "passar o para o lado direito, dividindo..."). No entanto, é tempo de notar que isso só é possível quando possui inverso. Em , todo número não nulo possui inverso. Mas isso não é verdade em todo anel! Por essa razão torna-se necessário tomar algum cuidado ao resolver equações nos aneis . Fique atento!
Exercícios
[editar | editar código-fonte]- Mostre que, se e é um polinômio com coeficientes inteiros, então .
- Que propriedade aritmética do número inteiro corresponde a existência de elementos nilpotentes em ? (Lembre-se, um elemento é nilpotente quando alguma de suas potências inteiras é igual a zero)
Conjectura de Goldbach
[editar | editar código-fonte]Dos problemas matemáticos em aberto, a conjectura de Goldbach, embora considerada de pouca relevância por alguns, é muito importante para os estudos dos números primos. Em uma carta a Euler em 1742, Goldbach sugeriu o seguinte: todo número natural par maior que 3 pode ser escrito como soma de dois números primos.
Lista dos primeiros 10.000 números primos
[editar | editar código-fonte]A tabela a seguir foi produzida de forma automatizada, utilizando uma macro elaborada justamente para este fim. O código fonte está disponível em uma seção posterior desta página, e foi escrito na linguagem de programação OpenOffice.org Basic.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 | 53 | 59 | 61 | 67 | 71 |
| 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 | 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 |
| 179 | 181 | 191 | 193 | 197 | 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 | 367 | 373 | 379 | 383 | 389 | 397 | 401 | 409 |
| 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 | 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 |
| 547 | 557 | 563 | 569 | 571 | 577 | 587 | 593 | 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 | 769 | 773 | 787 | 797 | 809 |
| 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 | 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 |
| 947 | 953 | 967 | 971 | 977 | 983 | 991 | 997 | 1009 | 1013 | 1019 | 1021 | 1031 | 1033 | 1039 | 1049 | 1051 | 1061 | 1063 | 1069 |
| 1087 | 1091 | 1093 | 1097 | 1103 | 1109 | 1117 | 1123 | 1129 | 1151 | 1153 | 1163 | 1171 | 1181 | 1187 | 1193 | 1201 | 1213 | 1217 | 1223 |
| 1229 | 1231 | 1237 | 1249 | 1259 | 1277 | 1279 | 1283 | 1289 | 1291 | 1297 | 1301 | 1303 | 1307 | 1319 | 1321 | 1327 | 1361 | 1367 | 1373 |
| 1381 | 1399 | 1409 | 1423 | 1427 | 1429 | 1433 | 1439 | 1447 | 1451 | 1453 | 1459 | 1471 | 1481 | 1483 | 1487 | 1489 | 1493 | 1499 | 1511 |
| 1523 | 1531 | 1543 | 1549 | 1553 | 1559 | 1567 | 1571 | 1579 | 1583 | 1597 | 1601 | 1607 | 1609 | 1613 | 1619 | 1621 | 1627 | 1637 | 1657 |
| 1663 | 1667 | 1669 | 1693 | 1697 | 1699 | 1709 | 1721 | 1723 | 1733 | 1741 | 1747 | 1753 | 1759 | 1777 | 1783 | 1787 | 1789 | 1801 | 1811 |
| 1823 | 1831 | 1847 | 1861 | 1867 | 1871 | 1873 | 1877 | 1879 | 1889 | 1901 | 1907 | 1913 | 1931 | 1933 | 1949 | 1951 | 1973 | 1979 | 1987 |
| 1993 | 1997 | 1999 | 2003 | 2011 | 2017 | 2027 | 2029 | 2039 | 2053 | 2063 | 2069 | 2081 | 2083 | 2087 | 2089 | 2099 | 2111 | 2113 | 2129 |
| 2131 | 2137 | 2141 | 2143 | 2153 | 2161 | 2179 | 2203 | 2207 | 2213 | 2221 | 2237 | 2239 | 2243 | 2251 | 2267 | 2269 | 2273 | 2281 | 2287 |
| 2293 | 2297 | 2309 | 2311 | 2333 | 2339 | 2341 | 2347 | 2351 | 2357 | 2371 | 2377 | 2381 | 2383 | 2389 | 2393 | 2399 | 2411 | 2417 | 2423 |
| 2437 | 2441 | 2447 | 2459 | 2467 | 2473 | 2477 | 2503 | 2521 | 2531 | 2539 | 2543 | 2549 | 2551 | 2557 | 2579 | 2591 | 2593 | 2609 | 2617 |
| 2621 | 2633 | 2647 | 2657 | 2659 | 2663 | 2671 | 2677 | 2683 | 2687 | 2689 | 2693 | 2699 | 2707 | 2711 | 2713 | 2719 | 2729 | 2731 | 2741 |
| 2749 | 2753 | 2767 | 2777 | 2789 | 2791 | 2797 | 2801 | 2803 | 2819 | 2833 | 2837 | 2843 | 2851 | 2857 | 2861 | 2879 | 2887 | 2897 | 2903 |
| 2909 | 2917 | 2927 | 2939 | 2953 | 2957 | 2963 | 2969 | 2971 | 2999 | 3001 | 3011 | 3019 | 3023 | 3037 | 3041 | 3049 | 3061 | 3067 | 3079 |
| 3083 | 3089 | 3109 | 3119 | 3121 | 3137 | 3163 | 3167 | 3169 | 3181 | 3187 | 3191 | 3203 | 3209 | 3217 | 3221 | 3229 | 3251 | 3253 | 3257 |
| 3259 | 3271 | 3299 | 3301 | 3307 | 3313 | 3319 | 3323 | 3329 | 3331 | 3343 | 3347 | 3359 | 3361 | 3371 | 3373 | 3389 | 3391 | 3407 | 3413 |
| 3433 | 3449 | 3457 | 3461 | 3463 | 3467 | 3469 | 3491 | 3499 | 3511 | 3517 | 3527 | 3529 | 3533 | 3539 | 3541 | 3547 | 3557 | 3559 | 3571 |
| 3581 | 3583 | 3593 | 3607 | 3613 | 3617 | 3623 | 3631 | 3637 | 3643 | 3659 | 3671 | 3673 | 3677 | 3691 | 3697 | 3701 | 3709 | 3719 | 3727 |
| 3733 | 3739 | 3761 | 3767 | 3769 | 3779 | 3793 | 3797 | 3803 | 3821 | 3823 | 3833 | 3847 | 3851 | 3853 | 3863 | 3877 | 3881 | 3889 | 3907 |
| 3911 | 3917 | 3919 | 3923 | 3929 | 3931 | 3943 | 3947 | 3967 | 3989 | 4001 | 4003 | 4007 | 4013 | 4019 | 4021 | 4027 | 4049 | 4051 | 4057 |
| 4073 | 4079 | 4091 | 4093 | 4099 | 4111 | 4127 | 4129 | 4133 | 4139 | 4153 | 4157 | 4159 | 4177 | 4201 | 4211 | 4217 | 4219 | 4229 | 4231 |
| 4241 | 4243 | 4253 | 4259 | 4261 | 4271 | 4273 | 4283 | 4289 | 4297 | 4327 | 4337 | 4339 | 4349 | 4357 | 4363 | 4373 | 4391 | 4397 | 4409 |
| 4421 | 4423 | 4441 | 4447 | 4451 | 4457 | 4463 | 4481 | 4483 | 4493 | 4507 | 4513 | 4517 | 4519 | 4523 | 4547 | 4549 | 4561 | 4567 | 4583 |
| 4591 | 4597 | 4603 | 4621 | 4637 | 4639 | 4643 | 4649 | 4651 | 4657 | 4663 | 4673 | 4679 | 4691 | 4703 | 4721 | 4723 | 4729 | 4733 | 4751 |
| 4759 | 4783 | 4787 | 4789 | 4793 | 4799 | 4801 | 4813 | 4817 | 4831 | 4861 | 4871 | 4877 | 4889 | 4903 | 4909 | 4919 | 4931 | 4933 | 4937 |
| 4943 | 4951 | 4957 | 4967 | 4969 | 4973 | 4987 | 4993 | 4999 | 5003 | 5009 | 5011 | 5021 | 5023 | 5039 | 5051 | 5059 | 5077 | 5081 | 5087 |
| 5099 | 5101 | 5107 | 5113 | 5119 | 5147 | 5153 | 5167 | 5171 | 5179 | 5189 | 5197 | 5209 | 5227 | 5231 | 5233 | 5237 | 5261 | 5273 | 5279 |
| 5281 | 5297 | 5303 | 5309 | 5323 | 5333 | 5347 | 5351 | 5381 | 5387 | 5393 | 5399 | 5407 | 5413 | 5417 | 5419 | 5431 | 5437 | 5441 | 5443 |
| 5449 | 5471 | 5477 | 5479 | 5483 | 5501 | 5503 | 5507 | 5519 | 5521 | 5527 | 5531 | 5557 | 5563 | 5569 | 5573 | 5581 | 5591 | 5623 | 5639 |
| 5641 | 5647 | 5651 | 5653 | 5657 | 5659 | 5669 | 5683 | 5689 | 5693 | 5701 | 5711 | 5717 | 5737 | 5741 | 5743 | 5749 | 5779 | 5783 | 5791 |
| 5801 | 5807 | 5813 | 5821 | 5827 | 5839 | 5843 | 5849 | 5851 | 5857 | 5861 | 5867 | 5869 | 5879 | 5881 | 5897 | 5903 | 5923 | 5927 | 5939 |
| 5953 | 5981 | 5987 | 6007 | 6011 | 6029 | 6037 | 6043 | 6047 | 6053 | 6067 | 6073 | 6079 | 6089 | 6091 | 6101 | 6113 | 6121 | 6131 | 6133 |
| 6143 | 6151 | 6163 | 6173 | 6197 | 6199 | 6203 | 6211 | 6217 | 6221 | 6229 | 6247 | 6257 | 6263 | 6269 | 6271 | 6277 | 6287 | 6299 | 6301 |
| 6311 | 6317 | 6323 | 6329 | 6337 | 6343 | 6353 | 6359 | 6361 | 6367 | 6373 | 6379 | 6389 | 6397 | 6421 | 6427 | 6449 | 6451 | 6469 | 6473 |
| 6481 | 6491 | 6521 | 6529 | 6547 | 6551 | 6553 | 6563 | 6569 | 6571 | 6577 | 6581 | 6599 | 6607 | 6619 | 6637 | 6653 | 6659 | 6661 | 6673 |
| 6679 | 6689 | 6691 | 6701 | 6703 | 6709 | 6719 | 6733 | 6737 | 6761 | 6763 | 6779 | 6781 | 6791 | 6793 | 6803 | 6823 | 6827 | 6829 | 6833 |
| 6841 | 6857 | 6863 | 6869 | 6871 | 6883 | 6899 | 6907 | 6911 | 6917 | 6947 | 6949 | 6959 | 6961 | 6967 | 6971 | 6977 | 6983 | 6991 | 6997 |
| 7001 | 7013 | 7019 | 7027 | 7039 | 7043 | 7057 | 7069 | 7079 | 7103 | 7109 | 7121 | 7127 | 7129 | 7151 | 7159 | 7177 | 7187 | 7193 | 7207 |
| 7211 | 7213 | 7219 | 7229 | 7237 | 7243 | 7247 | 7253 | 7283 | 7297 | 7307 | 7309 | 7321 | 7331 | 7333 | 7349 | 7351 | 7369 | 7393 | 7411 |
| 7417 | 7433 | 7451 | 7457 | 7459 | 7477 | 7481 | 7487 | 7489 | 7499 | 7507 | 7517 | 7523 | 7529 | 7537 | 7541 | 7547 | 7549 | 7559 | 7561 |
| 7573 | 7577 | 7583 | 7589 | 7591 | 7603 | 7607 | 7621 | 7639 | 7643 | 7649 | 7669 | 7673 | 7681 | 7687 | 7691 | 7699 | 7703 | 7717 | 7723 |
| 7727 | 7741 | 7753 | 7757 | 7759 | 7789 | 7793 | 7817 | 7823 | 7829 | 7841 | 7853 | 7867 | 7873 | 7877 | 7879 | 7883 | 7901 | 7907 | 7919 |
| 7927 | 7933 | 7937 | 7949 | 7951 | 7963 | 7993 | 8009 | 8011 | 8017 | 8039 | 8053 | 8059 | 8069 | 8081 | 8087 | 8089 | 8093 | 8101 | 8111 |
| 8117 | 8123 | 8147 | 8161 | 8167 | 8171 | 8179 | 8191 | 8209 | 8219 | 8221 | 8231 | 8233 | 8237 | 8243 | 8263 | 8269 | 8273 | 8287 | 8291 |
| 8293 | 8297 | 8311 | 8317 | 8329 | 8353 | 8363 | 8369 | 8377 | 8387 | 8389 | 8419 | 8423 | 8429 | 8431 | 8443 | 8447 | 8461 | 8467 | 8501 |
| 8513 | 8521 | 8527 | 8537 | 8539 | 8543 | 8563 | 8573 | 8581 | 8597 | 8599 | 8609 | 8623 | 8627 | 8629 | 8641 | 8647 | 8663 | 8669 | 8677 |
| 8681 | 8689 | 8693 | 8699 | 8707 | 8713 | 8719 | 8731 | 8737 | 8741 | 8747 | 8753 | 8761 | 8779 | 8783 | 8803 | 8807 | 8819 | 8821 | 8831 |
| 8837 | 8839 | 8849 | 8861 | 8863 | 8867 | 8887 | 8893 | 8923 | 8929 | 8933 | 8941 | 8951 | 8963 | 8969 | 8971 | 8999 | 9001 | 9007 | 9011 |
| 9013 | 9029 | 9041 | 9043 | 9049 | 9059 | 9067 | 9091 | 9103 | 9109 | 9127 | 9133 | 9137 | 9151 | 9157 | 9161 | 9173 | 9181 | 9187 | 9199 |
| 9203 | 9209 | 9221 | 9227 | 9239 | 9241 | 9257 | 9277 | 9281 | 9283 | 9293 | 9311 | 9319 | 9323 | 9337 | 9341 | 9343 | 9349 | 9371 | 9377 |
| 9391 | 9397 | 9403 | 9413 | 9419 | 9421 | 9431 | 9433 | 9437 | 9439 | 9461 | 9463 | 9467 | 9473 | 9479 | 9491 | 9497 | 9511 | 9521 | 9533 |
| 9539 | 9547 | 9551 | 9587 | 9601 | 9613 | 9619 | 9623 | 9629 | 9631 | 9643 | 9649 | 9661 | 9677 | 9679 | 9689 | 9697 | 9719 | 9721 | 9733 |
| 9739 | 9743 | 9749 | 9767 | 9769 | 9781 | 9787 | 9791 | 9803 | 9811 | 9817 | 9829 | 9833 | 9839 | 9851 | 9857 | 9859 | 9871 | 9883 | 9887 |
| 9901 | 9907 | 9923 | 9929 | 9931 | 9941 | 9949 | 9967 | 9973 | 10007 | 10009 | 10037 | 10039 | 10061 | 10067 | 10069 | 10079 | 10091 | 10093 | 10099 |
| 10103 | 10111 | 10133 | 10139 | 10141 | 10151 | 10159 | 10163 | 10169 | 10177 | 10181 | 10193 | 10211 | 10223 | 10243 | 10247 | 10253 | 10259 | 10267 | 10271 |
| 10273 | 10289 | 10301 | 10303 | 10313 | 10321 | 10331 | 10333 | 10337 | 10343 | 10357 | 10369 | 10391 | 10399 | 10427 | 10429 | 10433 | 10453 | 10457 | 10459 |
| 10463 | 10477 | 10487 | 10499 | 10501 | 10513 | 10529 | 10531 | 10559 | 10567 | 10589 | 10597 | 10601 | 10607 | 10613 | 10627 | 10631 | 10639 | 10651 | 10657 |
| 10663 | 10667 | 10687 | 10691 | 10709 | 10711 | 10723 | 10729 | 10733 | 10739 | 10753 | 10771 | 10781 | 10789 | 10799 | 10831 | 10837 | 10847 | 10853 | 10859 |
| 10861 | 10867 | 10883 | 10889 | 10891 | 10903 | 10909 | 10937 | 10939 | 10949 | 10957 | 10973 | 10979 | 10987 | 10993 | 11003 | 11027 | 11047 | 11057 | 11059 |
| 11069 | 11071 | 11083 | 11087 | 11093 | 11113 | 11117 | 11119 | 11131 | 11149 | 11159 | 11161 | 11171 | 11173 | 11177 | 11197 | 11213 | 11239 | 11243 | 11251 |
| 11257 | 11261 | 11273 | 11279 | 11287 | 11299 | 11311 | 11317 | 11321 | 11329 | 11351 | 11353 | 11369 | 11383 | 11393 | 11399 | 11411 | 11423 | 11437 | 11443 |
| 11447 | 11467 | 11471 | 11483 | 11489 | 11491 | 11497 | 11503 | 11519 | 11527 | 11549 | 11551 | 11579 | 11587 | 11593 | 11597 | 11617 | 11621 | 11633 | 11657 |
| 11677 | 11681 | 11689 | 11699 | 11701 | 11717 | 11719 | 11731 | 11743 | 11777 | 11779 | 11783 | 11789 | 11801 | 11807 | 11813 | 11821 | 11827 | 11831 | 11833 |
| 11839 | 11863 | 11867 | 11887 | 11897 | 11903 | 11909 | 11923 | 11927 | 11933 | 11939 | 11941 | 11953 | 11959 | 11969 | 11971 | 11981 | 11987 | 12007 | 12011 |
| 12037 | 12041 | 12043 | 12049 | 12071 | 12073 | 12097 | 12101 | 12107 | 12109 | 12113 | 12119 | 12143 | 12149 | 12157 | 12161 | 12163 | 12197 | 12203 | 12211 |
| 12227 | 12239 | 12241 | 12251 | 12253 | 12263 | 12269 | 12277 | 12281 | 12289 | 12301 | 12323 | 12329 | 12343 | 12347 | 12373 | 12377 | 12379 | 12391 | 12401 |
| 12409 | 12413 | 12421 | 12433 | 12437 | 12451 | 12457 | 12473 | 12479 | 12487 | 12491 | 12497 | 12503 | 12511 | 12517 | 12527 | 12539 | 12541 | 12547 | 12553 |
| 12569 | 12577 | 12583 | 12589 | 12601 | 12611 | 12613 | 12619 | 12637 | 12641 | 12647 | 12653 | 12659 | 12671 | 12689 | 12697 | 12703 | 12713 | 12721 | 12739 |
| 12743 | 12757 | 12763 | 12781 | 12791 | 12799 | 12809 | 12821 | 12823 | 12829 | 12841 | 12853 | 12889 | 12893 | 12899 | 12907 | 12911 | 12917 | 12919 | 12923 |
| 12941 | 12953 | 12959 | 12967 | 12973 | 12979 | 12983 | 13001 | 13003 | 13007 | 13009 | 13033 | 13037 | 13043 | 13049 | 13063 | 13093 | 13099 | 13103 | 13109 |
| 13121 | 13127 | 13147 | 13151 | 13159 | 13163 | 13171 | 13177 | 13183 | 13187 | 13217 | 13219 | 13229 | 13241 | 13249 | 13259 | 13267 | 13291 | 13297 | 13309 |
| 13313 | 13327 | 13331 | 13337 | 13339 | 13367 | 13381 | 13397 | 13399 | 13411 | 13417 | 13421 | 13441 | 13451 | 13457 | 13463 | 13469 | 13477 | 13487 | 13499 |
| 13513 | 13523 | 13537 | 13553 | 13567 | 13577 | 13591 | 13597 | 13613 | 13619 | 13627 | 13633 | 13649 | 13669 | 13679 | 13681 | 13687 | 13691 | 13693 | 13697 |
| 13709 | 13711 | 13721 | 13723 | 13729 | 13751 | 13757 | 13759 | 13763 | 13781 | 13789 | 13799 | 13807 | 13829 | 13831 | 13841 | 13859 | 13873 | 13877 | 13879 |
| 13883 | 13901 | 13903 | 13907 | 13913 | 13921 | 13931 | 13933 | 13963 | 13967 | 13997 | 13999 | 14009 | 14011 | 14029 | 14033 | 14051 | 14057 | 14071 | 14081 |
| 14083 | 14087 | 14107 | 14143 | 14149 | 14153 | 14159 | 14173 | 14177 | 14197 | 14207 | 14221 | 14243 | 14249 | 14251 | 14281 | 14293 | 14303 | 14321 | 14323 |
| 14327 | 14341 | 14347 | 14369 | 14387 | 14389 | 14401 | 14407 | 14411 | 14419 | 14423 | 14431 | 14437 | 14447 | 14449 | 14461 | 14479 | 14489 | 14503 | 14519 |
| 14533 | 14537 | 14543 | 14549 | 14551 | 14557 | 14561 | 14563 | 14591 | 14593 | 14621 | 14627 | 14629 | 14633 | 14639 | 14653 | 14657 | 14669 | 14683 | 14699 |
| 14713 | 14717 | 14723 | 14731 | 14737 | 14741 | 14747 | 14753 | 14759 | 14767 | 14771 | 14779 | 14783 | 14797 | 14813 | 14821 | 14827 | 14831 | 14843 | 14851 |
| 14867 | 14869 | 14879 | 14887 | 14891 | 14897 | 14923 | 14929 | 14939 | 14947 | 14951 | 14957 | 14969 | 14983 | 15013 | 15017 | 15031 | 15053 | 15061 | 15073 |
| 15077 | 15083 | 15091 | 15101 | 15107 | 15121 | 15131 | 15137 | 15139 | 15149 | 15161 | 15173 | 15187 | 15193 | 15199 | 15217 | 15227 | 15233 | 15241 | 15259 |
| 15263 | 15269 | 15271 | 15277 | 15287 | 15289 | 15299 | 15307 | 15313 | 15319 | 15329 | 15331 | 15349 | 15359 | 15361 | 15373 | 15377 | 15383 | 15391 | 15401 |
| 15413 | 15427 | 15439 | 15443 | 15451 | 15461 | 15467 | 15473 | 15493 | 15497 | 15511 | 15527 | 15541 | 15551 | 15559 | 15569 | 15581 | 15583 | 15601 | 15607 |
| 15619 | 15629 | 15641 | 15643 | 15647 | 15649 | 15661 | 15667 | 15671 | 15679 | 15683 | 15727 | 15731 | 15733 | 15737 | 15739 | 15749 | 15761 | 15767 | 15773 |
| 15787 | 15791 | 15797 | 15803 | 15809 | 15817 | 15823 | 15859 | 15877 | 15881 | 15887 | 15889 | 15901 | 15907 | 15913 | 15919 | 15923 | 15937 | 15959 | 15971 |
| 15973 | 15991 | 16001 | 16007 | 16033 | 16057 | 16061 | 16063 | 16067 | 16069 | 16073 | 16087 | 16091 | 16097 | 16103 | 16111 | 16127 | 16139 | 16141 | 16183 |
| 16187 | 16189 | 16193 | 16217 | 16223 | 16229 | 16231 | 16249 | 16253 | 16267 | 16273 | 16301 | 16319 | 16333 | 16339 | 16349 | 16361 | 16363 | 16369 | 16381 |
| 16411 | 16417 | 16421 | 16427 | 16433 | 16447 | 16451 | 16453 | 16477 | 16481 | 16487 | 16493 | 16519 | 16529 | 16547 | 16553 | 16561 | 16567 | 16573 | 16603 |
| 16607 | 16619 | 16631 | 16633 | 16649 | 16651 | 16657 | 16661 | 16673 | 16691 | 16693 | 16699 | 16703 | 16729 | 16741 | 16747 | 16759 | 16763 | 16787 | 16811 |
| 16823 | 16829 | 16831 | 16843 | 16871 | 16879 | 16883 | 16889 | 16901 | 16903 | 16921 | 16927 | 16931 | 16937 | 16943 | 16963 | 16979 | 16981 | 16987 | 16993 |
| 17011 | 17021 | 17027 | 17029 | 17033 | 17041 | 17047 | 17053 | 17077 | 17093 | 17099 | 17107 | 17117 | 17123 | 17137 | 17159 | 17167 | 17183 | 17189 | 17191 |
| 17203 | 17207 | 17209 | 17231 | 17239 | 17257 | 17291 | 17293 | 17299 | 17317 | 17321 | 17327 | 17333 | 17341 | 17351 | 17359 | 17377 | 17383 | 17387 | 17389 |
| 17393 | 17401 | 17417 | 17419 | 17431 | 17443 | 17449 | 17467 | 17471 | 17477 | 17483 | 17489 | 17491 | 17497 | 17509 | 17519 | 17539 | 17551 | 17569 | 17573 |
| 17579 | 17581 | 17597 | 17599 | 17609 | 17623 | 17627 | 17657 | 17659 | 17669 | 17681 | 17683 | 17707 | 17713 | 17729 | 17737 | 17747 | 17749 | 17761 | 17783 |
| 17789 | 17791 | 17807 | 17827 | 17837 | 17839 | 17851 | 17863 | 17881 | 17891 | 17903 | 17909 | 17911 | 17921 | 17923 | 17929 | 17939 | 17957 | 17959 | 17971 |
| 17977 | 17981 | 17987 | 17989 | 18013 | 18041 | 18043 | 18047 | 18049 | 18059 | 18061 | 18077 | 18089 | 18097 | 18119 | 18121 | 18127 | 18131 | 18133 | 18143 |
| 18149 | 18169 | 18181 | 18191 | 18199 | 18211 | 18217 | 18223 | 18229 | 18233 | 18251 | 18253 | 18257 | 18269 | 18287 | 18289 | 18301 | 18307 | 18311 | 18313 |
| 18329 | 18341 | 18353 | 18367 | 18371 | 18379 | 18397 | 18401 | 18413 | 18427 | 18433 | 18439 | 18443 | 18451 | 18457 | 18461 | 18481 | 18493 | 18503 | 18517 |
| 18521 | 18523 | 18539 | 18541 | 18553 | 18583 | 18587 | 18593 | 18617 | 18637 | 18661 | 18671 | 18679 | 18691 | 18701 | 18713 | 18719 | 18731 | 18743 | 18749 |
| 18757 | 18773 | 18787 | 18793 | 18797 | 18803 | 18839 | 18859 | 18869 | 18899 | 18911 | 18913 | 18917 | 18919 | 18947 | 18959 | 18973 | 18979 | 19001 | 19009 |
| 19013 | 19031 | 19037 | 19051 | 19069 | 19073 | 19079 | 19081 | 19087 | 19121 | 19139 | 19141 | 19157 | 19163 | 19181 | 19183 | 19207 | 19211 | 19213 | 19219 |
| 19231 | 19237 | 19249 | 19259 | 19267 | 19273 | 19289 | 19301 | 19309 | 19319 | 19333 | 19373 | 19379 | 19381 | 19387 | 19391 | 19403 | 19417 | 19421 | 19423 |
| 19427 | 19429 | 19433 | 19441 | 19447 | 19457 | 19463 | 19469 | 19471 | 19477 | 19483 | 19489 | 19501 | 19507 | 19531 | 19541 | 19543 | 19553 | 19559 | 19571 |
| 19577 | 19583 | 19597 | 19603 | 19609 | 19661 | 19681 | 19687 | 19697 | 19699 | 19709 | 19717 | 19727 | 19739 | 19751 | 19753 | 19759 | 19763 | 19777 | 19793 |
| 19801 | 19813 | 19819 | 19841 | 19843 | 19853 | 19861 | 19867 | 19889 | 19891 | 19913 | 19919 | 19927 | 19937 | 19949 | 19961 | 19963 | 19973 | 19979 | 19991 |
| 19993 | 19997 | 20011 | 20021 | 20023 | 20029 | 20047 | 20051 | 20063 | 20071 | 20089 | 20101 | 20107 | 20113 | 20117 | 20123 | 20129 | 20143 | 20147 | 20149 |
| 20161 | 20173 | 20177 | 20183 | 20201 | 20219 | 20231 | 20233 | 20249 | 20261 | 20269 | 20287 | 20297 | 20323 | 20327 | 20333 | 20341 | 20347 | 20353 | 20357 |
| 20359 | 20369 | 20389 | 20393 | 20399 | 20407 | 20411 | 20431 | 20441 | 20443 | 20477 | 20479 | 20483 | 20507 | 20509 | 20521 | 20533 | 20543 | 20549 | 20551 |
| 20563 | 20593 | 20599 | 20611 | 20627 | 20639 | 20641 | 20663 | 20681 | 20693 | 20707 | 20717 | 20719 | 20731 | 20743 | 20747 | 20749 | 20753 | 20759 | 20771 |
| 20773 | 20789 | 20807 | 20809 | 20849 | 20857 | 20873 | 20879 | 20887 | 20897 | 20899 | 20903 | 20921 | 20929 | 20939 | 20947 | 20959 | 20963 | 20981 | 20983 |
| 21001 | 21011 | 21013 | 21017 | 21019 | 21023 | 21031 | 21059 | 21061 | 21067 | 21089 | 21101 | 21107 | 21121 | 21139 | 21143 | 21149 | 21157 | 21163 | 21169 |
| 21179 | 21187 | 21191 | 21193 | 21211 | 21221 | 21227 | 21247 | 21269 | 21277 | 21283 | 21313 | 21317 | 21319 | 21323 | 21341 | 21347 | 21377 | 21379 | 21383 |
| 21391 | 21397 | 21401 | 21407 | 21419 | 21433 | 21467 | 21481 | 21487 | 21491 | 21493 | 21499 | 21503 | 21517 | 21521 | 21523 | 21529 | 21557 | 21559 | 21563 |
| 21569 | 21577 | 21587 | 21589 | 21599 | 21601 | 21611 | 21613 | 21617 | 21647 | 21649 | 21661 | 21673 | 21683 | 21701 | 21713 | 21727 | 21737 | 21739 | 21751 |
| 21757 | 21767 | 21773 | 21787 | 21799 | 21803 | 21817 | 21821 | 21839 | 21841 | 21851 | 21859 | 21863 | 21871 | 21881 | 21893 | 21911 | 21929 | 21937 | 21943 |
| 21961 | 21977 | 21991 | 21997 | 22003 | 22013 | 22027 | 22031 | 22037 | 22039 | 22051 | 22063 | 22067 | 22073 | 22079 | 22091 | 22093 | 22109 | 22111 | 22123 |
| 22129 | 22133 | 22147 | 22153 | 22157 | 22159 | 22171 | 22189 | 22193 | 22229 | 22247 | 22259 | 22271 | 22273 | 22277 | 22279 | 22283 | 22291 | 22303 | 22307 |
| 22343 | 22349 | 22367 | 22369 | 22381 | 22391 | 22397 | 22409 | 22433 | 22441 | 22447 | 22453 | 22469 | 22481 | 22483 | 22501 | 22511 | 22531 | 22541 | 22543 |
| 22549 | 22567 | 22571 | 22573 | 22613 | 22619 | 22621 | 22637 | 22639 | 22643 | 22651 | 22669 | 22679 | 22691 | 22697 | 22699 | 22709 | 22717 | 22721 | 22727 |
| 22739 | 22741 | 22751 | 22769 | 22777 | 22783 | 22787 | 22807 | 22811 | 22817 | 22853 | 22859 | 22861 | 22871 | 22877 | 22901 | 22907 | 22921 | 22937 | 22943 |
| 22961 | 22963 | 22973 | 22993 | 23003 | 23011 | 23017 | 23021 | 23027 | 23029 | 23039 | 23041 | 23053 | 23057 | 23059 | 23063 | 23071 | 23081 | 23087 | 23099 |
| 23117 | 23131 | 23143 | 23159 | 23167 | 23173 | 23189 | 23197 | 23201 | 23203 | 23209 | 23227 | 23251 | 23269 | 23279 | 23291 | 23293 | 23297 | 23311 | 23321 |
| 23327 | 23333 | 23339 | 23357 | 23369 | 23371 | 23399 | 23417 | 23431 | 23447 | 23459 | 23473 | 23497 | 23509 | 23531 | 23537 | 23539 | 23549 | 23557 | 23561 |
| 23563 | 23567 | 23581 | 23593 | 23599 | 23603 | 23609 | 23623 | 23627 | 23629 | 23633 | 23663 | 23669 | 23671 | 23677 | 23687 | 23689 | 23719 | 23741 | 23743 |
| 23747 | 23753 | 23761 | 23767 | 23773 | 23789 | 23801 | 23813 | 23819 | 23827 | 23831 | 23833 | 23857 | 23869 | 23873 | 23879 | 23887 | 23893 | 23899 | 23909 |
| 23911 | 23917 | 23929 | 23957 | 23971 | 23977 | 23981 | 23993 | 24001 | 24007 | 24019 | 24023 | 24029 | 24043 | 24049 | 24061 | 24071 | 24077 | 24083 | 24091 |
| 24097 | 24103 | 24107 | 24109 | 24113 | 24121 | 24133 | 24137 | 24151 | 24169 | 24179 | 24181 | 24197 | 24203 | 24223 | 24229 | 24239 | 24247 | 24251 | 24281 |
| 24317 | 24329 | 24337 | 24359 | 24371 | 24373 | 24379 | 24391 | 24407 | 24413 | 24419 | 24421 | 24439 | 24443 | 24469 | 24473 | 24481 | 24499 | 24509 | 24517 |
| 24527 | 24533 | 24547 | 24551 | 24571 | 24593 | 24611 | 24623 | 24631 | 24659 | 24671 | 24677 | 24683 | 24691 | 24697 | 24709 | 24733 | 24749 | 24763 | 24767 |
| 24781 | 24793 | 24799 | 24809 | 24821 | 24841 | 24847 | 24851 | 24859 | 24877 | 24889 | 24907 | 24917 | 24919 | 24923 | 24943 | 24953 | 24967 | 24971 | 24977 |
| 24979 | 24989 | 25013 | 25031 | 25033 | 25037 | 25057 | 25073 | 25087 | 25097 | 25111 | 25117 | 25121 | 25127 | 25147 | 25153 | 25163 | 25169 | 25171 | 25183 |
| 25189 | 25219 | 25229 | 25237 | 25243 | 25247 | 25253 | 25261 | 25301 | 25303 | 25307 | 25309 | 25321 | 25339 | 25343 | 25349 | 25357 | 25367 | 25373 | 25391 |
| 25409 | 25411 | 25423 | 25439 | 25447 | 25453 | 25457 | 25463 | 25469 | 25471 | 25523 | 25537 | 25541 | 25561 | 25577 | 25579 | 25583 | 25589 | 25601 | 25603 |
| 25609 | 25621 | 25633 | 25639 | 25643 | 25657 | 25667 | 25673 | 25679 | 25693 | 25703 | 25717 | 25733 | 25741 | 25747 | 25759 | 25763 | 25771 | 25793 | 25799 |
| 25801 | 25819 | 25841 | 25847 | 25849 | 25867 | 25873 | 25889 | 25903 | 25913 | 25919 | 25931 | 25933 | 25939 | 25943 | 25951 | 25969 | 25981 | 25997 | 25999 |
| 26003 | 26017 | 26021 | 26029 | 26041 | 26053 | 26083 | 26099 | 26107 | 26111 | 26113 | 26119 | 26141 | 26153 | 26161 | 26171 | 26177 | 26183 | 26189 | 26203 |
| 26209 | 26227 | 26237 | 26249 | 26251 | 26261 | 26263 | 26267 | 26293 | 26297 | 26309 | 26317 | 26321 | 26339 | 26347 | 26357 | 26371 | 26387 | 26393 | 26399 |
| 26407 | 26417 | 26423 | 26431 | 26437 | 26449 | 26459 | 26479 | 26489 | 26497 | 26501 | 26513 | 26539 | 26557 | 26561 | 26573 | 26591 | 26597 | 26627 | 26633 |
| 26641 | 26647 | 26669 | 26681 | 26683 | 26687 | 26693 | 26699 | 26701 | 26711 | 26713 | 26717 | 26723 | 26729 | 26731 | 26737 | 26759 | 26777 | 26783 | 26801 |
| 26813 | 26821 | 26833 | 26839 | 26849 | 26861 | 26863 | 26879 | 26881 | 26891 | 26893 | 26903 | 26921 | 26927 | 26947 | 26951 | 26953 | 26959 | 26981 | 26987 |
| 26993 | 27011 | 27017 | 27031 | 27043 | 27059 | 27061 | 27067 | 27073 | 27077 | 27091 | 27103 | 27107 | 27109 | 27127 | 27143 | 27179 | 27191 | 27197 | 27211 |
| 27239 | 27241 | 27253 | 27259 | 27271 | 27277 | 27281 | 27283 | 27299 | 27329 | 27337 | 27361 | 27367 | 27397 | 27407 | 27409 | 27427 | 27431 | 27437 | 27449 |
| 27457 | 27479 | 27481 | 27487 | 27509 | 27527 | 27529 | 27539 | 27541 | 27551 | 27581 | 27583 | 27611 | 27617 | 27631 | 27647 | 27653 | 27673 | 27689 | 27691 |
| 27697 | 27701 | 27733 | 27737 | 27739 | 27743 | 27749 | 27751 | 27763 | 27767 | 27773 | 27779 | 27791 | 27793 | 27799 | 27803 | 27809 | 27817 | 27823 | 27827 |
| 27847 | 27851 | 27883 | 27893 | 27901 | 27917 | 27919 | 27941 | 27943 | 27947 | 27953 | 27961 | 27967 | 27983 | 27997 | 28001 | 28019 | 28027 | 28031 | 28051 |
| 28057 | 28069 | 28081 | 28087 | 28097 | 28099 | 28109 | 28111 | 28123 | 28151 | 28163 | 28181 | 28183 | 28201 | 28211 | 28219 | 28229 | 28277 | 28279 | 28283 |
| 28289 | 28297 | 28307 | 28309 | 28319 | 28349 | 28351 | 28387 | 28393 | 28403 | 28409 | 28411 | 28429 | 28433 | 28439 | 28447 | 28463 | 28477 | 28493 | 28499 |
| 28513 | 28517 | 28537 | 28541 | 28547 | 28549 | 28559 | 28571 | 28573 | 28579 | 28591 | 28597 | 28603 | 28607 | 28619 | 28621 | 28627 | 28631 | 28643 | 28649 |
| 28657 | 28661 | 28663 | 28669 | 28687 | 28697 | 28703 | 28711 | 28723 | 28729 | 28751 | 28753 | 28759 | 28771 | 28789 | 28793 | 28807 | 28813 | 28817 | 28837 |
| 28843 | 28859 | 28867 | 28871 | 28879 | 28901 | 28909 | 28921 | 28927 | 28933 | 28949 | 28961 | 28979 | 29009 | 29017 | 29021 | 29023 | 29027 | 29033 | 29059 |
| 29063 | 29077 | 29101 | 29123 | 29129 | 29131 | 29137 | 29147 | 29153 | 29167 | 29173 | 29179 | 29191 | 29201 | 29207 | 29209 | 29221 | 29231 | 29243 | 29251 |
| 29269 | 29287 | 29297 | 29303 | 29311 | 29327 | 29333 | 29339 | 29347 | 29363 | 29383 | 29387 | 29389 | 29399 | 29401 | 29411 | 29423 | 29429 | 29437 | 29443 |
| 29453 | 29473 | 29483 | 29501 | 29527 | 29531 | 29537 | 29567 | 29569 | 29573 | 29581 | 29587 | 29599 | 29611 | 29629 | 29633 | 29641 | 29663 | 29669 | 29671 |
| 29683 | 29717 | 29723 | 29741 | 29753 | 29759 | 29761 | 29789 | 29803 | 29819 | 29833 | 29837 | 29851 | 29863 | 29867 | 29873 | 29879 | 29881 | 29917 | 29921 |
| 29927 | 29947 | 29959 | 29983 | 29989 | 30011 | 30013 | 30029 | 30047 | 30059 | 30071 | 30089 | 30091 | 30097 | 30103 | 30109 | 30113 | 30119 | 30133 | 30137 |
| 30139 | 30161 | 30169 | 30181 | 30187 | 30197 | 30203 | 30211 | 30223 | 30241 | 30253 | 30259 | 30269 | 30271 | 30293 | 30307 | 30313 | 30319 | 30323 | 30341 |
| 30347 | 30367 | 30389 | 30391 | 30403 | 30427 | 30431 | 30449 | 30467 | 30469 | 30491 | 30493 | 30497 | 30509 | 30517 | 30529 | 30539 | 30553 | 30557 | 30559 |
| 30577 | 30593 | 30631 | 30637 | 30643 | 30649 | 30661 | 30671 | 30677 | 30689 | 30697 | 30703 | 30707 | 30713 | 30727 | 30757 | 30763 | 30773 | 30781 | 30803 |
| 30809 | 30817 | 30829 | 30839 | 30841 | 30851 | 30853 | 30859 | 30869 | 30871 | 30881 | 30893 | 30911 | 30931 | 30937 | 30941 | 30949 | 30971 | 30977 | 30983 |
| 31013 | 31019 | 31033 | 31039 | 31051 | 31063 | 31069 | 31079 | 31081 | 31091 | 31121 | 31123 | 31139 | 31147 | 31151 | 31153 | 31159 | 31177 | 31181 | 31183 |
| 31189 | 31193 | 31219 | 31223 | 31231 | 31237 | 31247 | 31249 | 31253 | 31259 | 31267 | 31271 | 31277 | 31307 | 31319 | 31321 | 31327 | 31333 | 31337 | 31357 |
| 31379 | 31387 | 31391 | 31393 | 31397 | 31469 | 31477 | 31481 | 31489 | 31511 | 31513 | 31517 | 31531 | 31541 | 31543 | 31547 | 31567 | 31573 | 31583 | 31601 |
| 31607 | 31627 | 31643 | 31649 | 31657 | 31663 | 31667 | 31687 | 31699 | 31721 | 31723 | 31727 | 31729 | 31741 | 31751 | 31769 | 31771 | 31793 | 31799 | 31817 |
| 31847 | 31849 | 31859 | 31873 | 31883 | 31891 | 31907 | 31957 | 31963 | 31973 | 31981 | 31991 | 32003 | 32009 | 32027 | 32029 | 32051 | 32057 | 32059 | 32063 |
| 32069 | 32077 | 32083 | 32089 | 32099 | 32117 | 32119 | 32141 | 32143 | 32159 | 32173 | 32183 | 32189 | 32191 | 32203 | 32213 | 32233 | 32237 | 32251 | 32257 |
| 32261 | 32297 | 32299 | 32303 | 32309 | 32321 | 32323 | 32327 | 32341 | 32353 | 32359 | 32363 | 32369 | 32371 | 32377 | 32381 | 32401 | 32411 | 32413 | 32423 |
| 32429 | 32441 | 32443 | 32467 | 32479 | 32491 | 32497 | 32503 | 32507 | 32531 | 32533 | 32537 | 32561 | 32563 | 32569 | 32573 | 32579 | 32587 | 32603 | 32609 |
| 32611 | 32621 | 32633 | 32647 | 32653 | 32687 | 32693 | 32707 | 32713 | 32717 | 32719 | 32749 | 32771 | 32779 | 32783 | 32789 | 32797 | 32801 | 32803 | 32831 |
| 32833 | 32839 | 32843 | 32869 | 32887 | 32909 | 32911 | 32917 | 32933 | 32939 | 32941 | 32957 | 32969 | 32971 | 32983 | 32987 | 32993 | 32999 | 33013 | 33023 |
| 33029 | 33037 | 33049 | 33053 | 33071 | 33073 | 33083 | 33091 | 33107 | 33113 | 33119 | 33149 | 33151 | 33161 | 33179 | 33181 | 33191 | 33199 | 33203 | 33211 |
| 33223 | 33247 | 33287 | 33289 | 33301 | 33311 | 33317 | 33329 | 33331 | 33343 | 33347 | 33349 | 33353 | 33359 | 33377 | 33391 | 33403 | 33409 | 33413 | 33427 |
| 33457 | 33461 | 33469 | 33479 | 33487 | 33493 | 33503 | 33521 | 33529 | 33533 | 33547 | 33563 | 33569 | 33577 | 33581 | 33587 | 33589 | 33599 | 33601 | 33613 |
| 33617 | 33619 | 33623 | 33629 | 33637 | 33641 | 33647 | 33679 | 33703 | 33713 | 33721 | 33739 | 33749 | 33751 | 33757 | 33767 | 33769 | 33773 | 33791 | 33797 |
| 33809 | 33811 | 33827 | 33829 | 33851 | 33857 | 33863 | 33871 | 33889 | 33893 | 33911 | 33923 | 33931 | 33937 | 33941 | 33961 | 33967 | 33997 | 34019 | 34031 |
| 34033 | 34039 | 34057 | 34061 | 34123 | 34127 | 34129 | 34141 | 34147 | 34157 | 34159 | 34171 | 34183 | 34211 | 34213 | 34217 | 34231 | 34253 | 34259 | 34261 |
| 34267 | 34273 | 34283 | 34297 | 34301 | 34303 | 34313 | 34319 | 34327 | 34337 | 34351 | 34361 | 34367 | 34369 | 34381 | 34403 | 34421 | 34429 | 34439 | 34457 |
| 34469 | 34471 | 34483 | 34487 | 34499 | 34501 | 34511 | 34513 | 34519 | 34537 | 34543 | 34549 | 34583 | 34589 | 34591 | 34603 | 34607 | 34613 | 34631 | 34649 |
| 34651 | 34667 | 34673 | 34679 | 34687 | 34693 | 34703 | 34721 | 34729 | 34739 | 34747 | 34757 | 34759 | 34763 | 34781 | 34807 | 34819 | 34841 | 34843 | 34847 |
| 34849 | 34871 | 34877 | 34883 | 34897 | 34913 | 34919 | 34939 | 34949 | 34961 | 34963 | 34981 | 35023 | 35027 | 35051 | 35053 | 35059 | 35069 | 35081 | 35083 |
| 35089 | 35099 | 35107 | 35111 | 35117 | 35129 | 35141 | 35149 | 35153 | 35159 | 35171 | 35201 | 35221 | 35227 | 35251 | 35257 | 35267 | 35279 | 35281 | 35291 |
| 35311 | 35317 | 35323 | 35327 | 35339 | 35353 | 35363 | 35381 | 35393 | 35401 | 35407 | 35419 | 35423 | 35437 | 35447 | 35449 | 35461 | 35491 | 35507 | 35509 |
| 35521 | 35527 | 35531 | 35533 | 35537 | 35543 | 35569 | 35573 | 35591 | 35593 | 35597 | 35603 | 35617 | 35671 | 35677 | 35729 | 35731 | 35747 | 35753 | 35759 |
| 35771 | 35797 | 35801 | 35803 | 35809 | 35831 | 35837 | 35839 | 35851 | 35863 | 35869 | 35879 | 35897 | 35899 | 35911 | 35923 | 35933 | 35951 | 35963 | 35969 |
| 35977 | 35983 | 35993 | 35999 | 36007 | 36011 | 36013 | 36017 | 36037 | 36061 | 36067 | 36073 | 36083 | 36097 | 36107 | 36109 | 36131 | 36137 | 36151 | 36161 |
| 36187 | 36191 | 36209 | 36217 | 36229 | 36241 | 36251 | 36263 | 36269 | 36277 | 36293 | 36299 | 36307 | 36313 | 36319 | 36341 | 36343 | 36353 | 36373 | 36383 |
| 36389 | 36433 | 36451 | 36457 | 36467 | 36469 | 36473 | 36479 | 36493 | 36497 | 36523 | 36527 | 36529 | 36541 | 36551 | 36559 | 36563 | 36571 | 36583 | 36587 |
| 36599 | 36607 | 36629 | 36637 | 36643 | 36653 | 36671 | 36677 | 36683 | 36691 | 36697 | 36709 | 36713 | 36721 | 36739 | 36749 | 36761 | 36767 | 36779 | 36781 |
| 36787 | 36791 | 36793 | 36809 | 36821 | 36833 | 36847 | 36857 | 36871 | 36877 | 36887 | 36899 | 36901 | 36913 | 36919 | 36923 | 36929 | 36931 | 36943 | 36947 |
| 36973 | 36979 | 36997 | 37003 | 37013 | 37019 | 37021 | 37039 | 37049 | 37057 | 37061 | 37087 | 37097 | 37117 | 37123 | 37139 | 37159 | 37171 | 37181 | 37189 |
| 37199 | 37201 | 37217 | 37223 | 37243 | 37253 | 37273 | 37277 | 37307 | 37309 | 37313 | 37321 | 37337 | 37339 | 37357 | 37361 | 37363 | 37369 | 37379 | 37397 |
| 37409 | 37423 | 37441 | 37447 | 37463 | 37483 | 37489 | 37493 | 37501 | 37507 | 37511 | 37517 | 37529 | 37537 | 37547 | 37549 | 37561 | 37567 | 37571 | 37573 |
| 37579 | 37589 | 37591 | 37607 | 37619 | 37633 | 37643 | 37649 | 37657 | 37663 | 37691 | 37693 | 37699 | 37717 | 37747 | 37781 | 37783 | 37799 | 37811 | 37813 |
| 37831 | 37847 | 37853 | 37861 | 37871 | 37879 | 37889 | 37897 | 37907 | 37951 | 37957 | 37963 | 37967 | 37987 | 37991 | 37993 | 37997 | 38011 | 38039 | 38047 |
| 38053 | 38069 | 38083 | 38113 | 38119 | 38149 | 38153 | 38167 | 38177 | 38183 | 38189 | 38197 | 38201 | 38219 | 38231 | 38237 | 38239 | 38261 | 38273 | 38281 |
| 38287 | 38299 | 38303 | 38317 | 38321 | 38327 | 38329 | 38333 | 38351 | 38371 | 38377 | 38393 | 38431 | 38447 | 38449 | 38453 | 38459 | 38461 | 38501 | 38543 |
| 38557 | 38561 | 38567 | 38569 | 38593 | 38603 | 38609 | 38611 | 38629 | 38639 | 38651 | 38653 | 38669 | 38671 | 38677 | 38693 | 38699 | 38707 | 38711 | 38713 |
| 38723 | 38729 | 38737 | 38747 | 38749 | 38767 | 38783 | 38791 | 38803 | 38821 | 38833 | 38839 | 38851 | 38861 | 38867 | 38873 | 38891 | 38903 | 38917 | 38921 |
| 38923 | 38933 | 38953 | 38959 | 38971 | 38977 | 38993 | 39019 | 39023 | 39041 | 39043 | 39047 | 39079 | 39089 | 39097 | 39103 | 39107 | 39113 | 39119 | 39133 |
| 39139 | 39157 | 39161 | 39163 | 39181 | 39191 | 39199 | 39209 | 39217 | 39227 | 39229 | 39233 | 39239 | 39241 | 39251 | 39293 | 39301 | 39313 | 39317 | 39323 |
| 39341 | 39343 | 39359 | 39367 | 39371 | 39373 | 39383 | 39397 | 39409 | 39419 | 39439 | 39443 | 39451 | 39461 | 39499 | 39503 | 39509 | 39511 | 39521 | 39541 |
| 39551 | 39563 | 39569 | 39581 | 39607 | 39619 | 39623 | 39631 | 39659 | 39667 | 39671 | 39679 | 39703 | 39709 | 39719 | 39727 | 39733 | 39749 | 39761 | 39769 |
| 39779 | 39791 | 39799 | 39821 | 39827 | 39829 | 39839 | 39841 | 39847 | 39857 | 39863 | 39869 | 39877 | 39883 | 39887 | 39901 | 39929 | 39937 | 39953 | 39971 |
| 39979 | 39983 | 39989 | 40009 | 40013 | 40031 | 40037 | 40039 | 40063 | 40087 | 40093 | 40099 | 40111 | 40123 | 40127 | 40129 | 40151 | 40153 | 40163 | 40169 |
| 40177 | 40189 | 40193 | 40213 | 40231 | 40237 | 40241 | 40253 | 40277 | 40283 | 40289 | 40343 | 40351 | 40357 | 40361 | 40387 | 40423 | 40427 | 40429 | 40433 |
| 40459 | 40471 | 40483 | 40487 | 40493 | 40499 | 40507 | 40519 | 40529 | 40531 | 40543 | 40559 | 40577 | 40583 | 40591 | 40597 | 40609 | 40627 | 40637 | 40639 |
| 40693 | 40697 | 40699 | 40709 | 40739 | 40751 | 40759 | 40763 | 40771 | 40787 | 40801 | 40813 | 40819 | 40823 | 40829 | 40841 | 40847 | 40849 | 40853 | 40867 |
| 40879 | 40883 | 40897 | 40903 | 40927 | 40933 | 40939 | 40949 | 40961 | 40973 | 40993 | 41011 | 41017 | 41023 | 41039 | 41047 | 41051 | 41057 | 41077 | 41081 |
| 41113 | 41117 | 41131 | 41141 | 41143 | 41149 | 41161 | 41177 | 41179 | 41183 | 41189 | 41201 | 41203 | 41213 | 41221 | 41227 | 41231 | 41233 | 41243 | 41257 |
| 41263 | 41269 | 41281 | 41299 | 41333 | 41341 | 41351 | 41357 | 41381 | 41387 | 41389 | 41399 | 41411 | 41413 | 41443 | 41453 | 41467 | 41479 | 41491 | 41507 |
| 41513 | 41519 | 41521 | 41539 | 41543 | 41549 | 41579 | 41593 | 41597 | 41603 | 41609 | 41611 | 41617 | 41621 | 41627 | 41641 | 41647 | 41651 | 41659 | 41669 |
| 41681 | 41687 | 41719 | 41729 | 41737 | 41759 | 41761 | 41771 | 41777 | 41801 | 41809 | 41813 | 41843 | 41849 | 41851 | 41863 | 41879 | 41887 | 41893 | 41897 |
| 41903 | 41911 | 41927 | 41941 | 41947 | 41953 | 41957 | 41959 | 41969 | 41981 | 41983 | 41999 | 42013 | 42017 | 42019 | 42023 | 42043 | 42061 | 42071 | 42073 |
| 42083 | 42089 | 42101 | 42131 | 42139 | 42157 | 42169 | 42179 | 42181 | 42187 | 42193 | 42197 | 42209 | 42221 | 42223 | 42227 | 42239 | 42257 | 42281 | 42283 |
| 42293 | 42299 | 42307 | 42323 | 42331 | 42337 | 42349 | 42359 | 42373 | 42379 | 42391 | 42397 | 42403 | 42407 | 42409 | 42433 | 42437 | 42443 | 42451 | 42457 |
| 42461 | 42463 | 42467 | 42473 | 42487 | 42491 | 42499 | 42509 | 42533 | 42557 | 42569 | 42571 | 42577 | 42589 | 42611 | 42641 | 42643 | 42649 | 42667 | 42677 |
| 42683 | 42689 | 42697 | 42701 | 42703 | 42709 | 42719 | 42727 | 42737 | 42743 | 42751 | 42767 | 42773 | 42787 | 42793 | 42797 | 42821 | 42829 | 42839 | 42841 |
| 42853 | 42859 | 42863 | 42899 | 42901 | 42923 | 42929 | 42937 | 42943 | 42953 | 42961 | 42967 | 42979 | 42989 | 43003 | 43013 | 43019 | 43037 | 43049 | 43051 |
| 43063 | 43067 | 43093 | 43103 | 43117 | 43133 | 43151 | 43159 | 43177 | 43189 | 43201 | 43207 | 43223 | 43237 | 43261 | 43271 | 43283 | 43291 | 43313 | 43319 |
| 43321 | 43331 | 43391 | 43397 | 43399 | 43403 | 43411 | 43427 | 43441 | 43451 | 43457 | 43481 | 43487 | 43499 | 43517 | 43541 | 43543 | 43573 | 43577 | 43579 |
| 43591 | 43597 | 43607 | 43609 | 43613 | 43627 | 43633 | 43649 | 43651 | 43661 | 43669 | 43691 | 43711 | 43717 | 43721 | 43753 | 43759 | 43777 | 43781 | 43783 |
| 43787 | 43789 | 43793 | 43801 | 43853 | 43867 | 43889 | 43891 | 43913 | 43933 | 43943 | 43951 | 43961 | 43963 | 43969 | 43973 | 43987 | 43991 | 43997 | 44017 |
| 44021 | 44027 | 44029 | 44041 | 44053 | 44059 | 44071 | 44087 | 44089 | 44101 | 44111 | 44119 | 44123 | 44129 | 44131 | 44159 | 44171 | 44179 | 44189 | 44201 |
| 44203 | 44207 | 44221 | 44249 | 44257 | 44263 | 44267 | 44269 | 44273 | 44279 | 44281 | 44293 | 44351 | 44357 | 44371 | 44381 | 44383 | 44389 | 44417 | 44449 |
| 44453 | 44483 | 44491 | 44497 | 44501 | 44507 | 44519 | 44531 | 44533 | 44537 | 44543 | 44549 | 44563 | 44579 | 44587 | 44617 | 44621 | 44623 | 44633 | 44641 |
| 44647 | 44651 | 44657 | 44683 | 44687 | 44699 | 44701 | 44711 | 44729 | 44741 | 44753 | 44771 | 44773 | 44777 | 44789 | 44797 | 44809 | 44819 | 44839 | 44843 |
| 44851 | 44867 | 44879 | 44887 | 44893 | 44909 | 44917 | 44927 | 44939 | 44953 | 44959 | 44963 | 44971 | 44983 | 44987 | 45007 | 45013 | 45053 | 45061 | 45077 |
| 45083 | 45119 | 45121 | 45127 | 45131 | 45137 | 45139 | 45161 | 45179 | 45181 | 45191 | 45197 | 45233 | 45247 | 45259 | 45263 | 45281 | 45289 | 45293 | 45307 |
| 45317 | 45319 | 45329 | 45337 | 45341 | 45343 | 45361 | 45377 | 45389 | 45403 | 45413 | 45427 | 45433 | 45439 | 45481 | 45491 | 45497 | 45503 | 45523 | 45533 |
| 45541 | 45553 | 45557 | 45569 | 45587 | 45589 | 45599 | 45613 | 45631 | 45641 | 45659 | 45667 | 45673 | 45677 | 45691 | 45697 | 45707 | 45737 | 45751 | 45757 |
| 45763 | 45767 | 45779 | 45817 | 45821 | 45823 | 45827 | 45833 | 45841 | 45853 | 45863 | 45869 | 45887 | 45893 | 45943 | 45949 | 45953 | 45959 | 45971 | 45979 |
| 45989 | 46021 | 46027 | 46049 | 46051 | 46061 | 46073 | 46091 | 46093 | 46099 | 46103 | 46133 | 46141 | 46147 | 46153 | 46171 | 46181 | 46183 | 46187 | 46199 |
| 46219 | 46229 | 46237 | 46261 | 46271 | 46273 | 46279 | 46301 | 46307 | 46309 | 46327 | 46337 | 46349 | 46351 | 46381 | 46399 | 46411 | 46439 | 46441 | 46447 |
| 46451 | 46457 | 46471 | 46477 | 46489 | 46499 | 46507 | 46511 | 46523 | 46549 | 46559 | 46567 | 46573 | 46589 | 46591 | 46601 | 46619 | 46633 | 46639 | 46643 |
| 46649 | 46663 | 46679 | 46681 | 46687 | 46691 | 46703 | 46723 | 46727 | 46747 | 46751 | 46757 | 46769 | 46771 | 46807 | 46811 | 46817 | 46819 | 46829 | 46831 |
| 46853 | 46861 | 46867 | 46877 | 46889 | 46901 | 46919 | 46933 | 46957 | 46993 | 46997 | 47017 | 47041 | 47051 | 47057 | 47059 | 47087 | 47093 | 47111 | 47119 |
| 47123 | 47129 | 47137 | 47143 | 47147 | 47149 | 47161 | 47189 | 47207 | 47221 | 47237 | 47251 | 47269 | 47279 | 47287 | 47293 | 47297 | 47303 | 47309 | 47317 |
| 47339 | 47351 | 47353 | 47363 | 47381 | 47387 | 47389 | 47407 | 47417 | 47419 | 47431 | 47441 | 47459 | 47491 | 47497 | 47501 | 47507 | 47513 | 47521 | 47527 |
| 47533 | 47543 | 47563 | 47569 | 47581 | 47591 | 47599 | 47609 | 47623 | 47629 | 47639 | 47653 | 47657 | 47659 | 47681 | 47699 | 47701 | 47711 | 47713 | 47717 |
| 47737 | 47741 | 47743 | 47777 | 47779 | 47791 | 47797 | 47807 | 47809 | 47819 | 47837 | 47843 | 47857 | 47869 | 47881 | 47903 | 47911 | 47917 | 47933 | 47939 |
| 47947 | 47951 | 47963 | 47969 | 47977 | 47981 | 48017 | 48023 | 48029 | 48049 | 48073 | 48079 | 48091 | 48109 | 48119 | 48121 | 48131 | 48157 | 48163 | 48179 |
| 48187 | 48193 | 48197 | 48221 | 48239 | 48247 | 48259 | 48271 | 48281 | 48299 | 48311 | 48313 | 48337 | 48341 | 48353 | 48371 | 48383 | 48397 | 48407 | 48409 |
| 48413 | 48437 | 48449 | 48463 | 48473 | 48479 | 48481 | 48487 | 48491 | 48497 | 48523 | 48527 | 48533 | 48539 | 48541 | 48563 | 48571 | 48589 | 48593 | 48611 |
| 48619 | 48623 | 48647 | 48649 | 48661 | 48673 | 48677 | 48679 | 48731 | 48733 | 48751 | 48757 | 48761 | 48767 | 48779 | 48781 | 48787 | 48799 | 48809 | 48817 |
| 48821 | 48823 | 48847 | 48857 | 48859 | 48869 | 48871 | 48883 | 48889 | 48907 | 48947 | 48953 | 48973 | 48989 | 48991 | 49003 | 49009 | 49019 | 49031 | 49033 |
| 49037 | 49043 | 49057 | 49069 | 49081 | 49103 | 49109 | 49117 | 49121 | 49123 | 49139 | 49157 | 49169 | 49171 | 49177 | 49193 | 49199 | 49201 | 49207 | 49211 |
| 49223 | 49253 | 49261 | 49277 | 49279 | 49297 | 49307 | 49331 | 49333 | 49339 | 49363 | 49367 | 49369 | 49391 | 49393 | 49409 | 49411 | 49417 | 49429 | 49433 |
| 49451 | 49459 | 49463 | 49477 | 49481 | 49499 | 49523 | 49529 | 49531 | 49537 | 49547 | 49549 | 49559 | 49597 | 49603 | 49613 | 49627 | 49633 | 49639 | 49663 |
| 49667 | 49669 | 49681 | 49697 | 49711 | 49727 | 49739 | 49741 | 49747 | 49757 | 49783 | 49787 | 49789 | 49801 | 49807 | 49811 | 49823 | 49831 | 49843 | 49853 |
| 49871 | 49877 | 49891 | 49919 | 49921 | 49927 | 49937 | 49939 | 49943 | 49957 | 49991 | 49993 | 49999 | 50021 | 50023 | 50033 | 50047 | 50051 | 50053 | 50069 |
| 50077 | 50087 | 50093 | 50101 | 50111 | 50119 | 50123 | 50129 | 50131 | 50147 | 50153 | 50159 | 50177 | 50207 | 50221 | 50227 | 50231 | 50261 | 50263 | 50273 |
| 50287 | 50291 | 50311 | 50321 | 50329 | 50333 | 50341 | 50359 | 50363 | 50377 | 50383 | 50387 | 50411 | 50417 | 50423 | 50441 | 50459 | 50461 | 50497 | 50503 |
| 50513 | 50527 | 50539 | 50543 | 50549 | 50551 | 50581 | 50587 | 50591 | 50593 | 50599 | 50627 | 50647 | 50651 | 50671 | 50683 | 50707 | 50723 | 50741 | 50753 |
| 50767 | 50773 | 50777 | 50789 | 50821 | 50833 | 50839 | 50849 | 50857 | 50867 | 50873 | 50891 | 50893 | 50909 | 50923 | 50929 | 50951 | 50957 | 50969 | 50971 |
| 50989 | 50993 | 51001 | 51031 | 51043 | 51047 | 51059 | 51061 | 51071 | 51109 | 51131 | 51133 | 51137 | 51151 | 51157 | 51169 | 51193 | 51197 | 51199 | 51203 |
| 51217 | 51229 | 51239 | 51241 | 51257 | 51263 | 51283 | 51287 | 51307 | 51329 | 51341 | 51343 | 51347 | 51349 | 51361 | 51383 | 51407 | 51413 | 51419 | 51421 |
| 51427 | 51431 | 51437 | 51439 | 51449 | 51461 | 51473 | 51479 | 51481 | 51487 | 51503 | 51511 | 51517 | 51521 | 51539 | 51551 | 51563 | 51577 | 51581 | 51593 |
| 51599 | 51607 | 51613 | 51631 | 51637 | 51647 | 51659 | 51673 | 51679 | 51683 | 51691 | 51713 | 51719 | 51721 | 51749 | 51767 | 51769 | 51787 | 51797 | 51803 |
| 51817 | 51827 | 51829 | 51839 | 51853 | 51859 | 51869 | 51871 | 51893 | 51899 | 51907 | 51913 | 51929 | 51941 | 51949 | 51971 | 51973 | 51977 | 51991 | 52009 |
| 52021 | 52027 | 52051 | 52057 | 52067 | 52069 | 52081 | 52103 | 52121 | 52127 | 52147 | 52153 | 52163 | 52177 | 52181 | 52183 | 52189 | 52201 | 52223 | 52237 |
| 52249 | 52253 | 52259 | 52267 | 52289 | 52291 | 52301 | 52313 | 52321 | 52361 | 52363 | 52369 | 52379 | 52387 | 52391 | 52433 | 52453 | 52457 | 52489 | 52501 |
| 52511 | 52517 | 52529 | 52541 | 52543 | 52553 | 52561 | 52567 | 52571 | 52579 | 52583 | 52609 | 52627 | 52631 | 52639 | 52667 | 52673 | 52691 | 52697 | 52709 |
| 52711 | 52721 | 52727 | 52733 | 52747 | 52757 | 52769 | 52783 | 52807 | 52813 | 52817 | 52837 | 52859 | 52861 | 52879 | 52883 | 52889 | 52901 | 52903 | 52919 |
| 52937 | 52951 | 52957 | 52963 | 52967 | 52973 | 52981 | 52999 | 53003 | 53017 | 53047 | 53051 | 53069 | 53077 | 53087 | 53089 | 53093 | 53101 | 53113 | 53117 |
| 53129 | 53147 | 53149 | 53161 | 53171 | 53173 | 53189 | 53197 | 53201 | 53231 | 53233 | 53239 | 53267 | 53269 | 53279 | 53281 | 53299 | 53309 | 53323 | 53327 |
| 53353 | 53359 | 53377 | 53381 | 53401 | 53407 | 53411 | 53419 | 53437 | 53441 | 53453 | 53479 | 53503 | 53507 | 53527 | 53549 | 53551 | 53569 | 53591 | 53593 |
| 53597 | 53609 | 53611 | 53617 | 53623 | 53629 | 53633 | 53639 | 53653 | 53657 | 53681 | 53693 | 53699 | 53717 | 53719 | 53731 | 53759 | 53773 | 53777 | 53783 |
| 53791 | 53813 | 53819 | 53831 | 53849 | 53857 | 53861 | 53881 | 53887 | 53891 | 53897 | 53899 | 53917 | 53923 | 53927 | 53939 | 53951 | 53959 | 53987 | 53993 |
| 54001 | 54011 | 54013 | 54037 | 54049 | 54059 | 54083 | 54091 | 54101 | 54121 | 54133 | 54139 | 54151 | 54163 | 54167 | 54181 | 54193 | 54217 | 54251 | 54269 |
| 54277 | 54287 | 54293 | 54311 | 54319 | 54323 | 54331 | 54347 | 54361 | 54367 | 54371 | 54377 | 54401 | 54403 | 54409 | 54413 | 54419 | 54421 | 54437 | 54443 |
| 54449 | 54469 | 54493 | 54497 | 54499 | 54503 | 54517 | 54521 | 54539 | 54541 | 54547 | 54559 | 54563 | 54577 | 54581 | 54583 | 54601 | 54617 | 54623 | 54629 |
| 54631 | 54647 | 54667 | 54673 | 54679 | 54709 | 54713 | 54721 | 54727 | 54751 | 54767 | 54773 | 54779 | 54787 | 54799 | 54829 | 54833 | 54851 | 54869 | 54877 |
| 54881 | 54907 | 54917 | 54919 | 54941 | 54949 | 54959 | 54973 | 54979 | 54983 | 55001 | 55009 | 55021 | 55049 | 55051 | 55057 | 55061 | 55073 | 55079 | 55103 |
| 55109 | 55117 | 55127 | 55147 | 55163 | 55171 | 55201 | 55207 | 55213 | 55217 | 55219 | 55229 | 55243 | 55249 | 55259 | 55291 | 55313 | 55331 | 55333 | 55337 |
| 55339 | 55343 | 55351 | 55373 | 55381 | 55399 | 55411 | 55439 | 55441 | 55457 | 55469 | 55487 | 55501 | 55511 | 55529 | 55541 | 55547 | 55579 | 55589 | 55603 |
| 55609 | 55619 | 55621 | 55631 | 55633 | 55639 | 55661 | 55663 | 55667 | 55673 | 55681 | 55691 | 55697 | 55711 | 55717 | 55721 | 55733 | 55763 | 55787 | 55793 |
| 55799 | 55807 | 55813 | 55817 | 55819 | 55823 | 55829 | 55837 | 55843 | 55849 | 55871 | 55889 | 55897 | 55901 | 55903 | 55921 | 55927 | 55931 | 55933 | 55949 |
| 55967 | 55987 | 55997 | 56003 | 56009 | 56039 | 56041 | 56053 | 56081 | 56087 | 56093 | 56099 | 56101 | 56113 | 56123 | 56131 | 56149 | 56167 | 56171 | 56179 |
| 56197 | 56207 | 56209 | 56237 | 56239 | 56249 | 56263 | 56267 | 56269 | 56299 | 56311 | 56333 | 56359 | 56369 | 56377 | 56383 | 56393 | 56401 | 56417 | 56431 |
| 56437 | 56443 | 56453 | 56467 | 56473 | 56477 | 56479 | 56489 | 56501 | 56503 | 56509 | 56519 | 56527 | 56531 | 56533 | 56543 | 56569 | 56591 | 56597 | 56599 |
| 56611 | 56629 | 56633 | 56659 | 56663 | 56671 | 56681 | 56687 | 56701 | 56711 | 56713 | 56731 | 56737 | 56747 | 56767 | 56773 | 56779 | 56783 | 56807 | 56809 |
| 56813 | 56821 | 56827 | 56843 | 56857 | 56873 | 56891 | 56893 | 56897 | 56909 | 56911 | 56921 | 56923 | 56929 | 56941 | 56951 | 56957 | 56963 | 56983 | 56989 |
| 56993 | 56999 | 57037 | 57041 | 57047 | 57059 | 57073 | 57077 | 57089 | 57097 | 57107 | 57119 | 57131 | 57139 | 57143 | 57149 | 57163 | 57173 | 57179 | 57191 |
| 57193 | 57203 | 57221 | 57223 | 57241 | 57251 | 57259 | 57269 | 57271 | 57283 | 57287 | 57301 | 57329 | 57331 | 57347 | 57349 | 57367 | 57373 | 57383 | 57389 |
| 57397 | 57413 | 57427 | 57457 | 57467 | 57487 | 57493 | 57503 | 57527 | 57529 | 57557 | 57559 | 57571 | 57587 | 57593 | 57601 | 57637 | 57641 | 57649 | 57653 |
| 57667 | 57679 | 57689 | 57697 | 57709 | 57713 | 57719 | 57727 | 57731 | 57737 | 57751 | 57773 | 57781 | 57787 | 57791 | 57793 | 57803 | 57809 | 57829 | 57839 |
| 57847 | 57853 | 57859 | 57881 | 57899 | 57901 | 57917 | 57923 | 57943 | 57947 | 57973 | 57977 | 57991 | 58013 | 58027 | 58031 | 58043 | 58049 | 58057 | 58061 |
| 58067 | 58073 | 58099 | 58109 | 58111 | 58129 | 58147 | 58151 | 58153 | 58169 | 58171 | 58189 | 58193 | 58199 | 58207 | 58211 | 58217 | 58229 | 58231 | 58237 |
| 58243 | 58271 | 58309 | 58313 | 58321 | 58337 | 58363 | 58367 | 58369 | 58379 | 58391 | 58393 | 58403 | 58411 | 58417 | 58427 | 58439 | 58441 | 58451 | 58453 |
| 58477 | 58481 | 58511 | 58537 | 58543 | 58549 | 58567 | 58573 | 58579 | 58601 | 58603 | 58613 | 58631 | 58657 | 58661 | 58679 | 58687 | 58693 | 58699 | 58711 |
| 58727 | 58733 | 58741 | 58757 | 58763 | 58771 | 58787 | 58789 | 58831 | 58889 | 58897 | 58901 | 58907 | 58909 | 58913 | 58921 | 58937 | 58943 | 58963 | 58967 |
| 58979 | 58991 | 58997 | 59009 | 59011 | 59021 | 59023 | 59029 | 59051 | 59053 | 59063 | 59069 | 59077 | 59083 | 59093 | 59107 | 59113 | 59119 | 59123 | 59141 |
| 59149 | 59159 | 59167 | 59183 | 59197 | 59207 | 59209 | 59219 | 59221 | 59233 | 59239 | 59243 | 59263 | 59273 | 59281 | 59333 | 59341 | 59351 | 59357 | 59359 |
| 59369 | 59377 | 59387 | 59393 | 59399 | 59407 | 59417 | 59419 | 59441 | 59443 | 59447 | 59453 | 59467 | 59471 | 59473 | 59497 | 59509 | 59513 | 59539 | 59557 |
| 59561 | 59567 | 59581 | 59611 | 59617 | 59621 | 59627 | 59629 | 59651 | 59659 | 59663 | 59669 | 59671 | 59693 | 59699 | 59707 | 59723 | 59729 | 59743 | 59747 |
| 59753 | 59771 | 59779 | 59791 | 59797 | 59809 | 59833 | 59863 | 59879 | 59887 | 59921 | 59929 | 59951 | 59957 | 59971 | 59981 | 59999 | 60013 | 60017 | 60029 |
| 60037 | 60041 | 60077 | 60083 | 60089 | 60091 | 60101 | 60103 | 60107 | 60127 | 60133 | 60139 | 60149 | 60161 | 60167 | 60169 | 60209 | 60217 | 60223 | 60251 |
| 60257 | 60259 | 60271 | 60289 | 60293 | 60317 | 60331 | 60337 | 60343 | 60353 | 60373 | 60383 | 60397 | 60413 | 60427 | 60443 | 60449 | 60457 | 60493 | 60497 |
| 60509 | 60521 | 60527 | 60539 | 60589 | 60601 | 60607 | 60611 | 60617 | 60623 | 60631 | 60637 | 60647 | 60649 | 60659 | 60661 | 60679 | 60689 | 60703 | 60719 |
| 60727 | 60733 | 60737 | 60757 | 60761 | 60763 | 60773 | 60779 | 60793 | 60811 | 60821 | 60859 | 60869 | 60887 | 60889 | 60899 | 60901 | 60913 | 60917 | 60919 |
| 60923 | 60937 | 60943 | 60953 | 60961 | 61001 | 61007 | 61027 | 61031 | 61043 | 61051 | 61057 | 61091 | 61099 | 61121 | 61129 | 61141 | 61151 | 61153 | 61169 |
| 61211 | 61223 | 61231 | 61253 | 61261 | 61283 | 61291 | 61297 | 61331 | 61333 | 61339 | 61343 | 61357 | 61363 | 61379 | 61381 | 61403 | 61409 | 61417 | 61441 |
| 61463 | 61469 | 61471 | 61483 | 61487 | 61493 | 61507 | 61511 | 61519 | 61543 | 61547 | 61553 | 61559 | 61561 | 61583 | 61603 | 61609 | 61613 | 61627 | 61631 |
| 61637 | 61643 | 61651 | 61657 | 61667 | 61673 | 61681 | 61687 | 61703 | 61717 | 61723 | 61729 | 61751 | 61757 | 61781 | 61813 | 61819 | 61837 | 61843 | 61861 |
| 61871 | 61879 | 61909 | 61927 | 61933 | 61949 | 61961 | 61967 | 61979 | 61981 | 61987 | 61991 | 62003 | 62011 | 62017 | 62039 | 62047 | 62053 | 62057 | 62071 |
| 62081 | 62099 | 62119 | 62129 | 62131 | 62137 | 62141 | 62143 | 62171 | 62189 | 62191 | 62201 | 62207 | 62213 | 62219 | 62233 | 62273 | 62297 | 62299 | 62303 |
| 62311 | 62323 | 62327 | 62347 | 62351 | 62383 | 62401 | 62417 | 62423 | 62459 | 62467 | 62473 | 62477 | 62483 | 62497 | 62501 | 62507 | 62533 | 62539 | 62549 |
| 62563 | 62581 | 62591 | 62597 | 62603 | 62617 | 62627 | 62633 | 62639 | 62653 | 62659 | 62683 | 62687 | 62701 | 62723 | 62731 | 62743 | 62753 | 62761 | 62773 |
| 62791 | 62801 | 62819 | 62827 | 62851 | 62861 | 62869 | 62873 | 62897 | 62903 | 62921 | 62927 | 62929 | 62939 | 62969 | 62971 | 62981 | 62983 | 62987 | 62989 |
| 63029 | 63031 | 63059 | 63067 | 63073 | 63079 | 63097 | 63103 | 63113 | 63127 | 63131 | 63149 | 63179 | 63197 | 63199 | 63211 | 63241 | 63247 | 63277 | 63281 |
| 63299 | 63311 | 63313 | 63317 | 63331 | 63337 | 63347 | 63353 | 63361 | 63367 | 63377 | 63389 | 63391 | 63397 | 63409 | 63419 | 63421 | 63439 | 63443 | 63463 |
| 63467 | 63473 | 63487 | 63493 | 63499 | 63521 | 63527 | 63533 | 63541 | 63559 | 63577 | 63587 | 63589 | 63599 | 63601 | 63607 | 63611 | 63617 | 63629 | 63647 |
| 63649 | 63659 | 63667 | 63671 | 63689 | 63691 | 63697 | 63703 | 63709 | 63719 | 63727 | 63737 | 63743 | 63761 | 63773 | 63781 | 63793 | 63799 | 63803 | 63809 |
| 63823 | 63839 | 63841 | 63853 | 63857 | 63863 | 63901 | 63907 | 63913 | 63929 | 63949 | 63977 | 63997 | 64007 | 64013 | 64019 | 64033 | 64037 | 64063 | 64067 |
| 64081 | 64091 | 64109 | 64123 | 64151 | 64153 | 64157 | 64171 | 64187 | 64189 | 64217 | 64223 | 64231 | 64237 | 64271 | 64279 | 64283 | 64301 | 64303 | 64319 |
| 64327 | 64333 | 64373 | 64381 | 64399 | 64403 | 64433 | 64439 | 64451 | 64453 | 64483 | 64489 | 64499 | 64513 | 64553 | 64567 | 64577 | 64579 | 64591 | 64601 |
| 64609 | 64613 | 64621 | 64627 | 64633 | 64661 | 64663 | 64667 | 64679 | 64693 | 64709 | 64717 | 64747 | 64763 | 64781 | 64783 | 64793 | 64811 | 64817 | 64849 |
| 64853 | 64871 | 64877 | 64879 | 64891 | 64901 | 64919 | 64921 | 64927 | 64937 | 64951 | 64969 | 64997 | 65003 | 65011 | 65027 | 65029 | 65033 | 65053 | 65063 |
| 65071 | 65089 | 65099 | 65101 | 65111 | 65119 | 65123 | 65129 | 65141 | 65147 | 65167 | 65171 | 65173 | 65179 | 65183 | 65203 | 65213 | 65239 | 65257 | 65267 |
| 65269 | 65287 | 65293 | 65309 | 65323 | 65327 | 65353 | 65357 | 65371 | 65381 | 65393 | 65407 | 65413 | 65419 | 65423 | 65437 | 65447 | 65449 | 65479 | 65497 |
| 65519 | 65521 | 65537 | 65539 | 65543 | 65551 | 65557 | 65563 | 65579 | 65581 | 65587 | 65599 | 65609 | 65617 | 65629 | 65633 | 65647 | 65651 | 65657 | 65677 |
| 65687 | 65699 | 65701 | 65707 | 65713 | 65717 | 65719 | 65729 | 65731 | 65761 | 65777 | 65789 | 65809 | 65827 | 65831 | 65837 | 65839 | 65843 | 65851 | 65867 |
| 65881 | 65899 | 65921 | 65927 | 65929 | 65951 | 65957 | 65963 | 65981 | 65983 | 65993 | 66029 | 66037 | 66041 | 66047 | 66067 | 66071 | 66083 | 66089 | 66103 |
| 66107 | 66109 | 66137 | 66161 | 66169 | 66173 | 66179 | 66191 | 66221 | 66239 | 66271 | 66293 | 66301 | 66337 | 66343 | 66347 | 66359 | 66361 | 66373 | 66377 |
| 66383 | 66403 | 66413 | 66431 | 66449 | 66457 | 66463 | 66467 | 66491 | 66499 | 66509 | 66523 | 66529 | 66533 | 66541 | 66553 | 66569 | 66571 | 66587 | 66593 |
| 66601 | 66617 | 66629 | 66643 | 66653 | 66683 | 66697 | 66701 | 66713 | 66721 | 66733 | 66739 | 66749 | 66751 | 66763 | 66791 | 66797 | 66809 | 66821 | 66841 |
| 66851 | 66853 | 66863 | 66877 | 66883 | 66889 | 66919 | 66923 | 66931 | 66943 | 66947 | 66949 | 66959 | 66973 | 66977 | 67003 | 67021 | 67033 | 67043 | 67049 |
| 67057 | 67061 | 67073 | 67079 | 67103 | 67121 | 67129 | 67139 | 67141 | 67153 | 67157 | 67169 | 67181 | 67187 | 67189 | 67211 | 67213 | 67217 | 67219 | 67231 |
| 67247 | 67261 | 67271 | 67273 | 67289 | 67307 | 67339 | 67343 | 67349 | 67369 | 67391 | 67399 | 67409 | 67411 | 67421 | 67427 | 67429 | 67433 | 67447 | 67453 |
| 67477 | 67481 | 67489 | 67493 | 67499 | 67511 | 67523 | 67531 | 67537 | 67547 | 67559 | 67567 | 67577 | 67579 | 67589 | 67601 | 67607 | 67619 | 67631 | 67651 |
| 67679 | 67699 | 67709 | 67723 | 67733 | 67741 | 67751 | 67757 | 67759 | 67763 | 67777 | 67783 | 67789 | 67801 | 67807 | 67819 | 67829 | 67843 | 67853 | 67867 |
| 67883 | 67891 | 67901 | 67927 | 67931 | 67933 | 67939 | 67943 | 67957 | 67961 | 67967 | 67979 | 67987 | 67993 | 68023 | 68041 | 68053 | 68059 | 68071 | 68087 |
| 68099 | 68111 | 68113 | 68141 | 68147 | 68161 | 68171 | 68207 | 68209 | 68213 | 68219 | 68227 | 68239 | 68261 | 68279 | 68281 | 68311 | 68329 | 68351 | 68371 |
| 68389 | 68399 | 68437 | 68443 | 68447 | 68449 | 68473 | 68477 | 68483 | 68489 | 68491 | 68501 | 68507 | 68521 | 68531 | 68539 | 68543 | 68567 | 68581 | 68597 |
| 68611 | 68633 | 68639 | 68659 | 68669 | 68683 | 68687 | 68699 | 68711 | 68713 | 68729 | 68737 | 68743 | 68749 | 68767 | 68771 | 68777 | 68791 | 68813 | 68819 |
| 68821 | 68863 | 68879 | 68881 | 68891 | 68897 | 68899 | 68903 | 68909 | 68917 | 68927 | 68947 | 68963 | 68993 | 69001 | 69011 | 69019 | 69029 | 69031 | 69061 |
| 69067 | 69073 | 69109 | 69119 | 69127 | 69143 | 69149 | 69151 | 69163 | 69191 | 69193 | 69197 | 69203 | 69221 | 69233 | 69239 | 69247 | 69257 | 69259 | 69263 |
| 69313 | 69317 | 69337 | 69341 | 69371 | 69379 | 69383 | 69389 | 69401 | 69403 | 69427 | 69431 | 69439 | 69457 | 69463 | 69467 | 69473 | 69481 | 69491 | 69493 |
| 69497 | 69499 | 69539 | 69557 | 69593 | 69623 | 69653 | 69661 | 69677 | 69691 | 69697 | 69709 | 69737 | 69739 | 69761 | 69763 | 69767 | 69779 | 69809 | 69821 |
| 69827 | 69829 | 69833 | 69847 | 69857 | 69859 | 69877 | 69899 | 69911 | 69929 | 69931 | 69941 | 69959 | 69991 | 69997 | 70001 | 70003 | 70009 | 70019 | 70039 |
| 70051 | 70061 | 70067 | 70079 | 70099 | 70111 | 70117 | 70121 | 70123 | 70139 | 70141 | 70157 | 70163 | 70177 | 70181 | 70183 | 70199 | 70201 | 70207 | 70223 |
| 70229 | 70237 | 70241 | 70249 | 70271 | 70289 | 70297 | 70309 | 70313 | 70321 | 70327 | 70351 | 70373 | 70379 | 70381 | 70393 | 70423 | 70429 | 70439 | 70451 |
| 70457 | 70459 | 70481 | 70487 | 70489 | 70501 | 70507 | 70529 | 70537 | 70549 | 70571 | 70573 | 70583 | 70589 | 70607 | 70619 | 70621 | 70627 | 70639 | 70657 |
| 70663 | 70667 | 70687 | 70709 | 70717 | 70729 | 70753 | 70769 | 70783 | 70793 | 70823 | 70841 | 70843 | 70849 | 70853 | 70867 | 70877 | 70879 | 70891 | 70901 |
| 70913 | 70919 | 70921 | 70937 | 70949 | 70951 | 70957 | 70969 | 70979 | 70981 | 70991 | 70997 | 70999 | 71011 | 71023 | 71039 | 71059 | 71069 | 71081 | 71089 |
| 71119 | 71129 | 71143 | 71147 | 71153 | 71161 | 71167 | 71171 | 71191 | 71209 | 71233 | 71237 | 71249 | 71257 | 71261 | 71263 | 71287 | 71293 | 71317 | 71327 |
| 71329 | 71333 | 71339 | 71341 | 71347 | 71353 | 71359 | 71363 | 71387 | 71389 | 71399 | 71411 | 71413 | 71419 | 71429 | 71437 | 71443 | 71453 | 71471 | 71473 |
| 71479 | 71483 | 71503 | 71527 | 71537 | 71549 | 71551 | 71563 | 71569 | 71593 | 71597 | 71633 | 71647 | 71663 | 71671 | 71693 | 71699 | 71707 | 71711 | 71713 |
| 71719 | 71741 | 71761 | 71777 | 71789 | 71807 | 71809 | 71821 | 71837 | 71843 | 71849 | 71861 | 71867 | 71879 | 71881 | 71887 | 71899 | 71909 | 71917 | 71933 |
| 71941 | 71947 | 71963 | 71971 | 71983 | 71987 | 71993 | 71999 | 72019 | 72031 | 72043 | 72047 | 72053 | 72073 | 72077 | 72089 | 72091 | 72101 | 72103 | 72109 |
| 72139 | 72161 | 72167 | 72169 | 72173 | 72211 | 72221 | 72223 | 72227 | 72229 | 72251 | 72253 | 72269 | 72271 | 72277 | 72287 | 72307 | 72313 | 72337 | 72341 |
| 72353 | 72367 | 72379 | 72383 | 72421 | 72431 | 72461 | 72467 | 72469 | 72481 | 72493 | 72497 | 72503 | 72533 | 72547 | 72551 | 72559 | 72577 | 72613 | 72617 |
| 72623 | 72643 | 72647 | 72649 | 72661 | 72671 | 72673 | 72679 | 72689 | 72701 | 72707 | 72719 | 72727 | 72733 | 72739 | 72763 | 72767 | 72797 | 72817 | 72823 |
| 72859 | 72869 | 72871 | 72883 | 72889 | 72893 | 72901 | 72907 | 72911 | 72923 | 72931 | 72937 | 72949 | 72953 | 72959 | 72973 | 72977 | 72997 | 73009 | 73013 |
| 73019 | 73037 | 73039 | 73043 | 73061 | 73063 | 73079 | 73091 | 73121 | 73127 | 73133 | 73141 | 73181 | 73189 | 73237 | 73243 | 73259 | 73277 | 73291 | 73303 |
| 73309 | 73327 | 73331 | 73351 | 73361 | 73363 | 73369 | 73379 | 73387 | 73417 | 73421 | 73433 | 73453 | 73459 | 73471 | 73477 | 73483 | 73517 | 73523 | 73529 |
| 73547 | 73553 | 73561 | 73571 | 73583 | 73589 | 73597 | 73607 | 73609 | 73613 | 73637 | 73643 | 73651 | 73673 | 73679 | 73681 | 73693 | 73699 | 73709 | 73721 |
| 73727 | 73751 | 73757 | 73771 | 73783 | 73819 | 73823 | 73847 | 73849 | 73859 | 73867 | 73877 | 73883 | 73897 | 73907 | 73939 | 73943 | 73951 | 73961 | 73973 |
| 73999 | 74017 | 74021 | 74027 | 74047 | 74051 | 74071 | 74077 | 74093 | 74099 | 74101 | 74131 | 74143 | 74149 | 74159 | 74161 | 74167 | 74177 | 74189 | 74197 |
| 74201 | 74203 | 74209 | 74219 | 74231 | 74257 | 74279 | 74287 | 74293 | 74297 | 74311 | 74317 | 74323 | 74353 | 74357 | 74363 | 74377 | 74381 | 74383 | 74411 |
| 74413 | 74419 | 74441 | 74449 | 74453 | 74471 | 74489 | 74507 | 74509 | 74521 | 74527 | 74531 | 74551 | 74561 | 74567 | 74573 | 74587 | 74597 | 74609 | 74611 |
| 74623 | 74653 | 74687 | 74699 | 74707 | 74713 | 74717 | 74719 | 74729 | 74731 | 74747 | 74759 | 74761 | 74771 | 74779 | 74797 | 74821 | 74827 | 74831 | 74843 |
| 74857 | 74861 | 74869 | 74873 | 74887 | 74891 | 74897 | 74903 | 74923 | 74929 | 74933 | 74941 | 74959 | 75011 | 75013 | 75017 | 75029 | 75037 | 75041 | 75079 |
| 75083 | 75109 | 75133 | 75149 | 75161 | 75167 | 75169 | 75181 | 75193 | 75209 | 75211 | 75217 | 75223 | 75227 | 75239 | 75253 | 75269 | 75277 | 75289 | 75307 |
| 75323 | 75329 | 75337 | 75347 | 75353 | 75367 | 75377 | 75389 | 75391 | 75401 | 75403 | 75407 | 75431 | 75437 | 75479 | 75503 | 75511 | 75521 | 75527 | 75533 |
| 75539 | 75541 | 75553 | 75557 | 75571 | 75577 | 75583 | 75611 | 75617 | 75619 | 75629 | 75641 | 75653 | 75659 | 75679 | 75683 | 75689 | 75703 | 75707 | 75709 |
| 75721 | 75731 | 75743 | 75767 | 75773 | 75781 | 75787 | 75793 | 75797 | 75821 | 75833 | 75853 | 75869 | 75883 | 75913 | 75931 | 75937 | 75941 | 75967 | 75979 |
| 75983 | 75989 | 75991 | 75997 | 76001 | 76003 | 76031 | 76039 | 76079 | 76081 | 76091 | 76099 | 76103 | 76123 | 76129 | 76147 | 76157 | 76159 | 76163 | 76207 |
| 76213 | 76231 | 76243 | 76249 | 76253 | 76259 | 76261 | 76283 | 76289 | 76303 | 76333 | 76343 | 76367 | 76369 | 76379 | 76387 | 76403 | 76421 | 76423 | 76441 |
| 76463 | 76471 | 76481 | 76487 | 76493 | 76507 | 76511 | 76519 | 76537 | 76541 | 76543 | 76561 | 76579 | 76597 | 76603 | 76607 | 76631 | 76649 | 76651 | 76667 |
| 76673 | 76679 | 76697 | 76717 | 76733 | 76753 | 76757 | 76771 | 76777 | 76781 | 76801 | 76819 | 76829 | 76831 | 76837 | 76847 | 76871 | 76873 | 76883 | 76907 |
| 76913 | 76919 | 76943 | 76949 | 76961 | 76963 | 76991 | 77003 | 77017 | 77023 | 77029 | 77041 | 77047 | 77069 | 77081 | 77093 | 77101 | 77137 | 77141 | 77153 |
| 77167 | 77171 | 77191 | 77201 | 77213 | 77237 | 77239 | 77243 | 77249 | 77261 | 77263 | 77267 | 77269 | 77279 | 77291 | 77317 | 77323 | 77339 | 77347 | 77351 |
| 77359 | 77369 | 77377 | 77383 | 77417 | 77419 | 77431 | 77447 | 77471 | 77477 | 77479 | 77489 | 77491 | 77509 | 77513 | 77521 | 77527 | 77543 | 77549 | 77551 |
| 77557 | 77563 | 77569 | 77573 | 77587 | 77591 | 77611 | 77617 | 77621 | 77641 | 77647 | 77659 | 77681 | 77687 | 77689 | 77699 | 77711 | 77713 | 77719 | 77723 |
| 77731 | 77743 | 77747 | 77761 | 77773 | 77783 | 77797 | 77801 | 77813 | 77839 | 77849 | 77863 | 77867 | 77893 | 77899 | 77929 | 77933 | 77951 | 77969 | 77977 |
| 77983 | 77999 | 78007 | 78017 | 78031 | 78041 | 78049 | 78059 | 78079 | 78101 | 78121 | 78137 | 78139 | 78157 | 78163 | 78167 | 78173 | 78179 | 78191 | 78193 |
| 78203 | 78229 | 78233 | 78241 | 78259 | 78277 | 78283 | 78301 | 78307 | 78311 | 78317 | 78341 | 78347 | 78367 | 78401 | 78427 | 78437 | 78439 | 78467 | 78479 |
| 78487 | 78497 | 78509 | 78511 | 78517 | 78539 | 78541 | 78553 | 78569 | 78571 | 78577 | 78583 | 78593 | 78607 | 78623 | 78643 | 78649 | 78653 | 78691 | 78697 |
| 78707 | 78713 | 78721 | 78737 | 78779 | 78781 | 78787 | 78791 | 78797 | 78803 | 78809 | 78823 | 78839 | 78853 | 78857 | 78877 | 78887 | 78889 | 78893 | 78901 |
| 78919 | 78929 | 78941 | 78977 | 78979 | 78989 | 79031 | 79039 | 79043 | 79063 | 79087 | 79103 | 79111 | 79133 | 79139 | 79147 | 79151 | 79153 | 79159 | 79181 |
| 79187 | 79193 | 79201 | 79229 | 79231 | 79241 | 79259 | 79273 | 79279 | 79283 | 79301 | 79309 | 79319 | 79333 | 79337 | 79349 | 79357 | 79367 | 79379 | 79393 |
| 79397 | 79399 | 79411 | 79423 | 79427 | 79433 | 79451 | 79481 | 79493 | 79531 | 79537 | 79549 | 79559 | 79561 | 79579 | 79589 | 79601 | 79609 | 79613 | 79621 |
| 79627 | 79631 | 79633 | 79657 | 79669 | 79687 | 79691 | 79693 | 79697 | 79699 | 79757 | 79769 | 79777 | 79801 | 79811 | 79813 | 79817 | 79823 | 79829 | 79841 |
| 79843 | 79847 | 79861 | 79867 | 79873 | 79889 | 79901 | 79903 | 79907 | 79939 | 79943 | 79967 | 79973 | 79979 | 79987 | 79997 | 79999 | 80021 | 80039 | 80051 |
| 80071 | 80077 | 80107 | 80111 | 80141 | 80147 | 80149 | 80153 | 80167 | 80173 | 80177 | 80191 | 80207 | 80209 | 80221 | 80231 | 80233 | 80239 | 80251 | 80263 |
| 80273 | 80279 | 80287 | 80309 | 80317 | 80329 | 80341 | 80347 | 80363 | 80369 | 80387 | 80407 | 80429 | 80447 | 80449 | 80471 | 80473 | 80489 | 80491 | 80513 |
| 80527 | 80537 | 80557 | 80567 | 80599 | 80603 | 80611 | 80621 | 80627 | 80629 | 80651 | 80657 | 80669 | 80671 | 80677 | 80681 | 80683 | 80687 | 80701 | 80713 |
| 80737 | 80747 | 80749 | 80761 | 80777 | 80779 | 80783 | 80789 | 80803 | 80809 | 80819 | 80831 | 80833 | 80849 | 80863 | 80897 | 80909 | 80911 | 80917 | 80923 |
| 80929 | 80933 | 80953 | 80963 | 80989 | 81001 | 81013 | 81017 | 81019 | 81023 | 81031 | 81041 | 81043 | 81047 | 81049 | 81071 | 81077 | 81083 | 81097 | 81101 |
| 81119 | 81131 | 81157 | 81163 | 81173 | 81181 | 81197 | 81199 | 81203 | 81223 | 81233 | 81239 | 81281 | 81283 | 81293 | 81299 | 81307 | 81331 | 81343 | 81349 |
| 81353 | 81359 | 81371 | 81373 | 81401 | 81409 | 81421 | 81439 | 81457 | 81463 | 81509 | 81517 | 81527 | 81533 | 81547 | 81551 | 81553 | 81559 | 81563 | 81569 |
| 81611 | 81619 | 81629 | 81637 | 81647 | 81649 | 81667 | 81671 | 81677 | 81689 | 81701 | 81703 | 81707 | 81727 | 81737 | 81749 | 81761 | 81769 | 81773 | 81799 |
| 81817 | 81839 | 81847 | 81853 | 81869 | 81883 | 81899 | 81901 | 81919 | 81929 | 81931 | 81937 | 81943 | 81953 | 81967 | 81971 | 81973 | 82003 | 82007 | 82009 |
| 82013 | 82021 | 82031 | 82037 | 82039 | 82051 | 82067 | 82073 | 82129 | 82139 | 82141 | 82153 | 82163 | 82171 | 82183 | 82189 | 82193 | 82207 | 82217 | 82219 |
| 82223 | 82231 | 82237 | 82241 | 82261 | 82267 | 82279 | 82301 | 82307 | 82339 | 82349 | 82351 | 82361 | 82373 | 82387 | 82393 | 82421 | 82457 | 82463 | 82469 |
| 82471 | 82483 | 82487 | 82493 | 82499 | 82507 | 82529 | 82531 | 82549 | 82559 | 82561 | 82567 | 82571 | 82591 | 82601 | 82609 | 82613 | 82619 | 82633 | 82651 |
| 82657 | 82699 | 82721 | 82723 | 82727 | 82729 | 82757 | 82759 | 82763 | 82781 | 82787 | 82793 | 82799 | 82811 | 82813 | 82837 | 82847 | 82883 | 82889 | 82891 |
| 82903 | 82913 | 82939 | 82963 | 82981 | 82997 | 83003 | 83009 | 83023 | 83047 | 83059 | 83063 | 83071 | 83077 | 83089 | 83093 | 83101 | 83117 | 83137 | 83177 |
| 83203 | 83207 | 83219 | 83221 | 83227 | 83231 | 83233 | 83243 | 83257 | 83267 | 83269 | 83273 | 83299 | 83311 | 83339 | 83341 | 83357 | 83383 | 83389 | 83399 |
| 83401 | 83407 | 83417 | 83423 | 83431 | 83437 | 83443 | 83449 | 83459 | 83471 | 83477 | 83497 | 83537 | 83557 | 83561 | 83563 | 83579 | 83591 | 83597 | 83609 |
| 83617 | 83621 | 83639 | 83641 | 83653 | 83663 | 83689 | 83701 | 83717 | 83719 | 83737 | 83761 | 83773 | 83777 | 83791 | 83813 | 83833 | 83843 | 83857 | 83869 |
| 83873 | 83891 | 83903 | 83911 | 83921 | 83933 | 83939 | 83969 | 83983 | 83987 | 84011 | 84017 | 84047 | 84053 | 84059 | 84061 | 84067 | 84089 | 84121 | 84127 |
| 84131 | 84137 | 84143 | 84163 | 84179 | 84181 | 84191 | 84199 | 84211 | 84221 | 84223 | 84229 | 84239 | 84247 | 84263 | 84299 | 84307 | 84313 | 84317 | 84319 |
| 84347 | 84349 | 84377 | 84389 | 84391 | 84401 | 84407 | 84421 | 84431 | 84437 | 84443 | 84449 | 84457 | 84463 | 84467 | 84481 | 84499 | 84503 | 84509 | 84521 |
| 84523 | 84533 | 84551 | 84559 | 84589 | 84629 | 84631 | 84649 | 84653 | 84659 | 84673 | 84691 | 84697 | 84701 | 84713 | 84719 | 84731 | 84737 | 84751 | 84761 |
| 84787 | 84793 | 84809 | 84811 | 84827 | 84857 | 84859 | 84869 | 84871 | 84913 | 84919 | 84947 | 84961 | 84967 | 84977 | 84979 | 84991 | 85009 | 85021 | 85027 |
| 85037 | 85049 | 85061 | 85081 | 85087 | 85091 | 85093 | 85103 | 85109 | 85121 | 85133 | 85147 | 85159 | 85193 | 85199 | 85201 | 85213 | 85223 | 85229 | 85237 |
| 85243 | 85247 | 85259 | 85297 | 85303 | 85313 | 85331 | 85333 | 85361 | 85363 | 85369 | 85381 | 85411 | 85427 | 85429 | 85439 | 85447 | 85451 | 85453 | 85469 |
| 85487 | 85513 | 85517 | 85523 | 85531 | 85549 | 85571 | 85577 | 85597 | 85601 | 85607 | 85619 | 85621 | 85627 | 85639 | 85643 | 85661 | 85667 | 85669 | 85691 |
| 85703 | 85711 | 85717 | 85733 | 85751 | 85781 | 85793 | 85817 | 85819 | 85829 | 85831 | 85837 | 85843 | 85847 | 85853 | 85889 | 85903 | 85909 | 85931 | 85933 |
| 85991 | 85999 | 86011 | 86017 | 86027 | 86029 | 86069 | 86077 | 86083 | 86111 | 86113 | 86117 | 86131 | 86137 | 86143 | 86161 | 86171 | 86179 | 86183 | 86197 |
| 86201 | 86209 | 86239 | 86243 | 86249 | 86257 | 86263 | 86269 | 86287 | 86291 | 86293 | 86297 | 86311 | 86323 | 86341 | 86351 | 86353 | 86357 | 86369 | 86371 |
| 86381 | 86389 | 86399 | 86413 | 86423 | 86441 | 86453 | 86461 | 86467 | 86477 | 86491 | 86501 | 86509 | 86531 | 86533 | 86539 | 86561 | 86573 | 86579 | 86587 |
| 86599 | 86627 | 86629 | 86677 | 86689 | 86693 | 86711 | 86719 | 86729 | 86743 | 86753 | 86767 | 86771 | 86783 | 86813 | 86837 | 86843 | 86851 | 86857 | 86861 |
| 86869 | 86923 | 86927 | 86929 | 86939 | 86951 | 86959 | 86969 | 86981 | 86993 | 87011 | 87013 | 87037 | 87041 | 87049 | 87071 | 87083 | 87103 | 87107 | 87119 |
| 87121 | 87133 | 87149 | 87151 | 87179 | 87181 | 87187 | 87211 | 87221 | 87223 | 87251 | 87253 | 87257 | 87277 | 87281 | 87293 | 87299 | 87313 | 87317 | 87323 |
| 87337 | 87359 | 87383 | 87403 | 87407 | 87421 | 87427 | 87433 | 87443 | 87473 | 87481 | 87491 | 87509 | 87511 | 87517 | 87523 | 87539 | 87541 | 87547 | 87553 |
| 87557 | 87559 | 87583 | 87587 | 87589 | 87613 | 87623 | 87629 | 87631 | 87641 | 87643 | 87649 | 87671 | 87679 | 87683 | 87691 | 87697 | 87701 | 87719 | 87721 |
| 87739 | 87743 | 87751 | 87767 | 87793 | 87797 | 87803 | 87811 | 87833 | 87853 | 87869 | 87877 | 87881 | 87887 | 87911 | 87917 | 87931 | 87943 | 87959 | 87961 |
| 87973 | 87977 | 87991 | 88001 | 88003 | 88007 | 88019 | 88037 | 88069 | 88079 | 88093 | 88117 | 88129 | 88169 | 88177 | 88211 | 88223 | 88237 | 88241 | 88259 |
| 88261 | 88289 | 88301 | 88321 | 88327 | 88337 | 88339 | 88379 | 88397 | 88411 | 88423 | 88427 | 88463 | 88469 | 88471 | 88493 | 88499 | 88513 | 88523 | 88547 |
| 88589 | 88591 | 88607 | 88609 | 88643 | 88651 | 88657 | 88661 | 88663 | 88667 | 88681 | 88721 | 88729 | 88741 | 88747 | 88771 | 88789 | 88793 | 88799 | 88801 |
| 88807 | 88811 | 88813 | 88817 | 88819 | 88843 | 88853 | 88861 | 88867 | 88873 | 88883 | 88897 | 88903 | 88919 | 88937 | 88951 | 88969 | 88993 | 88997 | 89003 |
| 89009 | 89017 | 89021 | 89041 | 89051 | 89057 | 89069 | 89071 | 89083 | 89087 | 89101 | 89107 | 89113 | 89119 | 89123 | 89137 | 89153 | 89189 | 89203 | 89209 |
| 89213 | 89227 | 89231 | 89237 | 89261 | 89269 | 89273 | 89293 | 89303 | 89317 | 89329 | 89363 | 89371 | 89381 | 89387 | 89393 | 89399 | 89413 | 89417 | 89431 |
| 89443 | 89449 | 89459 | 89477 | 89491 | 89501 | 89513 | 89519 | 89521 | 89527 | 89533 | 89561 | 89563 | 89567 | 89591 | 89597 | 89599 | 89603 | 89611 | 89627 |
| 89633 | 89653 | 89657 | 89659 | 89669 | 89671 | 89681 | 89689 | 89753 | 89759 | 89767 | 89779 | 89783 | 89797 | 89809 | 89819 | 89821 | 89833 | 89839 | 89849 |
| 89867 | 89891 | 89897 | 89899 | 89909 | 89917 | 89923 | 89939 | 89959 | 89963 | 89977 | 89983 | 89989 | 90001 | 90007 | 90011 | 90017 | 90019 | 90023 | 90031 |
| 90053 | 90059 | 90067 | 90071 | 90073 | 90089 | 90107 | 90121 | 90127 | 90149 | 90163 | 90173 | 90187 | 90191 | 90197 | 90199 | 90203 | 90217 | 90227 | 90239 |
| 90247 | 90263 | 90271 | 90281 | 90289 | 90313 | 90353 | 90359 | 90371 | 90373 | 90379 | 90397 | 90401 | 90403 | 90407 | 90437 | 90439 | 90469 | 90473 | 90481 |
| 90499 | 90511 | 90523 | 90527 | 90529 | 90533 | 90547 | 90583 | 90599 | 90617 | 90619 | 90631 | 90641 | 90647 | 90659 | 90677 | 90679 | 90697 | 90703 | 90709 |
| 90731 | 90749 | 90787 | 90793 | 90803 | 90821 | 90823 | 90833 | 90841 | 90847 | 90863 | 90887 | 90901 | 90907 | 90911 | 90917 | 90931 | 90947 | 90971 | 90977 |
| 90989 | 90997 | 91009 | 91019 | 91033 | 91079 | 91081 | 91097 | 91099 | 91121 | 91127 | 91129 | 91139 | 91141 | 91151 | 91153 | 91159 | 91163 | 91183 | 91193 |
| 91199 | 91229 | 91237 | 91243 | 91249 | 91253 | 91283 | 91291 | 91297 | 91303 | 91309 | 91331 | 91367 | 91369 | 91373 | 91381 | 91387 | 91393 | 91397 | 91411 |
| 91423 | 91433 | 91453 | 91457 | 91459 | 91463 | 91493 | 91499 | 91513 | 91529 | 91541 | 91571 | 91573 | 91577 | 91583 | 91591 | 91621 | 91631 | 91639 | 91673 |
| 91691 | 91703 | 91711 | 91733 | 91753 | 91757 | 91771 | 91781 | 91801 | 91807 | 91811 | 91813 | 91823 | 91837 | 91841 | 91867 | 91873 | 91909 | 91921 | 91939 |
| 91943 | 91951 | 91957 | 91961 | 91967 | 91969 | 91997 | 92003 | 92009 | 92033 | 92041 | 92051 | 92077 | 92083 | 92107 | 92111 | 92119 | 92143 | 92153 | 92173 |
| 92177 | 92179 | 92189 | 92203 | 92219 | 92221 | 92227 | 92233 | 92237 | 92243 | 92251 | 92269 | 92297 | 92311 | 92317 | 92333 | 92347 | 92353 | 92357 | 92363 |
| 92369 | 92377 | 92381 | 92383 | 92387 | 92399 | 92401 | 92413 | 92419 | 92431 | 92459 | 92461 | 92467 | 92479 | 92489 | 92503 | 92507 | 92551 | 92557 | 92567 |
| 92569 | 92581 | 92593 | 92623 | 92627 | 92639 | 92641 | 92647 | 92657 | 92669 | 92671 | 92681 | 92683 | 92693 | 92699 | 92707 | 92717 | 92723 | 92737 | 92753 |
| 92761 | 92767 | 92779 | 92789 | 92791 | 92801 | 92809 | 92821 | 92831 | 92849 | 92857 | 92861 | 92863 | 92867 | 92893 | 92899 | 92921 | 92927 | 92941 | 92951 |
| 92957 | 92959 | 92987 | 92993 | 93001 | 93047 | 93053 | 93059 | 93077 | 93083 | 93089 | 93097 | 93103 | 93113 | 93131 | 93133 | 93139 | 93151 | 93169 | 93179 |
| 93187 | 93199 | 93229 | 93239 | 93241 | 93251 | 93253 | 93257 | 93263 | 93281 | 93283 | 93287 | 93307 | 93319 | 93323 | 93329 | 93337 | 93371 | 93377 | 93383 |
| 93407 | 93419 | 93427 | 93463 | 93479 | 93481 | 93487 | 93491 | 93493 | 93497 | 93503 | 93523 | 93529 | 93553 | 93557 | 93559 | 93563 | 93581 | 93601 | 93607 |
| 93629 | 93637 | 93683 | 93701 | 93703 | 93719 | 93739 | 93761 | 93763 | 93787 | 93809 | 93811 | 93827 | 93851 | 93871 | 93887 | 93889 | 93893 | 93901 | 93911 |
| 93913 | 93923 | 93937 | 93941 | 93949 | 93967 | 93971 | 93979 | 93983 | 93997 | 94007 | 94009 | 94033 | 94049 | 94057 | 94063 | 94079 | 94099 | 94109 | 94111 |
| 94117 | 94121 | 94151 | 94153 | 94169 | 94201 | 94207 | 94219 | 94229 | 94253 | 94261 | 94273 | 94291 | 94307 | 94309 | 94321 | 94327 | 94331 | 94343 | 94349 |
| 94351 | 94379 | 94397 | 94399 | 94421 | 94427 | 94433 | 94439 | 94441 | 94447 | 94463 | 94477 | 94483 | 94513 | 94529 | 94531 | 94541 | 94543 | 94547 | 94559 |
| 94561 | 94573 | 94583 | 94597 | 94603 | 94613 | 94621 | 94649 | 94651 | 94687 | 94693 | 94709 | 94723 | 94727 | 94747 | 94771 | 94777 | 94781 | 94789 | 94793 |
| 94811 | 94819 | 94823 | 94837 | 94841 | 94847 | 94849 | 94873 | 94889 | 94903 | 94907 | 94933 | 94949 | 94951 | 94961 | 94993 | 94999 | 95003 | 95009 | 95021 |
| 95027 | 95063 | 95071 | 95083 | 95087 | 95089 | 95093 | 95101 | 95107 | 95111 | 95131 | 95143 | 95153 | 95177 | 95189 | 95191 | 95203 | 95213 | 95219 | 95231 |
| 95233 | 95239 | 95257 | 95261 | 95267 | 95273 | 95279 | 95287 | 95311 | 95317 | 95327 | 95339 | 95369 | 95383 | 95393 | 95401 | 95413 | 95419 | 95429 | 95441 |
| 95443 | 95461 | 95467 | 95471 | 95479 | 95483 | 95507 | 95527 | 95531 | 95539 | 95549 | 95561 | 95569 | 95581 | 95597 | 95603 | 95617 | 95621 | 95629 | 95633 |
| 95651 | 95701 | 95707 | 95713 | 95717 | 95723 | 95731 | 95737 | 95747 | 95773 | 95783 | 95789 | 95791 | 95801 | 95803 | 95813 | 95819 | 95857 | 95869 | 95873 |
| 95881 | 95891 | 95911 | 95917 | 95923 | 95929 | 95947 | 95957 | 95959 | 95971 | 95987 | 95989 | 96001 | 96013 | 96017 | 96043 | 96053 | 96059 | 96079 | 96097 |
| 96137 | 96149 | 96157 | 96167 | 96179 | 96181 | 96199 | 96211 | 96221 | 96223 | 96233 | 96259 | 96263 | 96269 | 96281 | 96289 | 96293 | 96323 | 96329 | 96331 |
| 96337 | 96353 | 96377 | 96401 | 96419 | 96431 | 96443 | 96451 | 96457 | 96461 | 96469 | 96479 | 96487 | 96493 | 96497 | 96517 | 96527 | 96553 | 96557 | 96581 |
| 96587 | 96589 | 96601 | 96643 | 96661 | 96667 | 96671 | 96697 | 96703 | 96731 | 96737 | 96739 | 96749 | 96757 | 96763 | 96769 | 96779 | 96787 | 96797 | 96799 |
| 96821 | 96823 | 96827 | 96847 | 96851 | 96857 | 96893 | 96907 | 96911 | 96931 | 96953 | 96959 | 96973 | 96979 | 96989 | 96997 | 97001 | 97003 | 97007 | 97021 |
| 97039 | 97073 | 97081 | 97103 | 97117 | 97127 | 97151 | 97157 | 97159 | 97169 | 97171 | 97177 | 97187 | 97213 | 97231 | 97241 | 97259 | 97283 | 97301 | 97303 |
| 97327 | 97367 | 97369 | 97373 | 97379 | 97381 | 97387 | 97397 | 97423 | 97429 | 97441 | 97453 | 97459 | 97463 | 97499 | 97501 | 97511 | 97523 | 97547 | 97549 |
| 97553 | 97561 | 97571 | 97577 | 97579 | 97583 | 97607 | 97609 | 97613 | 97649 | 97651 | 97673 | 97687 | 97711 | 97729 | 97771 | 97777 | 97787 | 97789 | 97813 |
| 97829 | 97841 | 97843 | 97847 | 97849 | 97859 | 97861 | 97871 | 97879 | 97883 | 97919 | 97927 | 97931 | 97943 | 97961 | 97967 | 97973 | 97987 | 98009 | 98011 |
| 98017 | 98041 | 98047 | 98057 | 98081 | 98101 | 98123 | 98129 | 98143 | 98179 | 98207 | 98213 | 98221 | 98227 | 98251 | 98257 | 98269 | 98297 | 98299 | 98317 |
| 98321 | 98323 | 98327 | 98347 | 98369 | 98377 | 98387 | 98389 | 98407 | 98411 | 98419 | 98429 | 98443 | 98453 | 98459 | 98467 | 98473 | 98479 | 98491 | 98507 |
| 98519 | 98533 | 98543 | 98561 | 98563 | 98573 | 98597 | 98621 | 98627 | 98639 | 98641 | 98663 | 98669 | 98689 | 98711 | 98713 | 98717 | 98729 | 98731 | 98737 |
| 98773 | 98779 | 98801 | 98807 | 98809 | 98837 | 98849 | 98867 | 98869 | 98873 | 98887 | 98893 | 98897 | 98899 | 98909 | 98911 | 98927 | 98929 | 98939 | 98947 |
| 98953 | 98963 | 98981 | 98993 | 98999 | 99013 | 99017 | 99023 | 99041 | 99053 | 99079 | 99083 | 99089 | 99103 | 99109 | 99119 | 99131 | 99133 | 99137 | 99139 |
| 99149 | 99173 | 99181 | 99191 | 99223 | 99233 | 99241 | 99251 | 99257 | 99259 | 99277 | 99289 | 99317 | 99347 | 99349 | 99367 | 99371 | 99377 | 99391 | 99397 |
| 99401 | 99409 | 99431 | 99439 | 99469 | 99487 | 99497 | 99523 | 99527 | 99529 | 99551 | 99559 | 99563 | 99571 | 99577 | 99581 | 99607 | 99611 | 99623 | 99643 |
| 99661 | 99667 | 99679 | 99689 | 99707 | 99709 | 99713 | 99719 | 99721 | 99733 | 99761 | 99767 | 99787 | 99793 | 99809 | 99817 | 99823 | 99829 | 99833 | 99839 |
| 99859 | 99871 | 99877 | 99881 | 99901 | 99907 | 99923 | 99929 | 99961 | 99971 | 99989 | 99991 | 100003 | 100019 | 100043 | 100049 | 100057 | 100069 | 100103 | 100109 |
| 100129 | 100151 | 100153 | 100169 | 100183 | 100189 | 100193 | 100207 | 100213 | 100237 | 100267 | 100271 | 100279 | 100291 | 100297 | 100313 | 100333 | 100343 | 100357 | 100361 |
| 100363 | 100379 | 100391 | 100393 | 100403 | 100411 | 100417 | 100447 | 100459 | 100469 | 100483 | 100493 | 100501 | 100511 | 100517 | 100519 | 100523 | 100537 | 100547 | 100549 |
| 100559 | 100591 | 100609 | 100613 | 100621 | 100649 | 100669 | 100673 | 100693 | 100699 | 100703 | 100733 | 100741 | 100747 | 100769 | 100787 | 100799 | 100801 | 100811 | 100823 |
| 100829 | 100847 | 100853 | 100907 | 100913 | 100927 | 100931 | 100937 | 100943 | 100957 | 100981 | 100987 | 100999 | 101009 | 101021 | 101027 | 101051 | 101063 | 101081 | 101089 |
| 101107 | 101111 | 101113 | 101117 | 101119 | 101141 | 101149 | 101159 | 101161 | 101173 | 101183 | 101197 | 101203 | 101207 | 101209 | 101221 | 101267 | 101273 | 101279 | 101281 |
| 101287 | 101293 | 101323 | 101333 | 101341 | 101347 | 101359 | 101363 | 101377 | 101383 | 101399 | 101411 | 101419 | 101429 | 101449 | 101467 | 101477 | 101483 | 101489 | 101501 |
| 101503 | 101513 | 101527 | 101531 | 101533 | 101537 | 101561 | 101573 | 101581 | 101599 | 101603 | 101611 | 101627 | 101641 | 101653 | 101663 | 101681 | 101693 | 101701 | 101719 |
| 101723 | 101737 | 101741 | 101747 | 101749 | 101771 | 101789 | 101797 | 101807 | 101833 | 101837 | 101839 | 101863 | 101869 | 101873 | 101879 | 101891 | 101917 | 101921 | 101929 |
| 101939 | 101957 | 101963 | 101977 | 101987 | 101999 | 102001 | 102013 | 102019 | 102023 | 102031 | 102043 | 102059 | 102061 | 102071 | 102077 | 102079 | 102101 | 102103 | 102107 |
| 102121 | 102139 | 102149 | 102161 | 102181 | 102191 | 102197 | 102199 | 102203 | 102217 | 102229 | 102233 | 102241 | 102251 | 102253 | 102259 | 102293 | 102299 | 102301 | 102317 |
| 102329 | 102337 | 102359 | 102367 | 102397 | 102407 | 102409 | 102433 | 102437 | 102451 | 102461 | 102481 | 102497 | 102499 | 102503 | 102523 | 102533 | 102539 | 102547 | 102551 |
| 102559 | 102563 | 102587 | 102593 | 102607 | 102611 | 102643 | 102647 | 102653 | 102667 | 102673 | 102677 | 102679 | 102701 | 102761 | 102763 | 102769 | 102793 | 102797 | 102811 |
| 102829 | 102841 | 102859 | 102871 | 102877 | 102881 | 102911 | 102913 | 102929 | 102931 | 102953 | 102967 | 102983 | 103001 | 103007 | 103043 | 103049 | 103067 | 103069 | 103079 |
| 103087 | 103091 | 103093 | 103099 | 103123 | 103141 | 103171 | 103177 | 103183 | 103217 | 103231 | 103237 | 103289 | 103291 | 103307 | 103319 | 103333 | 103349 | 103357 | 103387 |
| 103391 | 103393 | 103399 | 103409 | 103421 | 103423 | 103451 | 103457 | 103471 | 103483 | 103511 | 103529 | 103549 | 103553 | 103561 | 103567 | 103573 | 103577 | 103583 | 103591 |
| 103613 | 103619 | 103643 | 103651 | 103657 | 103669 | 103681 | 103687 | 103699 | 103703 | 103723 | 103769 | 103787 | 103801 | 103811 | 103813 | 103837 | 103841 | 103843 | 103867 |
| 103889 | 103903 | 103913 | 103919 | 103951 | 103963 | 103967 | 103969 | 103979 | 103981 | 103991 | 103993 | 103997 | 104003 | 104009 | 104021 | 104033 | 104047 | 104053 | 104059 |
| 104087 | 104089 | 104107 | 104113 | 104119 | 104123 | 104147 | 104149 | 104161 | 104173 | 104179 | 104183 | 104207 | 104231 | 104233 | 104239 | 104243 | 104281 | 104287 | 104297 |
| 104309 | 104311 | 104323 | 104327 | 104347 | 104369 | 104381 | 104383 | 104393 | 104399 | 104417 | 104459 | 104471 | 104473 | 104479 | 104491 | 104513 | 104527 | 104537 | 104543 |
| 104549 | 104551 | 104561 | 104579 | 104593 | 104597 | 104623 | 104639 | 104651 | 104659 | 104677 | 104681 | 104683 | 104693 | 104701 | 104707 | 104711 | 104717 | 104723 | 104729 |
Código fonte da macro utilizada
[editar | editar código-fonte]Para obter uma réplica da tabela acima, basta fazer o seguinte:
- Criar um novo documento no OpenOffice.org Writer;
- Copiar o código abaixo para uma nova macro do OpenOffice.org Basic.
- Executar a macro escolhendo (quando for perguntado) 500 linhas, 20 colunas e maior número primo igual a 123456.
- Notas
- A execução pode levar alguns minutos (não mais do que 10, para 10.000 primos), pois não foi feito qualquer esforço para otimizar o código.
- No caso de querer converter a tabela resultante para a sintaxe do MediaWiki, pode ser utilizado uma ferramenta para conversão automática. Na Wikipédia inglesa há uma lista de opções disponível na página Wikipedia:Tools.
Public Plan As Object
Sub TabelaDePrimos ()
EscreveTabela (CLng (InputBox ("Quantas linhas:")), CLng (InputBox ("Quantas colunas:")), CLng (InputBox ("Maior número primo permitido:")))
End sub
Sub EscreveTabela (MaxL as Long, MaxC as Long, MaxP)
Dim document as object
Dim dispatcher as object
'Dim Cel As Object
'Plan = ThisComponent.getCurrentController().getActiveSheet()
document = ThisComponent.CurrentController.Frame
dispatcher = createUnoService("com.sun.star.frame.DispatchHelper")
' A palavra "COM" deve ser grafada em minusculo para funcionar.
' O formatador da Wikipedia esta colocando em maiusculo por engano.
dim args1(3) as new com.sun.star.beans.PropertyValue
args1(0).Name = "TableName"
args1(0).Value = ""
args1(1).Name = "Columns"
args1(1).Value = MaxC
args1(2).Name = "Rows"
args1(2).Value = MaxL
dispatcher.executeDispatch(document, ".uno:InsertTable", "", 0, args1())
' A palavra "COM" deve ser grafada em minusculo para funcionar.
' O formatador da Wikipedia esta colocando em maiusculo por engano.
dim args2(0) as new com.sun.star.beans.PropertyValue
N=2
For l=0 To MaxL-1
For c=0 to MaxC-1
Do While Not ePrimo(N)
N=N+1
Loop
If N>MaxP Then Exit Sub
'Escreve na tabela
args2(0).Name = "Text"
args2(0).Value = Str(N)
dispatcher.executeDispatch(document, ".uno:InsertText", "", 0, args2())
dispatcher.executeDispatch(document, ".uno:JumpToNextCell", "", 0, Array())
N=N+1
Next c
Next l
End sub
Function ePrimo (n as Long) as Boolean
If n = 2 Then
ePrimo = true
Exit Function
End If
If n Mod 2 = 0 Then
ePrimo = false
Else
For d = 3 To Sqr(n) Step 2
If n Mod d = 0 Then
ePrimo = false
Exit Function
End if
Next d
ePrimo = True
End If
End Function
Ver também
[editar | editar código-fonte]- List of prime numbers - diversas listas de números primos, na Wikipédia inglesa.


































































































































































































































































































































































































































































































































































































































































































































































































































































































![{\displaystyle [a]_{m}=\{x\in \mathbb {Z} ;x\equiv a\!\!\!\!{\pmod {m}}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb0baaf8eb33dc005347bcc34bd0980de7f78e33)
![{\displaystyle [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82bc70a8e322f13a3c4e5b9d5d69e8ef097ad8)
![{\displaystyle [a]_{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54d89656467018df3c7644d8776a28eef1b154c5)

![{\displaystyle \mathbb {Z} /_{\equiv \!\!\!\!{\pmod {m}}}=\{[a]_{m};a\in \mathbb {Z} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45299212cbe035716af6931e4b536ae7c8be09f9)




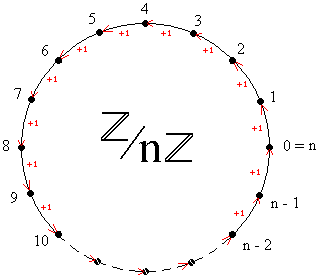
![{\displaystyle [a],[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aacc3bd6224ba6355ffc791ed1f41e25202ced4)
![{\displaystyle [a]+[b]=[a+b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5977b98e7a0ab563b4b4f339caa0ec9dab5b14)
![{\displaystyle [a]\times [b]=[a\times b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59759b3bb57c3982f4d03cd1142272307d0f10c3)
![{\displaystyle [a][b]=[ab]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/709d523ac678f932a75edb3c135db415a516eb13)
![{\displaystyle A=[a]=[a']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3360680eed8a4f7e08d95e79a42816a4543a85bc)
![{\displaystyle B=[b]=[b']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98654edaad6999f6c49cb015dae57378f4ecbdd6)
![{\displaystyle [A]+[B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f2e02bbc65a58189db9d009b692c5ee712807f4)
![{\displaystyle [a+b],[a'+b],[a+b']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b695b22f3265aef2a4741c83745ffa6717c6c1c)
![{\displaystyle [a'+b']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77bf37ca8b5433087b1437509fc5c1de80342e2b)




![{\displaystyle \rho (x)=[x]=[x\!\!\!\!{\pmod {m}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dcf9468bf75be2f36e374095eedef564d637f46)






























































































































