Teoria de números/Congruências

Origem: Wikilivros, livros abertos por um mundo aberto.

Anterior: Equações diofantinas Índice Próximo: Problemas em aberto
Carl Friedrich Gauss
Bendixen - Carl Friedrich Gauß, 1828.jpg

Carl Friedrich Gauss foi um famoso matemático, astrônomo e físico alemão.
Crystal Clear app kaddressbook.png Este livro tem a seguinte tarefa pendente: Incluir breve biografia sobre Carl Friedrich Gauss, enfatizando suas contribuições na teoria de números.

Índice

[editar] Definição

Definição

O inteiro x\,\! é dito congruente ao inteiro y\,\! módulo m\,\!, quando m|x-y\,\!. Neste caso, escreve-se x \equiv y \!\!\!\!\pmod{m}\,\!.

Com essa notação, tem-se para quaisquer inteiros x,y\,\!:

x^2 + y^2 \not \equiv 3\!\!\!\!\pmod{4}\,\!

pois

k \equiv 0\!\!\!\!\pmod{2} \Rightarrow k^2 \equiv 0\!\!\!\!\pmod{4} \,\!

e

k \equiv 1\!\!\!\!\pmod{2} \Rightarrow k^2 \equiv 1\!\!\!\!\pmod{4} \,\!

Como se pode ver na próxima tabela, onde são listadas todas as combinações possíveis para x^2, y^2\,\! e x^2 + y^2\,\! módulo 2\,\!, a soma de dois quadrados nunca é congruente a 3\,\! módulo 4\,\!.

{}_{x^2}\!\!\diagdown\!\!^{y^2} 0 1
0 0 1
1 1 2

Em outras palavras, o simples cálculo feito acima mostra que ao somar dois quadrados perfeitos, o sucessor do resultado nunca é múltiplo de 4\,\!.

Nota
x \equiv y \!\!\!\!\pmod{m} \Leftrightarrow m|x-y\,\! \Leftrightarrow \exists k \in \mathbb{Z}, x-y=mk \Leftrightarrow \exists k \in \mathbb{Z}, x = y + mk \,\!

Sendo assim, a notação para congruências, introduzida por Gauss evita o uso de várias constantes (k, c, m, t, \ldots\,\!) que não são relevantes durante grande parte dos cálculos envolvendo divisibilidade. Atente para a semelhança (visual) entre as seguintes expressões:

x \equiv y \!\!\!\!\pmod{m} \,\!
x = y + mk \,\!
Observação

Conforme o algoritmo da divisão, dados a\in \mathbb{Z}\,\! e m \in \mathbb{Z}^*\,\!existem únicos q,r \in \mathbb{Z}\,\! de modo que:

a = mq + r \,\!, com 0\le r < m\,\!

Isso significa que qualquer inteiro a\,\! é congruente ao seu resto r\,\! na divisão por um inteiro não nulo m\,\!. Uma vez que o resto obtido é único, pode-se definir para cada inteiro m\not = 0\,\! fixado, uma função \rho_m \,\! que a cada número a\in \mathbb{Z}\,\! associa o resto da divisão de a\,\! por m\,\!. A imagem de a\,\! por esta função é denotada por a \!\!\!\!\pmod{m} \,\!. Mais precisamente:

\rho_m: \mathbb{Z} \rightarrow \{0, 1, 2, \ldots ,m-1 \}\,\!
\rho_m (a) = a \!\!\!\!\pmod{m} \,\!

Quando não houver risco de confusão, o índice m\,\! será omitido e será escrito apenas \rho \,\! em vez de \rho_m \,\!.

[editar] A congruência vista como uma relação de equivalência

A partir da noção de congruência módulo um certo inteiro m\,\!, pode-se definir uma relação no conjunto dos números inteiros da seguinte forma:

x \sim y \Leftrightarrow x \equiv y \!\!\!\!\pmod{m}\,\!

Como será mostrado logo a diante, a relação assim definida satisfaz as propriedades de reflexividade, simetria, transitividade, sendo por isso considerada uma relação de equivalência:

  1. \forall x, x \equiv x \!\!\!\!\pmod{m}\,\!
  2. x \equiv y \!\!\!\!\pmod{m} \Rightarrow y \equiv x \!\!\!\!\pmod{m} \,\!
  3. x \equiv y \!\!\!\!\pmod{m} \and y \equiv z \!\!\!\!\pmod{m} \Rightarrow x \equiv z \!\!\!\!\pmod{m} \,\!

De modo geral, é sempre possível construir uma relação de equivalência sobre um conjunto X\,\! a partir de uma função cujo domínio seja X\,\!. De fato, se for definido que:

x \sim y \Leftrightarrow f(x) = f(y)\,\!

então \sim\,\! será uma relação de equivalência em X\,\!, pois \forall x, y \in X\,\!:

  1. f(x) = f(x)\,\!
  2. f(x)=f(y) \Rightarrow f(y)=f(x) \,\!
  3. f(x)=f(y) \and f(y) = f(z) \Rightarrow f(x) = f(z) \,\!

E destas propriedades da igualdade seguem as propriedades correspondentes para a relação \sim\,\!. Em particular, tomando X = \mathbb{Z}\,\!, e f(x) = x \!\!\!\!\pmod{m} \,\!, conclui-se que a congruência é uma relação de equivalência.

[editar] Compatibilidade com as operações

Um fato importante, que não pode deixar de ser mencionado é que a relação de congruência é compatível com as operações do anel dos números inteiros, a saber, a adição e a multiplicação. Uma operação \star\,\!é compatível com uma relação de equivalência \sim\,\! quando a partir de

\left\{\begin{matrix} a & \sim & a'\\ b & \sim & b'\\ \end{matrix}\right.\,\!

pode-se concluir que

a \star b\sim a' \star b'\,\!

No caso da relação de congruência, vê-se que a mesma é compatível tanto com a adição quanto com a multiplicação de números inteiros, como é sintetizado no próximo resultado.

Teorema

Se a, a', b, b'\,\! são números inteiros tais que:

\left\{\begin{matrix} a \equiv a' \!\!\!\!\pmod{m}\\ b \equiv b' \!\!\!\!\pmod{m}\\ \end{matrix}\right.\,\!
então:
\left\{\begin{matrix} a + b \equiv a' + b' \!\!\!\!\pmod{m}\\ a b \equiv a' b' \!\!\!\!\pmod{m}\\ \end{matrix}\right.\,\!

A verificação deste resultado é bem simples, como se pode ver a seguir.

[editar] O anel das classes de congruência

Uma relação de equivalência particiona um conjunto em vários subconjuntos disjuntos, chamadas classes de equivalência.

Sempre que se tem uma relação de equivalência \sim\,\! sobre um conjunto X\,\! é possível definir uma partição P\,\! de tal conjunto. Uma coleção P\,\! de subconjuntos de X\,\! é chamada de partição de X\,\! se todo elemento de X\,\! pertence a exatamente um elemento de P\,\!. Os elementos de P\,\! são disjuntos dois a dois, e sua união é o próprio conjunto X\,\!.

Para definir uma partição de \mathbb{Z}\,\!, usando a congruência módulo m\,\!, primeiramente define-se para cada inteiro a\,\! a classe de equivalência de a\,\!, segundo \sim\,\!, como:

[a]_m = \{ x \in \mathbb{Z}; x \equiv a \!\!\!\!\pmod{m}\}\,\!

Quando o inteiro m\,\! estiver subentendido, será utilizado apenas [a]\,\! para denotar [a]_m\,\!.

Nesses termos, o quociente de \mathbb{Z}\,\! pela relação \equiv \!\!\!\!\pmod{m}\,\! é a partição dada por:

\mathbb{Z}/_{\equiv \!\!\!\!\pmod{m}} = \{[a]_m; a \in \mathbb{Z}\}\,\!

Por simplicidade, denota-se \mathbb{Z}/_{\equiv \!\!\!\!\pmod{m}}\,\! simplesmente como \mathbb{Z}_m\,\!.

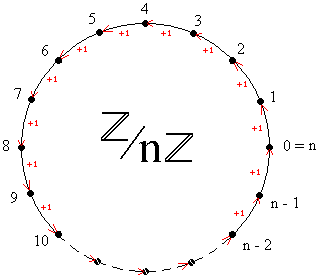
Uma das formas de visualizar essa partição de \mathbb{Z}\,\! é imaginar que sobre um barbante foram marcados todos os números inteiros, separando os números adjacentes sempre por uma mesma distância. Depois disso, para obter uma representação de \mathbb{Z}_m\,\!, enrola-se o barbante em torno de uma circunferência (infinitas vezes!), de modo que o zero ocupe a mesma posição que os inteiros \ldots, -2n, -n, n, 2n, 3n, \ldots\,\!. Você pode então pensar nos elementos de \mathbb{Z}_n\,\! como sendo os n pontos sobre a circunferência que se formou. Veja uma ilustração:

Representação dos inteiros módulo n sobre uma circunferência.

Deste modo, cada ponto da circunferência representa uma das classes de equivalência módulo n\,\!, ou seja, o conjunto dos números inteiros que ficaram sobrepostos naquele ponto da circunferência.


Mas o que há de interessante em particionar o conjunto dos números inteiros?


A grande utilidade de separar os números inteiros em várias classes de congruência é consequência da compatibilidade da congruência com as operações de adição e multiplicação: Sabendo-se que elas são compatíveis, é possível definir em cada \mathbb{Z}_m\,\! novas operações de adição e multiplicação. O procedimento é o seguinte:

Fixado um inteiro m\,\!, e dadas as classes [a], [b]\,\!, define-se:

[a] + [b] = [a + b] \,\!
[a] \times [b] = [a \times b] \,\! (ou simplesmente [a] [b] = [a b] \,\!)

Em outras palavras, a soma (produto) das classes de congruência dos inteiros a, b\,\! é a classe de congruência de sua soma (produto).

É importante notar onde é utilizada a compatibilidade da congruência com as operações de \mathbb{Z}\,\!: Dadas duas classes de equivalência A=[a]=[a']\,\! e B=[b]=[b']\,\!, tanto faz obter [A]+[B]\,\! como sendo [a+b],[a'+b],[a+b']\,\! ou [a'+b']\,\!. Todas essas classes são idênticas!

Mais do que isso, ao definir essas operações, (\mathbb{Z}_m, +, \times)\,\! torna-se um anel com unidade, ou seja, são válidas as seguintes propriedades:

Além disso, tem-se um homomorfismo de anéis entre \mathbb{Z} = \{ 0, \pm 1, \pm 2, \pm 3, \ldots \}\,\! e \mathbb{Z}_m = \{ m\mathbb{Z} + 0, m\mathbb{Z} + 1,\ldots , m\mathbb{Z} + (m-1) \} \,\!:

\rho: \mathbb{Z} \rightarrow \mathbb{Z}_m \,\!
\rho(x) = [x] = [x \!\!\!\!\pmod{m}]\,\!


Recordando...
Um anel com unidade é um conjunto R equipado com duas operações binárias + : R × R ? R e · : R × R ? R (onde × denota o produto cartesiano), chamadas de adição e multiplicação, tais que:
  • (R, +) é um grupo abeliano com elemento identidade, isto é, para todo a, b, c em R, vale o seguinte:
    • (a + b) + c = a + (b + c) (+ é associativa)
    • 0 + a = a (0 é a identidade)
    • a + b = b + a (+ é comutativa)
    • para cada a em R existe −a em R tal que a + (−a) = (−a) + a = 0 (−a é o elemento inverso de a)
  • (R, ·) é um monóide com elemento identidade 1, isto é, para todo a, b, c em R, vale:
    • (a · b) · c = a · (b · c) (· é associativa)
    • 1 · a = a · 1 = a (1 é a identidade)
  • Multiplicação se distribui em relação a adição:
    • a · (b + c) = (a · b) + (a · c)
    • (a + b) · c = (a · c) + (b · c).

[editar] Exemplos

As próximas tabelas são as tabuadas das operações de adição e multiplicação no anel \mathbb{Z}_6\,\!. Note que este é um número composto, e que (por esse motivo) existem elementos não nulos em \mathbb{Z}_6\,\! cujo produto é zero (no caso, 2\times 3 = 3\times 4 = 0\,\!).

+\,\! 0 1 2 3 4 5
0 0 1 2 3 4 5
1 1 2 3 4 5 0
2 2 3 4 5 0 1
3 3 4 5 0 1 2
4 4 5 0 1 2 3
5 5 0 1 2 3 4
\times\,\! 0 1 2 3 4 5
0 0 0 0 0 0 0
1 0 1 2 3 4 5
2 0 2 4 0 2 4
3 0 3 0 3 0 3
4 0 4 2 0 4 2
5 0 5 4 3 2 1

Outro fato curioso que pode ser identificado em alguns anéis é a presença de elementos nilpotentes, ou seja, tais que alguma de suas potências é nula. Por exemplo, em \mathbb{Z}_{12}\,\!, tem-se 6^2 = 0\,\!.

Veja a tábua de multiplicação completa para o anel de inteiros módulo 12\,\!:

\times\,\! 0 1 2 3 4 5 6 7 8 9 10 11
0 0 0 0 0 0 0 0 0 0 0 0 0
1 0 1 2 3 4 5 6 7 8 9 10 11
2 0 2 4 6 8 10 0 2 4 6 8 10
3 0 3 6 9 0 3 6 9 0 3 6 9
4 0 4 8 0 4 8 0 4 8 0 4 8
5 0 5 10 3 8 1 6 11 4 9 2 7
6 0 6 0 6 0 6 0 6 0 6 0 6
7 0 7 2 9 4 11 6 1 8 3 10 5
8 0 8 4 0 8 4 0 8 4 0 8 4
9 0 9 6 3 0 9 6 3 0 9 6 3
10 0 10 8 6 4 2 0 10 8 6 4 2
11 0 11 10 9 8 7 6 5 4 3 2 1

O próximo passo é tentar compreender algebricamente os conjuntos ( \mathbb{Z}_{m} , + ) \,\!.


Crystal Clear app kaddressbook.png Este livro tem a seguinte tarefa pendente: Revisar/reescrever/excluir o trecho a seguir (até onde diz "Corolário da p7").

No próximo diagrama pode ser observada a estrutura aditiva de ( \mathbb{Z}_{m} , + ) \,\!:

\rho: \mathbb{Z} \rightarrow \mathbb{Z}_m\,\!
G \ \ \ H\,\!
mZ \rightarrow 0\,\!

H\,\! é subgrupo aditivo de \mathbb{Z}_m \,\!.

H = \rho (G)\,\!, G\,\! subgrupo aditivo de \mathbb{Z}_m \,\!

mZ = ker (\rho) \subset G \,\!
G = d \mathbb{Z}\,\!
m \mathbb{Z} \subset d \mathbb{Z} \Leftrightarrow d|m\,\!. Logo H = d \mathbb{Z} / m \mathbb{Z} \,\!
\overline{x} \in \mathbb{Z}_m\,\!
ord^+_m(x) = k \,\!
\overline{k \cdot x} = k \cdot \overline{x} = \overline{0}\,\!
kx \equiv 0 \!\!\!\!\pmod{m} \,\!

Menor k \,\! tal que m | kx \,\!. kx = mmc (x,m) = \frac{x \cdot m}{(x,m)}\,\!

ord^+_m(x) = \frac{m}{(x,m)}\,\!
(x,m) = 1 \Rightarrow \overline{x}\,\! gera \mathbb{Z}_m \,\!, ou seja são os blocos básicos.

Observe a seguinte tabela, onde constam as ordens aditivas módulo 6.

+\,\! 1 2 3 4 5 6
0 0
1 1 2 3 4 5 0
2 2 4 0
3 3 0
4 4 2 0
5 5 4 3 2 1 0
G = d \mathbb{Z}\,\!
m \mathbb{Z} \subset d \mathbb{Z} \Leftrightarrow d|m\,\!. Logo H = d \mathbb{Z} / m \mathbb{Z} \,\!


Corolário da p7

Se p é primo então \mathbb{Z}_p \,\! não tem subgrupos triviais.
xy \equiv 0 \!\!\!\!\pmod{p} \,\!
p|xy \Rightarrow p|x\,\! ou p|y\,\!. Isso implica que x = \overline{0}\,\! ou y = \overline{0}\,\!, donde \mathbb{Z}_p\,\! é domínio de integridade e portanto, \mathbb{Z}_p\,\! é corpo (todo domínio finito é corpo).

Exemplo:

\times\,\! 0 1 2 3 4
0 0 0 0 0 0
1 0 1 2 3 4
2 0 2 4 1 3
3 0 3 1 4 2
4 0 4 3 2 1

Outra consequencia é que, fixado z não nulo em Z_p, a função \mu: \mathbb{Z}_p \rightarrow \mathbb{Z}_p\,\!, definida por \mu (x) = z x\,\! é injetiva, pois se \mu (x) = \mu (x') \,\!, ou seja, z x \equiv z x' \!\!\!\!\pmod{p} \,\!, então z (x -x') \equiv 0 \!\!\!\!\pmod{p} \,\!. Como (z,p) = 1\,\!, pode-se concluir que x -x' \equiv 0 \!\!\!\!\pmod{p} \,\!, ou seja, x \equiv x' \!\!\!\!\pmod{p} \,\!.

Em particular, da sobrejetividade de \mu\,\!, e de 1 \in \mathbb{Z}_p \,\! (a imagem de \mu\,\!), segue a existência de z' \in \mathbb{Z}_p \,\! tal que \mu (z') = 1\,\!, ou seja, tal que z z' \equiv 1 \!\!\!\!\pmod{p} \,\!.

Algebricamente, o significado da sobrejetividade de \mu\,\! é a existência de um elemento inverso para cada z \in \mathbb{Z}_p\,\! (quando p é primo). No entanto, a argumentação anterior é não construtiva, pois não indica um método para obter o inverso de um certo z \in \mathbb{Z}_p\,\!.

Pode-se obter outra justificativa para a existência de elementos inversos em \mathbb{Z}_p\,\! usando o teorema de Bezout. De fato, \bar{z} \not = \bar{0}\,\! se, e somente se, p \not | z\,\!, ou seja, se, e somente, (p,z) = 1\,\!. Usando o algoritmo de Euclides, pode-se então encontrar u,v \in \mathbb{Z}\,\! tais que pu+zv=1\,\!. Em particular, usando congruências módulo p segue pu+zv\equiv 1 \!\!\!\!\pmod{p} \,\!. Donde 0+zv\equiv 1 \!\!\!\!\pmod{p} \,\!, ou seja, zv\equiv 1 \!\!\!\!\pmod{p} \,\!. Portanto, o z'\,\! procurado é simplesmente v \!\!\!\!\pmod{p} \,\!.

[editar] Resumindo

Os fatos mais relevantes apresentados na discussão feita até agora podem ser sintetizados da seguinte forma:

  • Para qualquer m \in \mathbb{Z}\,\!, tem-se um anel finito \mathbb{Z}_m\,\!;
  • São equivalentes:
    • \mathbb{Z}_m\,\! é corpo;
    • \mathbb{Z}_m\,\! é um domínio;
    • m\,\! é um número primo;
(propriedades algébricas dos conjuntos \mathbb{Z}_m\,\! -- anéis regulares --correspondem a propriedades aritméticas dos numeros inteiros m\,\!).
  • São também equivalentes:
    • \mathbb{Z}_m\,\! tem divisores de zero;
    • m\,\! é um número composto;

[editar] Unidades

Para um inteiro m\,\! arbitrário (seja ele primo ou não), podem ser considerada a questão:

Quais elementos de \mathbb{Z}_m\,\! são inversíveis?

Antes de responder essa pergunta, convém introduzir uma notação específica para denotar o conjunto dos elementos u \in \mathbb{Z}_m\,\! que possuem inverso multiplicativo:

Definição

Um elemento de \mathbb{Z}_m\,\! é chamado de unidade quando possui inverso multiplicativo. O conjunto das unidades de \mathbb{Z}_m\,\! denota-se por U_m\,\!.

[editar] Exemplos

  • Se p é número primo, então U_m = \mathbb{Z}_m / \{ 0 \} = \{ \bar{1}, \bar{2}, \ldots , \overline{p-1} \} \,\!
  • U_6 = \{ \bar{1}, \bar{5} \} = \{ \pm \bar{1}\} \,\!
  • U_7 = \{ \bar{1}, \bar{2}, \bar{3}, \bar{4}, \bar{5}, \bar{6}, \bar{7} \}\,\!

[editar] Propriedades das unidades

Pode-se verificar que para qualquer m\,\!, o conjunto U_m\,\!, das unidades de \mathbb{Z}_m\,\!, é um grupo multiplicativo finito. Em particular, sempre que u,v \in U_m\,\!, tem-se uv \in U_m\,\!. Além disso, 1 \in U_m\,\! e existe v \in U_m\,\! tal que uv = 1 \,\!.

Novamente, a estrutura de U_m\,\! reflete as propriedades aritméticas de m\,\!. Para melhor entender o que isso significa, é interessante saber para cada m\,\! a quantidade de elementos de U_m\,\!. É razoável esperar que esse número varie com m\,\!, então o melhor é definir uma função que associa m\,\! com a cardinalidade de U_m\,\!:

Definição

A função U_m\,\! de Euler é a função que associa a cada m\,\! o número de elementos de U_m\,\!:

\phi (m ) = | U_m | \,\!
Observações
  • Convenciona-se que \phi (1) = 1\,\!.
  • O valor \phi (m)\,\! é justamente a quantidade de números de 1\,\! a m\,\! que são coprimos com m\,\!:

[editar] Exemplos

  • Quando p\,\! é um número primo, tem-se \phi (p) = p-1\,\!.
  • Por outro lado, para números compostos, \phi (m)\,\! pode ser bem menor do que m-1\,\!. Em particular, \phi (6) = | U_6 | = | \{ \pm \bar{1}\} | = 2 < 5-1 = 4\,\!.

[editar] Curiosidades

O valor de \phi (m)\,\! é justamente a quantidade de frações próprias não negativas com denominador m\,\! (ou seja, \frac{0}{m}, \frac{1}{m} , \ldots, \frac{m-1}{m}\,\!) que já estão na forma irredutível.

[editar] Exemplo

No caso m = 6\,\! apresentado anteriormente, temos as seguintes frações próprias com tal denominador:

\frac{0}{6}, \mathbf{\frac{1}{6}}, \frac{2}{6}, \frac{3}{6}, \frac{4}{6}, \mathbf{\frac{5}{6}}\,\!

Escrevendo cada uma delas na forma irredutível obtém-se:

\frac{0}{1}, \mathbf{\frac{1}{6}}, \frac{1}{3}, \frac{1}{2}, \frac{2}{3}, \mathbf{\frac{5}{6}}\,\!

Pode-se então conferir que, como era esperado, só duas das frações já estavam em sua forma irredutível: \frac{1}{6}\,\! e \frac{5}{6}\,\!.

Note que ao escrever cada fração em sua forma irredutível os denominadores que surgem são todos divisores de m = 6\,\!. Além disso, tem-se:

  • 1 fração com denominador 1
  • 1 fração com denominador 2
  • 2 fração com denominador 3
  • 2 fração com denominador 6

Totalizando 1+ 1 + 2 + 2 = 6\,\! frações. Por outro lado, a seguinte tabela indica um fato muito interessante:

d Número de frações com denominador d \phi (d)\,\!
1 1 1
2 1 1
3 2 2
6 2 2

Percebe-se que as duas últimas colunas coincidem. Mas o que isso significa?

Isso quer dizer que o número m = 6\,\! é, na verdade, igual a soma dos valores \phi (d)\,\! de cada um dos divisores d\,\!. Em símbolos:

6 = 1+ 1 + 2 + 2 = \phi (1) + \phi (2) + \phi (3) + \phi (6)\,\!

Pode-se verificar que essas duas propriedades são válidas em geral:

  • \phi (m)\,\! é igual à quantidade de frações próprias não negativas com denominador que estão na forma irredutível.
  • m = \sum_{d|m} {\phi (d)} \,\!

[editar] Equações lineares

Uma questão muito natural é investigar em que casos há alguma solução para equações lineares do tipo

ax \equiv y \!\!\!\!\pmod{m}\,\!

[editar] Exemplo de equação linear com apenas uma solução

Considere em \mathbb{Z}_8\,\! a seguinte equação:

3x = 2 \,\!

ou, em termos de congruências,

3x \equiv 2 \!\!\!\!\pmod{8}\,\!

Sabendo que mdc(3,8)=1\,\!, é possível determinar r,s\,\! tais que

3r+8s=1\,\!

Por exemplo, pode-se tomar r=-5\,\! e s=2\,\!. Outra possibilidade é r=3\,\! e s=-1\,\!. Neste caso, nota-se que:

3\cdot 3 + 8\cdot (-1) \equiv 1 \!\!\!\!\pmod{8}\,\!

ou seja,

3\cdot 3 + 0 \equiv 1 \!\!\!\!\pmod{8}\,\!

significando que 3 = 3^{-1}\,\! em \mathbb{Z}_8\,\!, ou seja, que neste anel o inverso multiplicativo de 3\,\! é ele mesmo. Sabendo disso, é possível resolver

3x \equiv 2 \!\!\!\!\pmod{8}\,\!

de forma análoga à utilizada em \mathbb{Z}\,\!: Multiplicando-se ambos os membros pelo inverso de 3\,\!, segue:

3\cdot 3x \equiv 3\cdot 2 \!\!\!\!\pmod{8}\,\!

ou seja,

1 \cdot x \equiv 6 \!\!\!\!\pmod{8}\,\!

Conclui-se então que, nesse exemplo, há uma somente uma solução em \mathbb{Z}_8\,\! para a equação dada. Observe ainda que o número y=2\,\! não teve qualquer influência no número de soluções para o problema. Isso pode ser percebido considerando para cada x\in\mathbb{Z}_8\,\! o resultado de sua multiplicação por a=3\,\!:

0 1 2 3 4 5 6 7
\times 3\,\! 0 3 6 1 4 7 2 5

Note que se tem uma permutação dos elementos de \mathbb{Z}_8\,\! e que, portanto, o único elemento que é levado em 2\,\! ao ser multiplicado por 3\,\! é o 6\,\!. Essa unicidade permaneceria se o 2\,\! fosse trocado por qualquer outro elemento.

[editar] Exemplo de equação linear sem solução

Considere a seguinte equação em \mathbb{Z}_8\,\!:

4x = 5\,\!

que em termos de congruências se escreve como

4x \equiv 5 \!\!\!\!\pmod{8}\,\!

Já foi mostrado que ela é equivalente à seguinte equação em \mathbb{Z}\,\!:

4x = 5 + 8k\,\!

ou seja,

4(x - 2k) = 5\,\!

É claro que tal equação não adimite sequer uma solução inteira, uma vez que à esquerda tem-se um número par e a direita um ímpar, ou para ser mais exato, pois 4 = mdc(4,8) \not | 5\,\!.

[editar] Exemplo de equação linear com duas soluções

Como um último exemplo antes de conhecer o teorema que dá uma resposta definitiva sobre o número de soluções de uma equação linear em \mathbb{Z}_m\,\!, considere em \mathbb{Z}_8\,\! a equação:

2x = 6\,\!

ou seja,

2x \equiv 6 \!\!\!\!\pmod{8}\,\!

O problema de encontrar soluções para esta equação é equivalente a encontrar inteiros x, y\,\! tais que:

2x = 6 + 8y\,\!

Dividindo ambos os membros por dois, obtem-se

\frac{2}{2}x = \frac{6}{2} + \frac{8}{2}y \,\!

ou seja,

x = 3 + 4y \,\!

Em termos de congruências, segue:

x \equiv 3 \!\!\!\!\pmod{4}\,\!

Os números inteiros que verificam essa congruência são os termos da progressão aritmética:

\{ \ldots, -5, -1, 3, 7, 11, 15, 19, \ldots \}\,\!

No entanto, como as soluções são buscadas em \mathbb{Z}_8\,\!, devemos considerar os números acima módulo 8\,\!:

\{ \ldots, 3, 7, 3, 7, 3, 7, 3, \ldots \}\,\!

ou seja, o conjunto das soluções é:

S = \{ 3, 7 \}\,\!


Em suma, verificou-se através dos exemplos anteriores que é possível encontrar em \mathbb{Z}_8\,\! equações do tipo ax=y\,\! que possuam uma ou duas soluções, e mesmo equações que não adimitem solução. Essa é uma notavel diferença entre corpos (como \mathbb{R}\,\!, \mathbb{Q}\,\! e \mathbb{Z}_p\,\!) e anéis. Por exemplo, em \mathbb{Q}\,\! ou \mathbb{R}\,\! você deve estar habituado a resolver ax=y\,\!, simplesmente dividindo os dois membros por a\,\! (e talvez descrevendo esse procedimento como "passar o a\,\! para o lado direito, dividindo..."). No entanto, é tempo de notar que isso só é possível quando a\,\! possui inverso. Em \mathbb{Q}\,\!, todo número não nulo possui inverso. Mas isso não é verdade em todo anel! Por essa razão torna-se necessário tomar algum cuidado ao resolver equações nos aneis \mathbb{Z}_m\,\!. Fique atento!


[editar] Exercícios

  1. Mostre que, se x \equiv y \!\!\!\!\pmod{m}\,\! e f\,\! é um polinômio com coeficientes inteiros, então f(x)\equiv f(y)\!\!\!\!\pmod{m}\,\!.
  2. Que propriedade aritmética do número inteiro m\,\! corresponde a existência de elementos nilpotentes em \mathbb{Z}_m\,\!? (Lembre-se, um elemento é nilpotente quando alguma de suas potências inteiras é igual a zero)
Obtido em "http://pt.wikibooks.org/wiki/Teoria_de_n%C3%BAmeros/Congru%C3%AAncias"
Outras línguas