Cálculo (Volume 1)/Imprimir
| Cálculo (Volume 1) Para as disciplinas Cálculo I e II | ||||

| ||||
Este livro é resultado do conhecimento, do empenho e da dedicação de várias pessoas, que acreditam que o conhecimento deve ser de todos os que aspiram obtê-lo, sendo a doação um ato que é recompensado pela satisfação em difundir o saber.
Dentre os editores que participaram da criação deste livro, damos crédito pelas seguintes competências:
- Ajustes de formatação
- Categorização
- Conteúdo
- Correções
- Proteção do conteúdo
Prefácio
[editar | editar código-fonte]Todos aprendemos, até este ponto, a matemática elementar, com ela podemos lidar com inúmeras de nossas necessidades mais corriqueiras do dia a dia. A partir de agora, teremos a oportunidade de dispor de recursos mais sofisticados.
O Cálculo, em conjunto com outras disciplinas, faz parte do aprendizado da matemática de nível superior. Ele é uma valorosa ferramenta de análise, muito utilizada em ciências exatas. Esta ferramenta recebeu o nome cálculo, como forma abreviada da expressão "Cálculo Infinitesimal" ou "Cálculo Diferencial e Integral". Este livro explora a parte inicial do estudo de cálculo básico, presente nos cursos de nível superior mais voltados às ciências exatas e suas ramificações. Por ter um caráter introdutório, permite ao estudante fazer gradativamente uma transição do pensamento de nível médio para nível universitário. Com ele iremos navegar pelas análises algébricas, numéricas e geométricas, lidando com valores tão pequenos que podem ser considerados relativamente ínfimos. Ao mesmo tempo, iniciaremos as análises de quantidades, desses elementos infinitesimais, tão numerosas que poderíamos chamá-las de populações gigantescas.
Este livro utiliza as notações e as siglas mais encontradas nos livros didáticos de Cálculo no Brasil, algumas notações comuns em livros "on-line" seguem o padrão norte-americano e por isso estão fora dos objetivos desta publicação, que foi idealizada para ser instrumento de aprendizado para nativos da língua portuguesa, alguns exemplos de notações são encontradas principalmente nas funções trigonométricas, como o seno que simbolizamos enquanto que em outros livros verificamos , ou tangente que notamos enquanto que em outros vemos .
Dividimos o estudo de Cálculo em 3 (três) livros, que não são necessariamente indicados especificamente para as subdivisões do estudo feito nas universidades, embora tenhamos alguns cursos onde há uma divisão da disciplina em até 6 (seis) módulos. Para aproximar a seqüência dos tópicos à dos cursos mais conceituados, fizemos uma pesquisa e adequamos os índices ao cronograma destes cursos, para isso pesquisamos universidades públicas e privadas no Brasil, obviamente, seria impossível adequar a seqüência dos tópicos para todos os cursos que se utilizam deste estudo, acredito que está próxima da média de adequação.
Para sequenciar os capítulos e indicar a sua aplicação foi incluída uma tarja cinza no topo de cada página dos livros desta série, que tem o objetivo de orientar a que nível de dificuldade se destina o conteúdo, o cronograma adotado é o mais completo, portanto, algumas partes dos livros podem ser retiradas do currículo do curso, conforme a instrução do tutor ou mestre que o formulou.
Espero que todos nós, autores e leitores, tenhamos um bom aproveitamento advindo do desenvolvimento ou do estudo do conteúdo deste e dos outros livros sobre este tema.
A seguir será apresentada uma relação dos símbolos utilizados neste wikilivro de cálculo, juntamente com os links para os módulos que abordam o seu uso. Utilize este módulo sempre que precisar fazer uma consulta rápida.
- Assíntota
- Derivada
- aplicações, 1
- de funções implicitas
- Diferencial
- Domínio
- Função
- bijetiva
- contínua
- implícita
- injetiva
- inversa
- sobrejetiva
- Infinitesimal
- Infinito
- Integração
- funções racionais
- funções trigonométricas
- imediata
- por
- mudança de variáveis
- partes
- substituição trigonométrica
- Integral
- aplicações
- áreas
- médias
- imprópria
- indefinida
- de Riemann
- Intervalos
- abertos e fechados
- de crescimento e decrescimento
- Limite
- de funções
- lateral
- infinito
- Máximos e mínimos
- Primitiva
- Ponto
- crítico
- de inflexão
- de máximo
- de mínimo
- Regra de L'Hopital
- Reta
- tangente
- Somas de Riemann
- Tangente a uma curva
- Taylor
- polinômio
- resto
- Teorema
- da
- função implícita
- funçõ inversa
- de
- Bolzano-Weierstrass
- Rolle, 1
- Taylor
- do
- valor médio para derivadas, 1
- valor intermediário
- fundamental do cálculo
- Valor
- absoluto
- médio
- Velocidade
Conceitos básicos
[editar | editar código-fonte]Definições iniciais:
[editar | editar código-fonte]Para uma melhor compreensão do conteúdo subseqüente, sugerimos observar o tópico: Funções, no livro: Matemática elementar, pois o estudo completo de funções foge do escopo deste livro. Neste capítulo iremos destacar princípios e notações que nos serão úteis ao longo deste livro.
Função, domínio e imagem
[editar | editar código-fonte]Seja um conjunto de pontos A, cujos membros são os números em , então tomamos e denominamo-la variável independente, visto que, arbitrariamente, lhe podemos atribuir qualquer valor em e portanto dizemos que:
A é o domínio da variável .
Da mesma forma, admitamos um conjunto de pontos B, cujos membros são números que são obtidos única e exclusivamente por um conjunto de regras matemáticas , quando números arbitrários em A lhe são transferidos; visto que há um único valor assumido para cada valor arbitrário transferido a , dizemos que:
B é função de A.
Sendo B obtido através das regras de :
A é domínio da função .
Da mesma forma, como B é restrito aos valores definidos por A e às regras definidas por , os seus elementos espelham estas condições, portanto, podemos dizer que:
B é imagem da função .
Extensões de domínios
[editar | editar código-fonte]Observemos a expressão: Note que assim que atribuirmos valores a , a mesma assumirá valores inválidos, valores de raízes quadradas de números negativos, para sanar este problema, poderemos atribuir uma faixa de valores válidos para o domínio de , então teremos:
Assim, teremos um domínio restrito a valores iguais ou menores que 12, portanto, incluindo-o, este extremo ao qual pertence o valor 12 chamamos de extremo fechado.
Temos uma situação semelhante, porém com uma sutil diferença, quando temos que fazer: , neste caso, temos que restringir o valor 0 e todos os números abaixo dele, desta forma:
Poderemos atribuir apenas valores maiores que 0, uma vez que este valor não pertence ao conjunto de números que podem ser atribuídos à variável, chamamos este de extremo aberto.
Notações
[editar | editar código-fonte]O conjunto de números B dos quais dependem do conjunto A de onde temos , estabelecemos o par de números , ou simplesmente:
Este é chamado de par ordenado.
Sendo também a representação dos valores de , então podemos dizer que:
Sendo o valor de quando definido pelas operações em .
Faixas de valores que delimitam os domínios podem ser representados com desigualdades, como nos exemplos abaixo:
Porém, os extremos podem ser colocados em um par entre delimitadores de forma que, para os extremos fechados usamos os delimitadores [ ou ], para os extremos abertos usamos ( ou ), habilitando-nos a identificar os extremos mais claramente, desta forma podemos identificar os domínios do exemplo acima desta forma:
Também é comum usar colchetes invertidos para extremos abertos:
Operações com funções
[editar | editar código-fonte]Consideremos duas funções f e g; admitindo que as duas são, intuitivamente, expressões que se traduzem em valores, podemos dizer que:
Sendo D(f) o domínio da função f e D(g) o domínio da função g, o domínio da função resultante das operações acima é sempre:
Limites
[editar | editar código-fonte]Breve explanação
[editar | editar código-fonte]Vejamos o gráfico a seguir:
Figura 1
O gráfico representa a função definida pela regra:
Esta função não está definida para , pois não faz sentido escrever . No entanto, podemos calcular para valores de muito próximos de 6. Observe a tabela:
| 5,5 | 5,8 | 5,99 | 6 | 6,05 | 6,2 | 6,5 | |
| 0,75 | 0,9 | 0,995 | 1,025 | 1,1 | 1,25 |
Se fizermos temos ; se agora fizermos teremos ; depois fazendo teremos ; portanto quando nós aproximamos de 6, vemos que também aproximamos de 1. Intuitivamente faremos o mesmo usando valores maiores que 6: se tivermos teremos ; e para teremos ; finalmente, se teremos e vemos que o mesmo acontece[1].
O que isto quer dizer?
Acontece que, quando aproximamos de 6, se aproxima de 1, o que indica uma tendência de se igualar a 1. Perceba que quando se aproxima de 6, de forma a alcançar o limite entre ele e o número mais próximo a ele, inevitavelmente faz com que também alcance um número ainda mais próximo de 1. Então dizemos que: se então, o limite de quando tende a 6 é igual a 1.
Como veremos mais adiante, isto é representado pela seguinte notação:
Como pode ver, acabamos de caracterizar o conceito de limite a partir da noção intuitiva de aproximar um número de outro.
Mas como podemos dizer "se aproximar" em termos matemáticos?
Se levarmos em consideração que ao aproximar duas coisas, a distância entre elas diminui, fica fácil perceber que será necessário medir a distância entre os números. Sendo assim, vale a pena recordar que a distância entre dois números reais é dada pela fórmula . Assim, usando essa fórmula podemos dizer que, por exemplo:
- Se é um número pequeno e então está próximo de ;
- Se diminuimos gradativamente o valor de , e ao mesmo tempo escolhemos satisfazendo , podemos dizer que estamos aproximando de L;
Com isso em mente, vamos retomar o nosso exemplo. A dependência entre a variação de e a variação dos valores assumidos pela função pode agora ser expressa de uma forma bem simples. Como é mostrado na tabela, é possível fazer ficar extremamente próximo de 1, bastando escolher valores de suficientemente próximos de 6. Assim, se queremos fazer ficar menor que , é suficiente encontrar um valor de pequeno o bastante e fazer escolhas de que satisfaçam , ou seja, basta escolher próximo de 6.
Analisando as condições
[editar | editar código-fonte]| Sugestão de aprimoramento: Remover esta seção "Analisando as condições", conforme este tópico da discussão |
Seja a função , onde . Façamos isto apenas para restringir o escopo da análise a funções mais simples e assim, que isto permita-nos colocar as condições dentro de parâmetros mais fáceis de analisar.
Sendo , definido ou não em um determinado ponto do domínio, verificamos a existência de valores que tendem a se aproximar de um valor , próximo aos valores trivialmente encontrados para a função em pontos próximos e com valores conhecidos. Então, arbitramos um número , delimitando uma região em de forma que as condições sejam suficientes para garantir que:
Ao tomarmos um subintervalo em com extensão , o efeito esperado é que tenhamos delimitado um valor correspondente para . Consideramos que temos um número , neste intervalo, para todo que obtemos quando arbitramos um na função. Da mesma forma que temos um esperado valor em devemos ter um número no domínio, tal que:
Devemos ter o cuidado de observar que a afirmativa acima exige que o valor da diferença não seja nulo, caso contrário a relação de correspondência dos valores na função e no domínio não existiria.
Caso as condições acima sejam satisfeitas e a relação entre os valores seja possível, dizemos que é o limite de quando tende a .
Definição
[editar | editar código-fonte]Adotamos a notação
para dizer que a função possui a seguinte propriedade:
De agora em diante, para indicar que uma função tem esta propriedade, usaremos indiferentemente qualquer das seguintes alternativas:
- é o limite de , quando tende para , ou que
- tende quando tende para
ou com símbolos:
- quando
Observação
Para aqueles que também se interessam por lógica e fundamentos da matemática, podemos reescrever a definição anterior usando as notações do cálculo quantificacional clássico. Assim, dado , diremos que , quando:
Interpretação intuitiva da definição
[editar | editar código-fonte]Uma forma de compreender, de forma intuitiva, esta definição, é ver o limite como um jogo. Neste jogo, exite um proponente e um desafiante. O proponente declara que
Então cabe, ao desafiante, propor um número . Sempre que o desafiante propuser algum , o proponente deve exibir um e provar que, sempre que , necessariamente temos que
Como exemplo, digamos que a função seja f(x) = x + 1, e o proponente declara que
(uma proposição claramente absurda). Então, caso o desafiante proponha , basta ao proponente escolher , porque para valores de x entre -1/2 e 1/2, temos que f(x) está entre 1/2 e 3/2, ou seja, a distância de f(x) para 2 é menor que 10. Só que isto não é o bastante, o proponente deve responder ao desafio para todo , então caso o desafiante proponha , o proponente não será capaz de encontrar um com a propriedade desejada.
Propriedades
[editar | editar código-fonte]Uma vez motivada a definição do conceito de limite, e apresentada sua caracterização formalmente, é muito útil garantir que os limites satisfazem certas propriedades operatórias, no sentido de que pode-se fazer operações com as expressões que representam limites. As principais propriedades válidas para limites são apresentadas nos teoremas T1 até T6.
Resumidamente, T1 garante que o limite de uma função em um ponto (ou no infinito) é único. Isso significa que quando duas pessoas se propõe a calcular um limite (que exista), elas chegarão obrigatoriamente a um mesmo resultado. Isso justifica por exemplo o uso da expressão o limite de f(x) no ponto a em vez de um limite de f(x) no ponto a.
O teorema T2 estabelece a somatividade dos limites: para somar dois limites que existem, podemos somar as duas funções e calcular apenas o limite desta soma. Uma propriedade análoga vale para a diferença entre limites.
Os teoremas seguintes (de T3 até T6) exploram o mesmo tipo de propriedade para as operações de multiplicação, divisão, potenciação e radiciação de limites. Observe que tradicionalmente estas operações são definidas para números reais. No entanto, talvez por causa de sua simplicidade, podem ser facilmente estendidas para operações entre funções.
Considere, por exemplo, o caso da potenciação. O teorema T5, mostra que para se calcular o limite da (função) n-ésima potência de f(x) que tem limite no ponto a, é suficiente calcular a n-ésima potência do (número dado pelo) limite de f(x) no ponto a.
T1 - (Unicidade)
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja uma função real se o limite da mesma em um ponto existe, então ele é único. Em outras palavras: | ||
| Se e então |
Demonstração:
Proponhamos que e , mas .
Logo, pela definição de limite, teremos que admitir que para cada , existe tal que:
para todo que satisfaz
Além disso, existe para o qual vale
sempre que verifica a desigualdade
Como e não são iguais, a diferença é não nula.
Da desigualdade triangular:
Se tivermos um e , serão válidas as condições:
Teremos em consequência que:
para todo para o qual .
Como podemos arbitrar , teremos, ao fazer , que:
Mas isto é contraditório, portanto .
T2 - (Soma e diferença)
[editar | editar código-fonte]
| ||
|---|---|---|
| Sejam duas funções e , cujo limite em um ponto exista. O limite da soma (ou da diferença) das funções no ponto existe e é: | ||
Demonstração:
Faremos a demonstração apenas para o caso da soma de funções, deixando a cargo do leitor verificar que a propriedade análoga para a diferença de funções pode ser provada de forma parecida.
Tomando e , devemos, pela definição, provar que:
Dado qualquer positivo, existe algum positivo, para o qual sempre que satisfaz
Posto que existem os limites de e em , já sabemos que para quaisquer e positivos, existem e positivos satisfazendo:
- , tal que
- , tal que
e pela desigualdade triangular:
Então, ao arbitrar , existe , de modo que se vale:
, ou seja,
Observação
[editar | editar código-fonte]Ao provar a propriedade para a diferença de funções, a principal mudança é no passo onde é utilizada a desigualdade triangular. Em tal caso, deveriamos observar que:
T3 - (Produto)
[editar | editar código-fonte]
| ||
|---|---|---|
| Se existem os limites das funções e em um ponto , então o limite do produto das funções neste ponto existe, e é dado por: | ||
Demonstração:
Consideremos que e que .
Queremos verificar se para cada positivo, existe algum positivo, tal que
, para todo que verifica
Considerando que existem os limites e , é possível encontrar certo , para o qual
- (1) sempre que e .
do que podemos concluir que, para estes valores de , vale .
Mas para qualquer , com e , também existem valores positivos e , de modo que
- (2), quando e e
- (3), se e .
Então, se , e , valem as desigualdades (1), (2) e (3).
Vamos então trabalhar com a expressão para concluir que ela é fica menor que para estes valores de . Primeiramente, observe que
Usando a desigualdade triangular nesta última expressão, e observando que , obtemos
Aplicando as desigualdades (1), (2) e (3), resulta
Como , concluimos que
Portanto, , o que confirma a validade do teorema.
T4 - (Razão)
[editar | editar código-fonte]
| ||
|---|---|---|
| Se existem os limites das funções e em um ponto , e se o limite da função no ponto é diferente de zero, então o limite da razão das funções neste ponto existe e é: | ||
Demonstração:
Seja . Basta mostrar que , e aplicar a regra do produto para .
Queremos verificar se para cada positivo, existe algum positivo, tal que
, para todo que verifica
Mas esta expressão pode ser reescrita como: .
A ideia agora é mostrar que, na fração acima, temos que o denominador é um número não muito pequeno, enquanto que o numerador é um número pequeno.
Como g(x) se aproxima de M, vamos forçar o denominador a ser um número maior (em módulo) que , e vamos, portanto, forçar o numerador a ser um número menor (em módulo) que . Assim, a razão dos dois será menor (em módulo) que .
- Denominador
Pelo fato de , temos que para o número positivo existe um tal que .
Mas isto implica, em particular, que .
Portanto, temos que .
- Numerador
É imediato, pela propriedade da subtração de limites, que, como , temos que existe tal que .
- Fração
Agora basta tomar , e observar o resultado desejado.
T5 - (Potência)
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função , o limite da função em um ponto , quando a mesma é elevada a um expoente inteiro , é: | ||
Demonstração:
De fato, para cada número natural temos:
O que, pelo teorema do produto, é igual ao produto dos limites:
E portanto, estabelece o que pretendíamos demonstrar.
T6 - (Radiciação)
[editar | editar código-fonte]
| ||
|---|---|---|
| Sejam a função , o limite da função em um ponto , quando a mesma está sob um radical de potência inversa , é: | ||
Demonstração:
Conseqüentes para funções algébricas:
Estas propriedades são verificadas rapidamente a partir da definição.
Além disso, as regras a seguir são conseqüências diretas dos teoremas relacionados acima:
sendo
sendo
Limites laterais
[editar | editar código-fonte]Consideremos a função: . Podemos notar que nenhum valor de menor que 2 está no domínio da função, ou seja, ela não está definida no intervalo . Esta indefinição também se refletirá nos limites dos valores da função neste intervalo, pois não faz sentido falar de "limites" em valores nos quais a função não esteja definida (neste exemplo, uma certa faixa de números reais).
O que poderíamos fazer para analisar os valores válidos da função?
Como o seu domínio é apenas , devemos restringir o cálculo de limites a este intervalo; quando um conjunto (no caso, um intervalo) de números precisa ser excluído do domínio da função, ou quando já se sabe que a função não está definida em tal conjuto, podemos também, excluir certa faixa de valores durante o cálculo de limites; Por exemplo, ao analisar o comportamento de nas proximidades do ponto , se quisermos adotar apenas números maiores que na análise, podemos simbolizar isto desta forma: , da mesma forma poderemos adotar apenas números menores que , representando a restrição da seguinte forma: .
No primeiro caso dizemos que o limite lateral pela direita da função é o valor para o qual a função tende quando se aproxima de pela direita. No segundo caso dizemos que o limite lateral pela esquerda da função é o valor para o qual a função tende quando se aproxima de pela esquerda.
Limite lateral pela direita
[editar | editar código-fonte]Dizemos que , quando:
Limite lateral pela esquerda
[editar | editar código-fonte]Dizemos que , quando:
Infinitos
[editar | editar código-fonte]Já lhe perguntaram o que é o infinito? Certamente alguém lhe deu uma resposta poética a respeito e de fato no sentido poético, o infinito é algo fascinante... Agora imagine um número absolutamente tão alto quanto é possível você conceber... Conseguiu? Pois bem, por maior que seja o número escolhido, ele não é infinito. Aqui, falaremos do infinito como sendo algo tão inatingível que nenhuma mente humana poderia imaginar. Infinito é uma tendência, uma forma de representar algo que é tão alto que jamais poderíamos atingir. É como se fosse um caminho sem fim, como o destino de um corpo sem obstáculos e atrito no espaço sem fim.
No início deste capítulo, discutimos como analisar o comportamento de uma função (sua tendência) quando a variável se aproxima de um determinado número. Nesta seção, discutiremos duas situações novas:
- O que acontece com os valores de , quando é muito grande?
- O que fazer quando, ao aproximar de um ponto , os valores de ficam cada vez maiores?
Usaremos o termo "infinito" sempre que for preciso lidar com "números gigantescos". Deste modo, também poderemos representar as duas situações acima usando conceitos de limite. Para isso, quando realizarmos um cálculo, podemos tratar o infinito como se fosse um número, embora ele seja um ente matemático que nunca poderemos alcançar. Por exemplo, caso a variável esteja tendendo ao infinito, e apareça em uma expressão, podemos imaginar o que aconteceria com a expressão caso fosse um número suficientemente grande. Então façamos um estudo de como podemos avaliar o comportamento das funções quando a variável tende a infinito.
Considerando uma função definida como:
Pensemos na melhor maneira de variar x para aumentar sucessivamente o valor desta função. Isto é possível fazendo com que forneça valores que diminuem até zero. É importante notar que quanto mais diminui, mais os valores da função aumentam.
Obviamente existem inúmeras formas de criar funções que aumentam seu valor sucessivamente. Usaremos esta pois nos ajuda a evitar expressões como quociente de funções complicadas ou composição de várias funções, e assim eliminamos dificuldades desnecessárias na análise dos resultados que veremos logo adiante.
Vejamos alguns exemplos numéricos de como a função aumenta sucessivamente os seus valores, quando a variável se aproxima de zero. Acompanhe a tabela:
| -2500 | -200 | -10 | -0,5 | -0,002 | -0,000016 | 0 | 0,00008 | 0,0025 | 2,5 | 250 | 4000 | |
| 0,0004 | 0,005 | 0,1 | 2 | 500 | 62500 | 12500 | 400 | 0,4 | 0,04 | 0,00025 |
Vemos que ao aproximar de zero, os valores de tendem a ficar muito grandes. No entanto, se tivéssemos utilizado a função em vez de , teríamos um comportamento ligeiramente para valores negativos de : Ao fazer se aproximar de zero, decresceria indefinidamente (tenderia a ).
Levando em conta a discussão anterior, formalizaremos expressões intuitivas como "os valores da função vão para o infinito", " tende ao infinito" e outras do gênero, com a notação , que será definida precisamente mais adiante.
Isto é um exemplo do que chamamos de infinito matemático.
Tendências infinitas
[editar | editar código-fonte]Neste ponto, nosso interesse é tratar da possibilidade de se aproximar de um certo número real, quando escolhemos valores cada vez maiores para . Um ótimo exemplo é a função apresentada acima. De acordo com a tabela, vemos que parece ser razoável escrever:
Isso se justifica, pois os valores de ficam muito pequenos (próximos de zero), quando é muito grande.
Este é um conceito importantíssimo na análise, no cálculo e em diversos campos das ciências exatas. Iremos aprofundar este conceito para formar ferramentas que serão úteis em diversos estudos. Para isso, considere a função . Pode-se mostrar que o seu valor jamais será maior que 1 quando tomamos valores de maiores que 1 (verifique!).
Fazendo sucessivas aproximações vemos que:
De fato temos uma tendência do valor da função se igualar a 1 quando levamos para números muito altos, embora ela nunca alcance o valor 1. Chamamos isso de limite no infinito, ou tendência infinita, e dizemos que tende a 1 quando tende ao infinito.
Podemos simbolizar a tendência de , quando fica cada vez maior, usando uma destas formas:
ou
O mesmo pode acontecer quando o valor da variável independente tende ao infinito negativo (), então podemos representá-la assim:
ou
A partir das noções apresentadas anteriormente, podemos definir de forma rigorosa as têndências infinitas e os limites infinitos.
Definição
Chamamos o número de limite lateral no infinito positivo se:
tal que vale a implicação
Ou seja, é o número para qual uma função tende a se igualar quando a variável independente ultrapassa o número positivo N.
Do mesmo modo, chamamos o número de limite lateral no infinito negativo se:
tal que vale a implicação
Os números são escolhidos de forma a fornecerem o maior valor possível dentro do domínio da função, que portanto deve necessariamente ser ilimitado.
Limites infinitos
[editar | editar código-fonte]Se nos depararmos com uma função onde o denominador decresce vertiginosamente até zero, o que podemos fazer?
Esta é a típica forma de funções que crescem até o infinito, neste caso adotamos o valor da definição de infinito, visto que não é possível colocar qualquer valor. Adotamos ou , pois , como já definimos anteriormente.
Continuidade
[editar | editar código-fonte]O básico conceito de continuidade expressa da ausência de quebras na regularidade da forma da função, quando apresentamo-la sob a forma gráfica. O que temos que ter em mente é que a função contínua em um intervalo do seu domínio é suavemente descritível, cada valor é precedido de outro menor ou maior, mas com uma discreta variação.
Ao definir o conceito de continuidade, o objetivo é identificar uma propriedade comum a diversas funções: a ausência de quebras ou saltos em seu gráfico. Geralmente exemplifica-se esta característica dizendo que uma função contínua é aquela "cujo gráfico pode ser traçado sem levantar o lápis do papel". Mas é importante ter em mente que isso é apenas uma interpretação do conceito, e que este é muito mais amplo.
|
Definição: (função contínua em um ponto) Se é definida num intervalo aberto contendo , então é dita ser contínua em se, e somente se . |
Para exprimir em símbolos que uma função é contínua no ponto , escreve-se:
Isto significa que:
Estas três condições estão presentes apenas em funções que não possuem irregularidades nas tendências e valores que produzem. As funções contínuas são muito comuns dentro do universo que analisamos, a condição de continuidade é exigida sempre que temos avaliar tendências a valores minúsculos.
Notas
[editar | editar código-fonte]- ↑ A ferramenta Wolfram|Alpha fornece mais informações computadas sobre "".
Derivadas
[editar | editar código-fonte]Funções são criadas para refletir o comportamento de certos entes físicos ou estados de valores, porém existe outro meio para analisar o comportamento dos números, que não conhecemos. Trata-se da derivação, um processo destinado a analisar as variações no comportamento de um conjunto de dados numéricos, largamente utilizado hoje em dia.
Vamos criar os conceitos, desde o início, para entender como estão fundamentados os princípios de derivação. Com estes teremos meios de analisar vários problemas sob a ótica infinitesimal (das pequenas variações).
Introdução (coeficientes angulares)
[editar | editar código-fonte]Seja uma reta definida pelos pontos e Existe uma relação entre as coordenadas dos dois pontos que expressa a inclinação da reta;
Definimos como coeficiente angular de uma reta, a seguinte razão:
O resultado desta relação é um número que expressa quanto a reta está inclinada comparada com o eixo x (da variável independente), pois quanto maior for o coeficiente angular de uma reta, mais próximo ela estará de ser uma reta vertical.
O coeficiente m é constante para qualquer segmento de uma reta fixada, e é visivelmente igual à tangente do ângulo formado entre a reta e o eixo x.
Agora imagine o que teríamos se ao invés de uma reta tivéssemos uma curva... Em uma função para a qual os pontos do gráfico não acompanham uma linha reta, geralmente temos diferentes valores de m para cada par de pontos que tomamos para fazer o seu cálculo. Isto se deve ao fato de que a inclinação varia ao longo da curva, o que nos sugere que cada pequeno segmento da curva possui um m diferente.
Considerando uma função teríamos sobre o seu gráfico os pontos:
Podemos denotar a distância de até por , e deste modo:
Logo, teríamos:
Esta relação nos dá a inclinação de cada segmento de reta ligando um ponto a outro estabelecida pela distância que nos fornece: Imaginando que o gráfico da função seja uma "curva suave", podemos, a partir da equação anterior, encontrar os valores de m e verificar qual a inclinação aproximada da curva para cada ponto; note que quando diminuímos o módulo de a equação se torna mais precisa, no sentido de fornecer uma melhor aproximação para o coeficiente angular de um pequeno trecho da curva, pois cada segmento que é analisado se torna menor, logo temos condições de analisar mais segmentos da curva.
Definição
[editar | editar código-fonte]Imaginemos que para cada par de pontos tenhamos uma reta, com seu respectivo coeficiente angular , como vimos anteriormente existe uma maneira de relacionar a declividade a cada ponto da curva...
Observe a figura a seguir, que mostra o gráfico da função e algumas retas secantes, passando pelo ponto onde e :
Podemos constatar que a função tem as seguintes características:
- A função f(x), expressa pelo gráfico, apresenta uma sinuosidade no intervalo entre e
- A função não apresenta qualquer ruptura ou salto neste intervalo.
Dada uma sequência de pontos cada vez mais próximos de , traçamos as retas , partindo do ponto fixado e passando pelos pontos correspondentes na sequência. Desta forma, podemos observar que, no caso da sequência apresentada na ilustração:
- A reta possui uma inclinação maior que ;
- Esta última possui uma inclinação maior que ;
Além disso, observamos ainda que:
- Quase não se consegue distinguir a reta do gráfico da função nas vizinhanças do valor de seu domínio, ou seja, esta reta parece uma boa aproximação da função em torno de
O que é importante saber é que os valores das inclinações das retas secantes se aproximam da inclinação de uma "reta tangente" ao gráfico da própria função no ponto a medida que diminui a distância entre um ponto da sequência e seu limite
Vemos então que uma maneira de tornar a inclinação da reta mais próxima da inclinação da função é diminuir a distância entre os pontos até o limite de sua aproximação, ou seja, se tomarmos uma sequência de pontos que ficam cada vez mais perto de , o resultado é que a partir de algum momento, os pontos tomados para o cálculo de m estarão tão próximos que cada um se tornará quase idêntico ao seguinte. Uma vez que se obteve um valor de m para cada ponto da sequência, gostaríamos de definir a inclinação de em , ou para ser mais preciso, a inclinação da reta tangente ao gráfico da função no ponto como sendo o limite:
Uma vez que tenhamos um valor deste limite para cada valor de de um certo conjunto, podemos criar uma nova função, que chamamos de função derivada de f, associando cada deste conjunto (o domínio da função derivada) com o correspondente (a inclinação de f neste ponto x). A nova função é obtida através dos valores de esse artifício de criar uma função que nos dá a declividade de uma outra função em cada ponto é chamado de derivação, uma vez que criamos uma função que é a derivada da primeira.
A diferença entre os valores de e quando levada ao limite próximo de zero, também é chamada de diferencial e a diferença entre os valores de e quando o diferencial é levado ao limite, é chamada de diferencial :
Por este motivo, esta operação é chamada de diferenciação, pois se refere à criação de variáveis diferenciais (usando as diferenças entre e ), neste caso e
Diferenciabilidade
[editar | editar código-fonte]Para que as diferenciais e por consequência, a derivada de uma função em um determinado ponto possam existir, certas condições devem ser cumpridas pela função. Verifica-se a partir da definição de que:
- Em primeiro lugar, o limite da função no ponto deve existir (verifique!);
- A função deve estar definida no ponto e seu valor ser igual ao limite;
Isso nos lembra a definição de continuidade. De fato, as condições acima significam que quando a função é diferenciável em um ponto, ela é também contínua no ponto.
O fato de funções derivadas serem contínuas se deve a existência do limite e do valor da função no ponto, uma vez que torna-se possível a existência do nestes casos.
Portanto, podemos em primeiro lugar verificar a continuidade de uma função para sabermos se há possibilidade da mesma ser diferenciável: se esta não for contínua temos condições de afirmar que a mesma não é diferenciável.
Regras básicas
[editar | editar código-fonte]Para simplificar os métodos de derivação algumas regras básicas são universalmente utilizadas, todas são consequências da definição e podem ser facilmente demonstradas através do limite que aparece na definição e dos teoremas sobre limites de funções.
T7 - Soma e subtração
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função sua derivada é: | ||
Demonstração:
Pela definição temos:
e portanto:
T8 - Multiplicação
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função então sua derivada é: | ||
Demonstração:
Pela definição temos:
Somamos e subtraímos na equação anterior:
e portanto:
T9 - Razão
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função então sua derivada é: | ||
Demonstração:
Pela definição temos:
Podemos lançar mão de mais um artifício algébrico e somar e subtrair o que nos dá:
Depois que aplicamos os limites, resulta em:
T10 - Natureza algébrica das diferenciais
[editar | editar código-fonte]
| ||
|---|---|---|
| Se existe, suas diferenciais podem ser tratadas como duas variáveis com características operacionais algébricas.
Seja e as diferenciais de sua derivada é: | ||
Seja e as diferenciais de quando sua derivada é Então:
Demonstração:
Pelo teorema da razão do limite:
O que nos dá a possibilidade de fazer:
Desta forma, os operadores e são limites e podem ser operados como tal, de forma que, obedecendo às regras das operações algébricas dos limites, podem ser separados.
T11 - Regra da cadeia
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função composta sua derivada pode ser calculada por: | ||
A função composta nos dá a possibilidade de generalizar diversas funções, permitindo a sua simplificação, a sua derivada pode ser conseguida pela relação
Que pode ser verificada quase que imediatamente através das propriedades algébricas das diferenciais, de qualquer forma podemos demonstrá-la como segue:
Para simplificar a interpretação do conteúdo, usaremos a notação de derivada em relação à variável dependente; nesta notação colocamos um D e um sobescrito da variável dependente, ou seja, o símbolo indica a derivada de z em relação a sua variável t.
Adotando esta notação para as derivadas, temos:
queremos e sabemos que para isso teríamos:
Quando ocorre que pois as duas funções são contínuas e u depende de x, logo:
então:
Derivadas algébricas simples
[editar | editar código-fonte]Podemos deduzir, a partir das regras comuns e da definição, equações que determinam a derivada para as funções mais comuns, adiante temos uma amostra destas equações e suas demonstrações.
T12 - constante
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função onde c é constante e portanto, independente de x, é demonstrável que sua derivada é nula, pois não existe variação do valor da função; | ||
Conforme constatamos:
T13 - fator
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função onde c é um fator constante e portanto, independente de x, é demonstrável que: | ||
- Demonstração
Façamos o cálculo pela definição:
Admitindo, inicialmente, que o ponto onde pretendemos encontrar a derivada tem e , logo:
O que nos afirma a validade do teorema.
T14 - Variável com expoente constante
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função onde é uma constante positiva e sua derivada é: | ||
Demonstração:
Temos pela definição:
Considerando o limite, temos:
Como única parte relevante, pois todas as outras terão valores nulos no limite, isto prova o teorema.
Diferenciação implícita
[editar | editar código-fonte]Considerando que as diferenciais podem ser tratadas separadamente e que temos meios para tratar ambas as variáveis de uma equação, a partir da regra da cadeia, temos instrumentos para diferenciar qualquer equação que represente uma função contínua. O método de diferenciação implícita é muito útil como meio de simplificar a resolução de diferenciais onde a variável dependente é de órdem superior.
A idéia mestra deste mecanismo é tornar implícito o conteúdo da variável, sem que seja necessária a sua substituição por equivalente algébrico antes da resolução; Vejamos um exemplo para simplificar a explanação:
A função é realmente complicada para ser diferenciada pelos métodos que vimos até agora, porém podemos esquecer a resolução da equação e considerar que a diferenciação pode, implicitamente, ser operada diretamente na equação inteira, desta forma:
A partir desta equação podemos operar as diferenciais algebricamente para encontrar o valor da derivada
A equação que representa a função apresenta dois valores possíveis para y:
O que nos dá duas derivadas, quando substituímos o valor de y na sua derivada:
Simplificando:
Desta forma podemos encontrar qualquer diferencial implicitamente, reduzindo a complexidade na aplicação das regras de derivação.
Aplicações das derivadas
[editar | editar código-fonte]Vamos começar a colocar em prática esses conceitos que aprendemos até então, a derivada de uma função é utilizada para diversas finalidades, algumas delas vamos explorar neste capítulo, porém não é possível generalizar as aplicações que podemos atribuir às derivadas, muitos recursos podem ser criados a partir dos seus conceitos, bastando para isto, a criatividade de cada mente a se manifestar.
A derivada é a medida da declividade de uma reta tangente a cada ponto da função de onde surgiu, ela também é uma função que fornece valores relativos de muita utilidade, podemos também lembrar que o ângulo da reta tangente ao ponto da curva inicial pode ser encontrado através da derivada, pois a derivada fornece o valor da tangente deste ângulo.
Enfim, temos muito o que extrair das derivadas, elas nos fornecem vários artifícios para manipular os números em uma função, possibilitando diversas maneiras de extrair informações, elas trazem um novo meio, capaz de nos trazer novas formas de analisar dados numéricos, vejamos o que podemos aproveitar de imediato...
Taxas
[editar | editar código-fonte]A maneira genérica de representar uma quantidade fracionada, o que nos leva a uma quantidade dentro de diversos conteúdos é a taxa ou relação; de maneira efetiva temos um total "x" de porções "T" em "n" recipientes, esta simples representação mostra como uma taxa é estabelecida:
A taxa é uma relação linear, que pressupõe o comportamento de dependência direta entre os termos; se tivéssemos que representar esta taxa em um gráfico, onde variássemos a quantidade de recipientes "n" e calculássemos o valor de "x", mantendo "T" constante, teríamos uma reta. É plausível pensar que a taxa "T" é constante, porém na natureza e no nosso cotidiano encontramos situações que raramente mostram a constância que observamos nesta equação, o mais comum é que tenhamos uma taxa diferente para cada situação em que nos deparamos.
Um caso típico, é a medida de velocidade de um corpo em movimento, se imaginarmos um carro andando pelas ruas de uma cidade, é impossível visualizar uma situação em que o carro tenha que se manter em velocidade constante por todo tempo que se mova a fim de chegar a seu destino. Uma vez que temos um ponto inicial e um final , além de um instante inicial e um final , também podemos calcular a velocidade média desenvolvida pelo veículo neste trajeto, que é:
ou
Agora imagine que tenhamos que medir tempos e distâncias cada vez menores, o que nos levaria a medir quase que instantaneamente os valores, então teríamos uma medida instantânea da velocidade, isto é equivalente a fazer com que o valor de se aproxime de zero:
Isto não nos lembra algo conhecido? Exatamente, uma derivada; a velocidade medida a cada instante é uma taxa tomada quando os tempos de medição se aproximam do limite entre um e outro, então teremos o valor da velocidade para cada instante, tal qual teríamos se estivéssemos observando o velocímetro do carro...
A constatação acima nos fornece um meio de calcular, a partir de valores sugeridos, o valor da velocidade instantânea, precisamos apenas da função "s" em função do tempo, depois podemos obter a derivada de "s" com relação a "t" e teremos:
Que é a velocidade instantânea de qualquer corpo que tenha seu deslocamento expresso pela função , todos os movimentos que um corpo físico pode desenvolver podem ser expressos sob este método de cálculo, uma vez que qualquer curva de deslocamento pode ser lançada na fórmula da derivada, podendo ser calculada em seguida.
Podemos ainda fazer o cálculo da aceleração do mesmo corpo:
O que nos dá a aceleração instantãnea:
ou
Note que ao derivarmos a função duas vezes estamos criando uma derivação dupla, que podemos simbolizar desta forma:
Esta expressão também é conhecida como "derivada segunda da função", o termo "segunda" designa o que chamamos de ordem da derivada, que indica quantas vezes a primeira função foi derivada, portanto temos o termo ordinal sempre indicando quantas vezes foi calculada a derivada.
Note que a derivação consecutiva de funções puramente algébricas sempre leva a zero, isto ocorre porque o grau do polinômio decresce até que reste apenas uma constante, a qual resulta em zero no último cálculo diferencial subseqüente.
Máximo, mínimo e médio
[editar | editar código-fonte]Considerando que uma função não constante deve ter um valor máximo e outro mínimo em um segmento de seu domínio, quais são as possibilidades de análise que teríamos com as suas derivadas, visto que estas expressam tendências da declividade da função?
Vejamos o que podemos extrair das derivadas de uma função, que são expressões da declividade da curva que a representa e nos intui a possibilidade de antever o curso dos valores da função ao longo do domínio.
Extremos de um intervalo
[editar | editar código-fonte]Seja a função cujo domínio limitamos em , a menos que seja constante,
(1) Há um número do intervalo cujo seu correspondente na imagem é menor que todos os outros no domínio.
(2) Há um número do intervalo cujo seu correspondente na imagem é maior que todos os outros no domínio.
Números críticos:
[editar | editar código-fonte]Definimos por número crítico, o valor assumido pela variável independente, de forma que seu resultante na imagem da função derivada seja nulo ou inexistente, o que na maioria das vezes se apresenta como um limite infinito.
Ou seja:
tem derivada e c é um número crítico da função se:
ou
T15 - Valor extremo
[editar | editar código-fonte]
| ||
|---|---|---|
| Considere agora que existe um número c, de forma que , que é domínio da função , podemos provar que:
Se ou Se então: | ||
Quando temos um número, dentro do intervalo, que obedece as condições acima, dizemos que é um "número crítico"; todas as vezes que uma função contínua tem um número cujo valor correspondente na imagem é maior ou menor que os valores dos outros, temos um máximo ou um mínimo no intervalo, intuitivamente, se a função é contínua e há um valor maior ou menor que os outros no mesmo intervalo é fácil concluir que a função terá que variar sua curva, variando a declividade de um valor positivo para outro negativo, o que nos leva a conclusão que, no limite entre os dois, ela terá que ser zero, fica claro então que quando há um extremo no intervalo, o valor numérico de sua derivada é nulo.
Vejamos a demonstração algébrica do teorema:
Seja os números , onde c é um número crítico do intervalo considerado, inicialmente, observando a derivada de , quando este valor é o maior no intervalo:
e da mesma forma:
O que nos leva a concluir que:
Por outro lado se é o menor valor do intervalo:
e da mesma forma:
O que nos leva a concluir que:
Logo em ambos os casos o limite que nos dá a derivada da função em c tem valor nulo.
Portanto sempre que temos um valor de uma função que é extremo em um intervalo, seja maior ou menor, este terá sua derivada nula.
T16 - Teorema de Rolle
[editar | editar código-fonte]Este teorema serve de base para outras demonstrações e observações, também sendo importante para conclusões ao longo do estudo.
Observe o gráfico:
Figura 3
Em decorrência do fato que a função gera dois valores iguais para a e para b, além de ser derivável, isto implica na existência de um número crítico c, entre estes dois pontos, visto que o teorema T15 demonstra este fato, além de afirmar que este extremo tem derivada nula, provamos que o teorema é valido para . Por outro lado se a derivada de também é nula, visto que quando o limite é alcançado, portanto:
T17 - Teorema do valor médio para derivadas
[editar | editar código-fonte]Tomemos dois números em um intervalo fechado , quando uma função é contínua neste intervalo temos pelo menos um número c, o qual projeta sobre a imagem da função um valor de forma que a sua derivada é igual ao valor da declividade da reta entre os pontos .
A explicação deste fato é facilmente observada no gráfico de qualquer função contínua em um dado intervalo, uma vez que a curva não apresenta rupturas ao longo de seu traçado e entre os pontos há pelo menos uma sinuosidade simples ou uma reta, haverá uma progressão continuada da declividade de um ponto em direção à declividade do outro, neste caso a curva terá sempre que reproduzir valores de declividade de um extremo a outro, de forma que teremos inevitavelmente um ponto cuja reta tangente será paralela a reta definida pelos dois pontos citados.
Algebricamente:
| ||
|---|---|---|
| Se onde m é o coeficiente angular da reta determinada pelos valores e seus conseqüentes na imagem da função: .
teremos: | ||
Análises de declive e concavidade
[editar | editar código-fonte]Uma interessante aplicação da derivada é a análise de tendências da função, o resultado desta derivada está ligado a declividade da reta "tangente ao ponto", uma vez que a tangente, nos dois primeiros quadrantes do plano cartesiano, apresenta uma distinção clara devido à mudança de sinal, isso possibilita uma boa gama de informações para a análise de seu comportamento e por conseqüência, da função que a originou.
T18 - Teste da derivada primeira
[editar | editar código-fonte]O coeficiente angular da reta que passa por um ponto da curva em uma função, nos revela uma tendência que varia conforme a tangente desta reta, tomando como referência o eixo x, quando a função é crescente os valores das derivadas para os mesmos, de x são sempre positivos, enquanto que quando a função é decrescente estes são sempre negativos. O que nos sugere o seguinte teste:
| ||
|---|---|---|
| Seja a função em um intervalo , dizemos que a função é crescente quando: | ||
Ainda podemos afirmar que, quando a função é decrescente: E finalmente, se a função não apresenta tendências, permanecendo inalterada até o limite do ponto: |
É possível provar o teorema, pela análise da definição da função derivada, da seguinte forma:
Se é contínua, existe tal que:
onde .
Admitindo que o denominador é positivo, ou seja, que , nos resta analisar o sinal do resultado no numerador, se e portanto, quando a função é crescente no intervalo, teremos , por outro lado se teremos uma função decrescente no intervalo e .
No último caso, se então a reta que passa pelo ponto é paralela ao eixo x, o que indica um extremo ou um ponto de transição na tendência de crescimento da curva; explicando melhor: Se os valores da função estão crescendo e o ponto em questão tem derivada nula, ou a função atinge o maior valor no intervalo, ou atinge um ponto de transição na tendência de crescimento, passando de crescente para decrescente; quando a função está decrescendo passa de decrescente para crescente.
T19 - Teste da derivada segunda
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função , dizemos que é a derivada segunda, com a qual podemos provar que:
Dado o intervalo , onde existe um número : | ||
Se então fornece o valor máximo no referido intervalo.
Ainda poderemos afirmar que: Se então fornece o valor mínimo no referido intervalo.
|
Análise:
Consideremos a derivada segunda .
Tomando o valor de podemos verificar o que ocorre com o numerador:
Se sabemos que a declividade da curva em é menor que a declividade de , como em c temos um valor crítico, temos que concluir que este representa um máximo, visto que os valores estão diminuindo quando são diferentes de c, ou seja, todos os valores decrescem a medida nos deslocamos no eixo x, portanto apenas pode assumir o valor máximo no intervalo.
Se sabemos que a declividade da curva em é maior que a declividade de , como em c temos um valor crítico, temos que concluir que este representa um mínimo, visto que os valores estão aumentando quando são diferentes de c, ou seja, todos os valores crescem a medida nos deslocamos no eixo x, portanto apenas pode assumir o valor mínimo no intervalo.
Concavidades
[editar | editar código-fonte]Temos formas côncavas em todo gráfico que apresenta variações, a derivada segunda também pode nos revelar outra característica interessante quando fazemos seu cálculo e a relacionamos à concavidade em um intervalo da curva... Como a derivada segunda reflete a tendência de crescimento ou decréscimo da declividade, temos como verificar que o seu sinal indica se a concavidade do gráfico é para cima ou para baixo, ou seja:
Se a concavidade da curva está voltada para cima.
Devido ao fato de que há uma tendência de crescimento da declividade naquele intervalo.
Se a concavidade da curva está voltada para baixo.
Devido ao fato de que há uma tendência de decréscimo da declividade naquele intervalo.
Pontos de inflexão
[editar | editar código-fonte]A inflexão é uma indefinição transitória das tendências da função em um determinado ponto, dizemos que o ponto onde a função passa da condição de tendência ao crescimento para tendência ao decaimento, ou vice versa, é chamado de ponto de inflexão. De forma geral, quando a função passa de uma taxa de variação positiva: ou negativa: ou vice versa, ela passa por um ponto de inflexão.
Considerando o número crítico c, para uma função , o ponto de inflexão é definido como aquele onde ocorre a inversão na tendência da declividade, ou seja, quando:
ou
Também é possível demonstrar que:
O que torna possível identificar o número crítico do ponto de inflexão a partir da derivada segunda da função.
Esboço de gráficos
[editar | editar código-fonte]Podemos aplicar os conceitos aprendidos neste capítulo para fazer esboços de gráficos, a prática deste artifício se mostra muito útil na análise de evoluções de grandezas, especialmente nas áreas de física, química e engenharia.
Para obter o gráfico de uma função qualquer pode-se usar de várias estratégias, entre elas: tabela de valores, uso de Cálculo, uso de ferramentas computacionais ou calculadoras gráficas.

Para usar o método da tabela, basta que num plano cartesiano sejam plotados pontos do gráfico da função em pequenos intervalos, unindo-os depois com uma linha "suave". Esboçar um gráfico assim não é muito recomendado se não se sabe com antecedência qual é o comportamento da função, visto que grandes flutuações podem ficar ocultas entre um ponto e outro. Por exemplo, se uma função for periódica (como , na figura ao lado) e o intervalo entre os valores for próximo ao do período dessa função (no caso, o período da função e o intervalo entre os pontos do domínio é 1), o esboço indicará uma função não periódica (), mas constante, claramente um erro. Por isso quando se utilizar desse método se deve ter cuidado para não se equivocar.
Para utilizar o computador ou uma calculadora, além da necessidade de saber como lidar com esse instrumento é necessário que se tenha certeza de que a função a ser esboçada não gerará nenhum bug no instrumento. Valores muito pequenos ou muito altos podem, dependendo do software, criar erros apreciáveis, os quais serão transmitidos para o gráfico a ser construído. Algumas funções podem acabar sem partes do gráfico, já que o programa não calcula a fórmula inserida em uma parte do domínio, mesmo que exista, devido a falhas ou mesmo omissões no código do aplicativo. Sendo assim, antes de usar o método é bom ter conhecimento a respeito do formato do gráfico, até mesmo para evitar erros decorrentes de digitação.
Para se utilizar o cálculo é necessário lembrar dos teoremas já estudados e também de suas implicações. É importante lembrar que os números críticos verificados com o teste da derivada primeira são diferentes dos conseguidos com a derivada segunda, podemos adotar uma notação indexada para identificá-los, assim temos: para o primeiro caso e para o segundo.
Para esboçar o gráfico de uma função desconhecida podemos extrair as raízes e o valor da função quando x é nula, além disso podemos verificar os pontos em que a função apresenta números críticos, extraindo a derivada primeira, a derivada segunda e resolvendo as equações: e , verificando os pontos onde as derivadas não existem; a partir de então podemos verificar as tendências de crescimento ou decaimento nos intervalos entre os números críticos, as raízes, pontos de inflexão e concavidades.
Obviamente, os resultados numéricos em pontos onde não existem números críticos não fornecem precisão para uma avaliação de valores, porém para a análise do comportamento da função e, em alguns casos, na visualização de formas geométricas, este método é bastante útil.
De um modo simplificado, pode-se estabelecer etapas para o esboço de gráficos com o uso de cálculo. 1. Expressar explicitamente a função a ser esboçada. 2. Calcular (algebricamente ou numericamente) as raízes da função, se existirem. 3. Procurar assíntotas horizontais, tomando o limite da função no infinito (tanto positivo quanto negativo) 4. Derivar a primeira vez e encontrar os pontos críticos da função (igualando a derivada a zero) 5. Derivar a segunda vez e testar os pontos críticos a fim de saber se são máximos ou mínimos locais (eventualmente globais) ou então se são pontos de inflexão. 6. Estudar o sinal da segunda derivada a fim de conhecer as concavidades da função original. 7. Representar as informações obtidas em um gráfico.
Integrais
[editar | editar código-fonte]Uma vez que podemos analisar a variação de determinados valores em uma função, como poderíamos reverter a análise, ou seja, se é possível criar uma função a partir de outra utilizando a diferenciação, o que teríamos se fizéssemos a operação inversa? Esta é uma questão que nos leva a mais um método do cálculo, a integração é uma forma de reverter a derivação, com ela temos um artifício para recuperar a função original a partir da sua derivada. Outra característica interessante da integral é que o valor numérico de uma integral definida exatamente em um intervalo é correspondente ao valor da área do desenho delimitado pela curva da função e o eixo x (abscissas). Vamos analisar em seguida como funciona o mecanismo básico de integração e nos capítulos seguintes nos aprofundaremos no tema, que é bastante vasto.
| Uma breve introdução dos conceitos que detalharemos neste capítulo pode ser encontrada em: |
Antiderivadas e antidiferenciais
[editar | editar código-fonte]Como procedemos para reverter a derivação? O princípio é verificado através da análise da inversão, da seguinte forma:
Considere a função cuja derivada , então dizemos que é a antiderivada de , a nossa primeira constatação é que a função primitiva inclui uma constante, que durante o processo de derivação é descartada, já que sua derivada é nula, se fizermos o processo inverso para obter a função original teríamos para operar e consegui-lo, isso nos leva a uma indefinição da função obtida através da antidiferenciação, a menos que conheçamos o valor da constante. Se quisermos obter a função original teríamos que operar e zero, o primeiro requisito é, a princípio, plausível de ser conseguido, porém operar zero para obtenção de qualquer constante parece algo não concebível.
Podemos então dizer:
A antiderivação é o processo pelo qual operamos a derivada de uma função para encontrar a sua exata função primitiva.
O que nos leva a conclusão que a antiderivação exige que tenhamos meios para encontrar a constante que pertencia a função quando ela foi derivada, ou que deduções, a partir de suas características e dos fenômenos utilizados para sua formulação, possam fornecer a constante.
A antidiferenciação, opera apenas os processos para dedução de um esboço da
função, o que chamamos de fórmula geral, no formato: .
Como podemos encontrar diversas constantes, temos diversas funções, o que nos dá a possibilidade de operar, por exemplo as funções: derivadas de , mesmo que , ao operarmos as funções derivadas utilizando a antidiferenciação teremos , que não nos garante meios de encontrar as primitivas, visto que não conhecemos meios para deduzir as constantes.
Definições
[editar | editar código-fonte]Ao operar a inversa da derivada, podemos fazer a análise com as diferenciais, ou seja, cosidere a função , então temos: , o que nos leva a algo muito interessante:
O que nos lembra:
Temos ainda que , fazendo-nos deduzir que precisamos operar:
Para encontrar y.
Esta operação é chamada de antidiferencial e é simbolizada por:
Onde (f) é a função e (d) é a diferencial da variável independente.
De forma mais completa a antidiferencial da função é:
onde C é a constante que define a função primitiva.
Operações básicas
[editar | editar código-fonte]A antidiferenciação é uma operação que tende a ser complicada na maioria das funções, ao longo do nosso estudo veremos métodos para simplificar o processo, porém existem formas de funções que não podem ser operadas nesse processo. Algumas das regras básicas para operação de antidiferenciais serão abordadas nas seções subseqüentes, outras regras serão abordadas nos próximos capítulos. Devido a complexidade que envolvem o processo, muitos dos métodos necessitam de alguma regra que ainda não estudamos; para não colocar questões que não possam ser esclarecidas neste capítulo teremos que deixá-las para o momento oportuno, quando todos os elementos necessários para a abordagem do assunto estejam bem claros.
T20 - Diferenciais
[editar | editar código-fonte]
| ||
|---|---|---|
| A diferencial ao ser operada pela antidiferenciação, resulta: | ||
Com C constante.
Comprovação:
De fato se :
T21 - Constantes
[editar | editar código-fonte]
| ||
|---|---|---|
| A constante c é operada como coeficiente da variável independente, de forma que sua antidiferencial é: | ||
Comprovação:
Se fizermos: , teremos:
Conforme o teorema T13 - fator.
T22 - Adição
[editar | editar código-fonte]
| ||
|---|---|---|
| Se então: | ||
Comprovação:
Se é o resultado da soma de duas antidiferenciais, logo:
- Temos que admitir que e são diferenciais;
- A soma de diferenciais admite que:
- Se e , temos:
- Sendo, portanto, possível fazer:
- Além disso: Se então, podemos fazer:
Portanto, pela análise da reversibilidade, é possível constatar que a adição de duas antidiferenciais pode ser operada distributivamente, o que atesta a regra que expomos.
T23 - Variável com expoente constante (antidiferencial)
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função onde n é constante, sua antidiferencial é: | ||
| ; onde: |
Onde C é constante.
Comprovação:
T24 - Regra da cadeia para antidiferenciais
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja as funções e , contínuas em seus domínios ou no intervalo a que se propõe a análise em questão. A antidiferencial da função composta com relação a x é: | ||
Onde C é a constante que define a primitiva.
Comprovação:
Uma vez que:
, temos:
O que nos possibilita operar, por substituição:
, obtendo:
para definir a antiderivada, usamos a constante C:
O que comprova a regra.
Introdução a equações diferenciais
[editar | editar código-fonte]Considerando a questão da indefinição criada pela diferenciação, o processo de antidiferenciação traz uma conseqüência indesejável para o processo de equacionamento de diferenciais. Quando uma equação diferencial é proposta, a constante de antidiferenciação faz com que o processo de resolução seja bastante prejudicado, o que exige que tenhamos técnicas especiais para tentar resolvê-la. Faremos agora uma breve introdução aos conceitos de equações diferenciais, porém, o estudo completo do tema demanda um aprofundamento maior por parte dos interessados, ao longo dos nossos estudos teremos meios para simplificar o processo, embora que a solução de muitas equações diferenciais quando não são impossíveis exigem muito esforço e dedicação.
Diferenciais de primeira ordem
[editar | editar código-fonte]Seja a equação , a sua derivada é expressa como:
sendo uma constante arbitrária, definida pelas características das deduções que originaram a equação.
O que resulta na equação diferencial:
Esta equação é denominada: Equação diferencial de primeira ordem, visto que é originada de uma derivada primeira, o que permite facilmente separar as variáveis diferenciais. Por outro lado, como meio para reverter o processo de diferenciação, fazemos:
Com C constante; lembre-se que C é uma constante não definida, a constante original é .
Pelo exposto deduzimos que a equação assumirá a forma:
Porém, como C é uma constante indefinida, temos uma função ainda indefinida.
Constante antidiferencial
[editar | editar código-fonte]A constante resultante da indefinição na antidiferenciação é expressa na equação diferencial como observamos na seção anterior, para aumentar as possibilidades da análise, cosideremo-la como variável, ao fazer isto temos um comportamento interessante para a função resultante; quando atribuimos valores a esta variável temos uma equação para cada valor assumido pela mesma, se observarmos mais atentamente, descobriremos que o gráfico da função mantém a forma, porém varia a altura em relação ao eixo das abscissas (variável independente), ou seja, a equação antidiferencial fornece um conjunto de curvas, o que possibilita uma infinidade de valores.
O que definiria a escolha de uma constante em particular? A constante definirá qual a curva que obedece o comportamento espelhado pelos números que compõem a curva a ser escolhida. De fato basta um par ordenado definido dentro do conjunto de números que obedecem à equação e teremos a definição da função exata. Em várias áreas onde podemos utilizar estas equações temos a definição deste par ordenado a partir do comportamento dos números que são observados ou deduzidos, na maioria das vezes este par de números é chamado de estado inicial, pois estabelece o comportamento da equação quando os valores das variáveis são conhecidos inicialmente.
No nosso caso da seção anterior coseguimos a fórmula geral:
Certamente, podemos afirmar que:
Quando temos pois:
É uma afirmação fácil de ser encontrada, uma vez que conhecemos a equação original, porém se não a conhecemos, a observação e a dedução lógica devem ser usadas para encontrá-la. Algumas vezes podemos nos perguntar: Basta-nos conhecer o conjunto de equações ou precisamos de uma equação específica? O mérito desta questão deve ser avaliado de acordo com a necessidade da análise a ser feita, cabendo ao analista verificar quais são seus requisitos dentro do que se propõe a verificar.
A integral indefinida
[editar | editar código-fonte]Seja a antidiferencial:
Observamos que a mesma corresponde a uma operação sobre pequenas seções de área, pois corresponde a multiplicação de um segmento numérico de largura, , pela altura, o valor da função aproximada ao limite em cada ponto.
A operação da forma que se apresenta estende-se de a . Analisando qual a natureza desta operação, podemos tomar dois valores para , sejam: e , sendo , quando analisamos este fato concluimos que a área do intervalo menor está dentro da área do maior, vemos que a operação comporta-se como uma soma de áreas, se somarmos todas as componentes de áreas ao longo da curva teremos uma área delimitada pela curva e o eixo x.
Chamamos esta operação de integral, seu símbolo é o mesmo da antidiferenciação, pois devido aos fatos acima introduzidos e ao teorema fundamental do cálculo, que discutiremos adiante, a operação de antidiferenciação pode ser chamada de integral indefinida.
A integral definida
[editar | editar código-fonte]Aprofundando o conceito de que há uma soma de pequenos segmentos de área para cada ponto em uma curva, podemos delimitar uma seção da curva, através da adoção de um intervalo, desta forma teremos uma área definida, a qual chamamos de integral definida. Antes de detalhar o processo para encontrar a referida área faz-se necessário a observação de conceitos que serão úteis para seu desenvolvimento, o próximo tópico abordará a somatória, um procedimento que facilitará o estudo das somas sucessivas que propomos analisar.
Somatórias
[editar | editar código-fonte]Considere a operação: , chamamos esta operação de somatória, ela é simbolizada pela letra grega sigma (), utilizando a notação escrita como segue:
O significado deste símbolo é facilmente compreendido: A variável i é chamada de índice, o número n é a quantidade de parcelas, ocorre que, ao substituir estes valores na expressão , fazemos de forma seqüencial, somando um valor ao anterior, como descrito na operação acima, o que resultará no valor final de U, pretendido na referida operação.
Propriedades
T25 - Constante
[editar | editar código-fonte]
com c constante.
Comprovação:
n vezes.
T26 - Fator
[editar | editar código-fonte]
com c constante.
Comprovação:
T27 - Adição
[editar | editar código-fonte]
Comprovação:
T28 - Exclusão de termo antecedente
[editar | editar código-fonte]
Comprovação
Definição da Integral de Riemann
[editar | editar código-fonte]O conceito de integral está ligado à necessidade de encontrar a área de curvas, as abordagens tomadas para solucionar o problema do cálculo de áreas curvas encontram sempre o mesmo resultado. Para não nos extendermos muito, faremos uma explanação do processo chamado: Integral de Riemann, o qual é um dos mais conhecidos.
Vejamos o gráfico abaixo:
Figura 4
O gráfico mostra uma função sinuosa, se fizermos seções retangulares para imitar o contorno das curvas teremos uma maneira grosseira de calcular a área delimitada pela curva e o eixo x, uma vez que temos a possibilidade de aumentar a quantidade de retângulos, podemos aumentar a precisão dos nossos cálculos... Se fizermos com que o número de retângulos aumente numa tendência ao infinito, teremos o valor da área.
Consideremos a função do gráfico: , a sua integral entre os valores de x: a e b é:
Chamamos o intervalo de partição e simbolizamos como: . Ao dividirmos o intervalo em n "pedaços"(seções) temos a possibilidade de definir o tamanho de cada um, porém a regra de Riemann é mais flexível e estabelece que podemos ter pedaços de tamanhos diferentes, de forma que tenhamos apenas que estabelecer os valores de x tal que: . Uma vez que estabelecemos os valores dos x, podemos arbitrar um ponto intermediário entre eles para que seja o ponto onde definiremos o valor da função, este ponto será importante porque ele estabelecerá a altura do retângulo. O valor de x, que determinará o ponto da altura de cada retângulo é referenciado como , referenciamos estes pontos como: .
A base dos retângulos é , onde os valores podem variar livremente, porém há sempre um retângulo que possui a maior base, que chamamos de norma da partição , simbolizada por .
Podemos somar todos os retângulos da partição, fazendo o cálculo aproximado da área, da seguinte maneira:
A integral é obtida quando fazemos os retângulos tão pequenos que poderemos considerar suas bases quase nulas, para isso podemos dividir a partição em pedaços de :
O que nos permite delimitar a norma e definir a sua tendência a zero, também nos dá a possibilidade de definir a integral como:
Propriedades da integral definida
[editar | editar código-fonte]Algumas propriedades são observadas a partir dos conceitos expostos sobre a integral, são regras para simplificar algumas operações, mas que podem ser úteis para o estudo de teoremas que veremos em capítulos mais adiante, vejamos as propriedades e suas comprovações:
Sejam e , funções contínuas no intervalo , podemos afirmar que:
T29 - Limites iguais
[editar | editar código-fonte]
Comprovação:
Podemos observar que, ao tomarmos o intervalo , dividindo-o em n pedaços, teremos:
Sendo teremos:
então:
e:
O que comprova o teorema.
T30 - Fator do integrando
[editar | editar código-fonte]Sendo K constante:
Comprovação:
que é igual a:
O que comprova o teorema.
T31 - Inversão dos limites
[editar | editar código-fonte]
Comprovação:
Novamente tomando o intervalo , dividindo-o em n pedaços, teremos:
Portanto é fator determinante do sinal. Se tomarmos a integral no intervalo e invertermos a sua posição no cálculo, teremos:
Logo, tomando como é igual a tomar como .
O que comprova o teorema.
T32 - Adição
[editar | editar código-fonte]
Comprovação:
Sendo a integral:
logo:
O que comprova o teorema.
T33 - Seções complementares
[editar | editar código-fonte]Sendo c constante e :
Comprovação:
Tomando o intervalo entre a e c e fazendo a relação:
e
O é um valor que pode ser atribuído às duas relações, portanto podemos fazer:
Que é semelhante a propriedade da soma das áreas de dois objetos que formam um corpo maior, que costumamos usar na geometria e que prova o teorema.
T34 - Valor médio
[editar | editar código-fonte]Seja a seção no domínio da função , dizemos que M é o valor médio da função neste intervalo, sendo seu valor definido como segue:
Comprovação
O valor médio de uma função é expresso pela função abaixo:
Onde representa um valor em particular. Sendo o valor da função para cada retângulo, podemos fazer a sua média da seguinte forma:
Por outro lado, podemos fazer com que o n seja:
logo:
Uma vez que o é um valor muito grosseiro, podemos encontrar o limite quando a norma da partição tende a ser nula, desta forma:
O que comprova o teorema.
T35 - Teorema fundamental do cálculo
[editar | editar código-fonte]Seja a função contínua no intervalo , a sua integral definida entre a e b é obtida pela operação que segue:
Onde:
Chegamos ao ponto culminante deste estudo inicial sobre as integrais, este teorema, chamado de Teorema fundamental do cálculo, é a base de nossas análises mais específicas nos próximos capítulos, ele afirma que a integral definida pode ser obtida através da antidifererncial da função, para tal, adotamos a seguinte notação :
Comprovação:
Devemos demonstrar que a derivada de é igual a .
Como podemos observar, quando calculamos o valor da integral definida, variamos o limite superior gradativamente de a até b, isto nos indica que podemos criar uma nova função, como escrito abaixo:
Observe que x é dita independente de u, pois a última constroi a curva da função, enquanto que a outra nos dá a integral de qualquer ponto com relação a distância da contante a, portanto, calculando sua derivada temos:
Conforme o teorema T34, a parte da equação operada pelo limite é um valor médio.
Observe que , ou seja, é o limite do valor médio quando o intervalo tende a ser nulo, o que resulta em , pois é equivalente a fazer uma média com apenas um elemento, o próprio valor de . Observemos ainda que o valor médio, aqui expresso, não é constante, visto que depende de x, o que quer dizer que temos um valor médio para cada seção da curva.
O valor médio dos valores entre e no mínimo é feito com os dois extremos apresentados, da seguinte forma:
e
no limite:
resulta:
.
Portanto é antidiferencial de .
Por outro lado ao fazer:
então: que é a antidiferencial de , logo:
O que comprova o teorema.
O estudo das funções deste capítulo refere-se às funções não puramente algébricas, relacionadas a números transcendentais, algumas das quais já conhecemos da matemática elementar, porém é necessário um aprofundamento do tema para o ambiente acadêmico, onde temos que lidar com análises mais detalhadas e complexas.
Logarítmicas
[editar | editar código-fonte]A integral da função algébrica traz uma indefinição quando :
A existência desta indefinição nos leva a uma questão: Qual o procedimento para integrar a função: ? A resposta é dada na análise numérica, calculando a integral pelos métodos de análise algébrica podemos chegar a seguinte conclusão:
A função ln é chamada de logaritmo natural, a sua base é chamada de número de Euler, ele é um logarítmo conseqüente do cálculo da área sob a curva da função , que pode ser obtido numericamente usando a integral de Riemann e outras técnicas de cálculo numérico. Aproximações deste número são possíveis utilizando-se técnicas de aproximações sucessivas com o uso de séries, discutidas em Cálculo (Volume 3).
Todos os teoremas para logaritmos, que estão incluidos nos cursos de nível médio, podem ser obtidos a partir da análise do logaritmo natural, também chamado de logaritmo Neperiano.
Teoremas
[editar | editar código-fonte]Vejamos os principais teoremas para os logaritmos:
Nas citações abaixo, consideremos ,
T36 - Produto
[editar | editar código-fonte]
Comprovação:
Da definição:
fazendo e quando :
O que comprova o teorema.
T37 - Razão
[editar | editar código-fonte]
Comprovação:
Sendo :
logo:
T38 - Potência
[editar | editar código-fonte]
Comprovação:
Sendo:
-> b vezes, que é:
-> b vezes, resultando:
Derivadas
[editar | editar código-fonte]Da definição do logarítmo natural e a partir do teorema fundamental do cálculo, podemos deduzir a derivada da função logarítmica natural, ou seja, se que é a integral definida de , então a derivada é:
Integrais
[editar | editar código-fonte]Para integração de funções logarítmicas, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.
Exponenciais
[editar | editar código-fonte]A função é chamada de função exponencial na base a, todas as funções exponenciais são introduzidas a partir da definição do logaritmo natural ln x como sua função inversa. As funções exponenciais são estas em que a parte variável é o logaritmo, ou seja:
Se
então:
O que implica , tornando-o uma função, na qual podemos atribuir valores a x e obter uma imagem. O número a é chamado base, este número é facilmente identificado nos logaritmos convencionalmente abordados na matemática elementar, mas qual é a base da função ?
Esta questão nos leva a um novo conceito abordado na próxima seção, o número de Euler.
O número de Euler
[editar | editar código-fonte]A base do logarítmo natural é o número de Euler, simbolizado por: e, ele é obtido pela definição do logaritmo natural, esse número corresponde á área sob a curva da função: , quando seu valor é unitário, ou seja:
,
mais formalmente:
O valor deste número pode ser encontrado por aproximação, utilizando-se os métodos de análise de seqûencias e séries, encontrados no livro: Cálculo (Volume 3).
A equação que fornece o valor do número de Euler é dada a seguir:
Nesta equação podemos observar que quanto mais alto o valor de n mais preciso se torna o valor de e.
De maneira simplificada, com base nos conceitos até agora abordados podemos encontrá-la da seguinte maneira:
Se então , logo:
Por outro lado, pela definição:
Para :
Sendo: e
Concluimos que:
Teoremas
[editar | editar código-fonte]A maioria dos teoremas relacionados, têm origem nas conclusões obtidas no estudo do logarítmo natural, dos quais relacionamos os mais usados:
T39 - Soma
[editar | editar código-fonte]Seja a função , pode-se afirmar que:
Comprovação:
Considerando: e ,
logo:
sendo: e ,
O que comprova o teorema.
T40 - Subtração
[editar | editar código-fonte]De forma similar à análise anterior, sendo a função , pode-se afirmar que:
Comprovação:
Considerando: e ,
logo:
sendo: e ,
O que comprova o teorema.
T41 - Potência
[editar | editar código-fonte]Seja a função , pode-se afirmar que:
Comprovação:
O que comprova o teorema.
Derivadas
[editar | editar código-fonte]Consideremos que , e conseqüentemente: , se derivarmos implicitamente este expressão:
Curiosamente, teremos:
Ou seja, a função exponencial natural é invariável durante o processo de derivação, o que traz uma série de implicações simplificadoras para estas funções.
Por outro lado se , temos que:
Fazendo e , teremos:
Se , concluimos que:
Que é adotada como uma derivada mais genérica, pois pode ser empregada em qualquer exponencial, pois inclui correção para o fator da base.
Integrais
[editar | editar código-fonte]Como não poderia ser diferente, o valor da integral da função exponencial natural é a própria função, conforme a regra da reversibilidade entre a derivada e a integral, apenas sendo necessária a devida observação da base, para eventual correção da diferencial e conseqüente introdução de fator de correção, nos casos em que a função torna-se composta.
Desta forma, temos:
,
Sendo C constante.
Logarítmicas com outras bases
[editar | editar código-fonte]Como foi visto durante o ensino médio, os logaritmos têm uma definição direta e que denota a sua finalidade de expressar o valor do expoente em uma operação exponencial, a definição pura é dada da seguinte forma:
Se então,
Onde: a é chamada base do logaritmo, x é o logaritmando e n é o expoente.
O logaritmo é, portanto, a operação pela qual se obtém o expoente necessário para que a base seja elevada, numa operação exponencial e se obtenha o número x.
A função logarítmica de base a pode ser expressa da seguinte forma:
O que nos possibilita encontrar um valor para cada x expresso na equação.
Mudança de base
[editar | editar código-fonte]Analisemos agora a possibilidade de encontrar uma função logarítmica de uma base a e transformá-la em uma função logarítmica de base natural, ou outra base qualquer:
Seja a função , podemos dizer que:
e que ,
como: ,
,
,
,
O que nos possibilita afirmar que:
,
ou
.
Note que a analogia serve para funções logarítmicas de qualquer base, visto que podemos substituir por sendo z a base que substituirá e na análise anterior.
O que nos possibilita considerar que quando temos duas bases, sejam: a e b, podemos promover a troca das bases, de forma que:
Derivadas
[editar | editar código-fonte]A derivada da função logarítmica com base diferente de e pode ser feita por substituição da base. Considerando , temos que:
,
,
logo:
Que nos dá a derivada:
Trigonométricas I
[editar | editar código-fonte]A trigonometria, tal qual vista na matemática elementar, está relacionada com as relações métricas do triângulo retângulo e do ciclo trigonométrico, agora introduziremos o estudo infinitesimal das funções trigonométricas que são largamente utilizadas nas ciências exatas.
Conceitos básicos (Radianos)
[editar | editar código-fonte]Em um plano definido pelos eixos x e y podemos estabelecer coordenadas cartesianas para cada ponto, o que nos permite identificar cada um dos pontos em qualquer posição do plano, existe outra maneira de encontrar um ponto neste plano; se quisermos estabelecer uma relação triangular podemos determinar a posição de cada ponto no plano da seguinte forma:
Figura 5
Imagine que cada ponto está numa distãncia R do ponto em um plano cartesiano definido por pontos , da mesma forma a reta R, que é definida entre os pontos , forma um ângulo com o eixo x, que chamaremos de , note que podemos identificar qualquer dos pontos no plano a partir de uma reta R e um ângulo .
Observemos que R, quando fixa, é uma reta que determina um conjunto de pontos em torno do ponto , se fizermos variar em todos os valores possíveis teremos uma circunferência. Quando fazemos o valor de R variar teremos diferentes valores de x e y, porém a relação entre eles sempre será a mesma.
Curiosamente, há uma relação entre o perímetro do círculo e o seu diâmetro, ela se apresenta constante qualquer que seja o raio do círculo; o resultado desta relação é um número transcedental chamado PI, representado pela letra grega de mesmo nome: . Resgatando esta relação para a nossa análise podemos dizer que, se chamarmos o perímetro da circunferência, formada no gráfico, de e admitirmos um diâmetro de , então teremos:
Que resulta em:
Que é uma relação bastante esclarecedora, visto que nos mostra uma dependência linear entre o raio e o comprimento de um fio imaginário que pudesse ser usado para seguir o contorno da circunferência do gráfico. Se o raio for unitário teremos um valor de referência para l, que poderá ser usado para encontrar qualquer comprimento de circunferência no gráfico, bastando para isto multiplicá-lo pelo raio, este valor de referência está ligado à circunferência fechada. Por outro lado, se fizermos com que R se desloque de um ângulo nulo, ou seja, que saia do eixo x em direção a y, formando um ângulo , teremos pedaços de circunferência, que chamamos de arcos, considerando que temos um raio unitário e que percorremos um pedaço da circunferência para cada ângulo "" que tomamos, temos uma correspondência entre ângulo e arco, ou seja: podemos nos referir a arcos como unidades de ângulos, esta unidade angular é chamada de Radiano. Qualquer círculo forma radianos e todas as relações entre os pontos da circunferência que o contorna e os eixos cartesianos podem ser referenciadas como relações entre partes desta medida.
Como o radiano é uma medida real, isto nos leva a outra questão: O que determina o sinal negativo ou positivo neste valor?
Acontece uma variação destes valores quando nos deslocamos de um ponto a outro da circunferência, quando saimos do eixo x em direção ao ponto o ângulo cresce, portanto temos que concluir que é positivo, recuando-o ao encontro do eixo x os valores diminuem, portanto se ultrapassarmos o eixo x o valor deve ser menor que zero, nos revelando um ângulo negativo.
Seno e cosseno
[editar | editar código-fonte]Temos, portanto, uma circunferência dentro do plano cartesiano e seus pontos relacionados ao raio R e ao ângulo , são referenciados pelas variáveis x e y no mesmo plano, agora imaginemos funções para que seja possível a partir do raio e do ângulo encontrar as variáveis, estas funções são o seno e o cosseno.
A função seno, simbolizada como:
Nos dá o valor da variável y, ou seja, a altura do ponto em relação ao zero referencial, no encontro dos eixos, conforme espelhada no eixo y, quando o raio R é unitário, caso não seja fazemos .
A função cosseno, simbolizada como:
Nos dá o valor da variável x, ou seja, a distância do ponto em relação ao zero referencial, no encontro dos eixos, conforme espelhada no eixo xquando o raio R é unitário, caso não seja fazemos .
As funções seno e cosseno são periódicas, ou seja, pela natureza do ciclo trigonométrico, quando temos um valor em x maior que temos a representação de um ciclo completo mais um ângulo residual, na verdade o valor representa este ângulo residual, o que nos leva a constatação que sempre será calculado o valor do seno ou cosseno do resto da operação quando um ângulo maior que for sugerido para x.
Alguns valores de senos e cossenos de certos arcos são perfeitamente dedutíveis através da observação do ciclo, são eles:
| Ângulo | 0 | |||
|---|---|---|---|---|
| 0 | 1 | 0 | -1 | |
| 1 | 0 | -1 | 0 |
Observando o gráfico podemos também concluir que o sinal do seno é idêntico ao sinal do ângulo, enquanto que o cosseno não acompanha o sinal do ângulo, de forma que cossenos de ângulos negativos são iguais a cossenos dos valores absolutos dos ângulos, ou seja:
sendo ,
enquanto que:
Outros senos e cossenos podem ser obtidos pelas relações métricas no triângulo e são largamente utilizados, são:
| Ângulo | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
Identidades (1)
[editar | editar código-fonte]As equações desta seção são conseqüência das características dos senos e cossenos, seu comportamento cíclico e sua relação com uma circunferência de raio unitário lhes conferem uma excelente operatividade, possibilitando-nos fácil intercâmbio entre as mesmas.
I-1 Identidade relacional básica
[editar | editar código-fonte]As funções seno e cosseno estão relacionadas pela equação:
Comprovação:
Observando o ciclo trigonométrico, temos um triângulo cujos catetos são: e e sua hipotenusa é 1, portanto a identidade é conseqüente do conhecido teorema de Pitágoras.
I-2 Cosseno da soma
[editar | editar código-fonte]Sejam os ângulos a e b, o cosseno de sua soma é[1]:
Comprovação:
Nos pontos A e B do ciclo trigonométrico, temos os arcos para os ângulos a e b:
Figura 6
A distância entre os pontos P e (A+B) é igual à distância entre -A e B, o quadrado das duas é:
Da identidade básica:
Como e :
O que comprova a identidade.
I-3 Cosseno da diferença
[editar | editar código-fonte]Sejam os ângulos a e b, o cosseno de sua diferença é[2]:
Comprovação:
Do cosseno da soma:
Substituindo b por -b:
O que comprova a identidade.
I-4 Equivalência angular
[editar | editar código-fonte]Se o ângulo a é e b é x, então:
logo:
Por outro lado, se:
e
, obtemos:
I-5 Seno da soma
[editar | editar código-fonte]Sejam os ângulos a e b, o seno de sua soma é[3]:
Comprovação:
Sendo e , temos:
O que comprova a identidade.
I-6 Seno da diferença
[editar | editar código-fonte]Sejam os ângulos a e b, o seno de sua diferença é[1]:
Comprovação:
Se ,
Substituindo b por -b, temos:
e enquanto que , logo:
O que comprova a identidade.
I-7 Produto de dois senos
[editar | editar código-fonte]Sejam os ângulos a e b, o produto de seus senos é[4]:
Comprovação:
Considerando a identidade do cosseno da diferença de dois ângulos e subtraindo de cada um de seus membros os membros correspondentes da identidade do cosseno da soma de dois ângulos:
O que comprova a identidade.
I-8 Produto de dois cossenos
[editar | editar código-fonte]Sejam os ângulos a e b, o produto de seus cossenos é[5]:
Comprovação:
Considerando a identidade do cosseno da soma de dois ângulos e somando a cada um de seus membros os membros correspondentes da identidade do cosseno da diferença de dois ângulos:
O que comprova a identidade.
I-9 Produto de seno e cosseno
[editar | editar código-fonte]Sejam os ângulos a e b, o produto do seno de a pelo cosseno de b é[6]:
Comprovação:
Considerando a identidade do seno da soma de dois ângulos e somando a cada um de seus membros os membros correspondentes da identidade do seno da diferença de dois ângulos:
O que comprova a identidade.
I-10 Soma de dois senos
[editar | editar código-fonte]Sejam os ângulos p e q, a soma dos senos de p e de q é:
Comprovação:
Podemos dizer que:
substituindo na identidade:
O que comprova a identidade.
I-11 Soma de dois cossenos
[editar | editar código-fonte]Sejam os ângulos p e q, a soma dos cossenos de p e de q é:
Comprovação:
Seguindo a analogia anterior:
O que comprova a identidade.
I-12 Diferença de dois senos
[editar | editar código-fonte]Sejam os ângulos p e q, a diferença dos senos de p e de q é:
Comprovação:
substituindo q por -q em:
O que comprova a identidade.
I-13 Diferença de dois cossenos
[editar | editar código-fonte]Sejam os ângulos p e q, a diferença dos cossenos de p e de q é:
Comprovação:
substituimos q e q, por e em:
O que comprova a identidade.
Limíte trigonométrico fundamental
[editar | editar código-fonte]Precisaremos de um limite fundamental nas próximas seções, se trata de um limite que é utilizado na dedução das derivadas do seno e do cosseno, faremos sua dedução nesta seção. Considere o ciclo trigonométrico representado a seguir:
Figura 7
A figura 7 mostra a representação de um ângulo no ciclo trigonométrico, o nosso propósito é deduzir o seguinte limite:
Para isto, imagine o triângulo inscrito na circunferência, podemos dizer que o segmento de reta n é uma aproximação grosseira do arco , porém observe que quando o ângulo se aproxima de zero o segmento se torna mais parecido com o respectivo ângulo, algébricamente podemos expressar que:
Por outro lado façamos o cálculo do valor do n; observando o triângulo podemos dizer que:
Logo:
Simplificando temos:
Voltando para o nosso limite, temos que usar as nossas equações anteriores desta forma:
Substituindo o valor do seno no lado da equação relaciondado ao n, teremos:
O que nos leva ao resultado:
A interpretação desse limite é a seguinte:
Uma vez que o ângulo diminui até valores próximos de zero e o arco tende a se assemelhar a uma reta em regiões próximas do zero, o valor do seno é igual ao valor do arco no limite, quando o seu valor se aproxima de ser nulo.
Derivada do seno
[editar | editar código-fonte]Agora podemos verificar qual a variação da função seno em relação ao seu ângulo, aplicando a definição da derivada ao seno, temos:
Aplicando o seno da soma:
Aplicando os limites:
Temos, então, o limite fundamental que é igual a 1, logo:
Derivada do cosseno
[editar | editar código-fonte]Também podemos verificar qual a variação da função cosseno em relação ao seu ângulo, aplicando a definição da derivada ao cosseno, temos:
Aplicando o seno da soma:
Aplicando os limites:
Novamente temos o limite fundamental, logo:
Integral do seno
[editar | editar código-fonte]Como conseqüência do resultado da derivada do seno, podemos deduzir que a sua integral, como operação inversa é:
Cuja constante C é a constante devido a indefinição no processo de antidiferenciação, conforme já estudamos anteriormente.
Integral do cosseno
[editar | editar código-fonte]Segundo o mesmo princípio colocado no caso da integral do seno, podemos afirmar que a operação de integração do cosseno é definida por:
Cuja constante C é a constante devido a indefinição no processo de antidiferenciação
Notas
[editar | editar código-fonte]- ↑ 1,0 1,1 Ver também no Wolfram Alpha
- ↑ Ver também no Wolfram Alpha
- ↑ Ver também no Wolfram Alpha
- ↑ Ver também no Wolfram Alpha
- ↑ Ver também no Wolfram Alpha
- ↑ Ver também no Wolfram Alpha
Trigonométricas II
[editar | editar código-fonte]Esta seção é a continuação do estudo trigonométrico, iniciado no capítulo anterior, que foi criada após o aumento progressivo do conteúdo.
Tangente e secante
[editar | editar código-fonte]Quando definimos o seno e o cosseno fizemos a referência a seu significado no ciclo trigonométrico, da mesma forma introduziremos a tangente neste momento. Como já vimos anteriormente a derivada é uma função que representa a declividade de uma curva, da mesma forma podemos definir a tangente, pois essencialmente, ela representa a declividade do ciclo para cada ângulo em particular, ou seja, se traçarmos uma reta orgononal a cada ponto do ciclo trigonométrico e relacionarmos ao ângulo que forma com o eixo x, teremos retas com declividades iguais às tangentes desses ângulos. Como cada ponto do ciclo é definido por e o valor inicial é sempre nulo, temos um valor de declividade tal que:
que é:
Desta forma também podemos concluir que a tangente é a representação do cateto oposto ao ângulo quando mantemos o cateto adjacente constante e unitário, cosiderando este ponto de vista, qual seria o valor da hipotenusa?
Para definir h, a hipotenusa, façamos :
Da identidade relacional temos:
portanto:
Este valor é o que chamamos de secante, que é outra função importante para o estudo trigonométrico, então podemos dizer que:
Nas próximas seções veremos que a secante mantém íntimas ralações com a tangente.
Identidades (2)
[editar | editar código-fonte]Como definimos as identidades entre seno e cosseno, incluiremos as identidades que incluem tangente e secante nesta seção, todas são algebricamente dedutíveis e intercambiaveis.
I-14 Relacionando tangente e secante
[editar | editar código-fonte]Seja x uma variável que expressa o ângulo em cada ponto do ciclo trigonométrico, entre podemos afirmar que:
Conforme visto nos conceitos iniciais logo acima, a relação é conseqüência direta das relações triangulares que definem as funções tangente e secante.
I-15 Tangente da diferença
[editar | editar código-fonte]Sendo a e b dois ângulos no ciclo trigonométrico:
Comprovação:
Considerando a definição da tangente temos:
Resultando em:
O que comprova a identidade.
I-16 Tangente da soma
[editar | editar código-fonte]
Comprovação:
Admitamos e teremos pela tangente da diferença:
Considerando que a tangente é:
E que o seno é determinante para o sinal enquanto o cosseno não é, concluímos que o sinal da tangente é igual ao da variável, tal qual se comporta o seno, logo:
O que comprova a identidade.
Derivada da tangente
[editar | editar código-fonte]Seja , uma função contínua em , visto que , o que nos obriga a excluí-lo do intervalo, podemos verificar que:
logo, pela derivada da razão:
Portanto:
Derivada da secante
[editar | editar código-fonte]Seja , uma função contínua em , visto que , o que nos obriga a excluí-lo do intervalo, podemos verificar que:
logo, pela derivada da razão:
O que nos revela:
Integral da tangente
[editar | editar código-fonte]Seja a função , definida contínua no intervalo onde seus valores estão sendo considerados, podemos deduzir que:
Por outro lado, se:
O que nos possibilita afirmar que:
Portanto:
Integral da secante
[editar | editar código-fonte]Seja a função , dizemos que sua integral é a função e podemos deduzí-la através de substituições algébricas como segue:
multiplicando e dividindo :
Por outro lado, se:
,
logo, por substituição, temos:
, sendo , o que nos permite fazer:
Portanto:
Cotangente e cossecante
[editar | editar código-fonte]Considerando a semelhança entre as definições das funções trigonométricas até aqui abordadas, observamos que para cada função, curiosamente há uma "co-função", assim como temos um seno e um "co-seno" temos uma tangente e uma "co-tangente". A função cotangente é definida tal qual a analogia adotada antes para seno e cosseno; podemos dizer que as funções estão relacionadas ao eixo y e as "co-funções" estão relacionadas ao eixo x, a imagem de um ponto no ciclo trigonométrico a partir do eixo x é o cosseno do ângulo e o seno é a imagem do mesmo ponto vista pelo eixo y. Para verificar essa relação observe o gráfico:
Figura 8
Se nós fizermos a mesma observação entre tangente e cotangente concluiremos que a tangente é a imagem deste ponto do ciclo trigonométrico no eixo paralelo ao eixo y traçado a partir da coordenada (1,0) e a cotangente é a sua "co-função" que espelha o ponto no eixo paralelo ao eixo x na coordenada (0,1). Segundo o mesmo critério de analogia podemos dizer que a função cossecante é o valor da hipotenusa do triângulo formado entre o raio unitário do ciclo e a cotangente relacionada a um ponto do ciclo, da mesma forma que a secante é o valor da hipotenusa do triângulo formado entre o raio unitário do ciclo e a tangente do mesmo ponto.
Podemos deduzir a fórmula de definição da função cotangente fazendo uma análise de semelhança de triângulos, notamos no ciclo que:
O que nos revela:
Da mesma forma podemos verificar uma relação de semelhança de triângulos para determinar a cossecante, vemos que existe a seguinte relação:
Que define a cossecante como:
Identidades (3)
[editar | editar código-fonte]Algumas identidades são conseqüentes das definições, apresentamos as mais usuais que poderão ser úteis nos demais capítulos deste livro, as identidades, de modo geral, são altamente intercambiáveis devido a natureza cíclica das funções trigonométricas, no nosso estudo abordamos as mais utilizadas.
Conseqüentes das definições:
Derivada da cotangente
[editar | editar código-fonte]Seja a função , considerando que:
Novamente usamos a regra da derivada da razão:
Portanto:
Derivada da cossecante
[editar | editar código-fonte]Seja a função , considerando que:
Novamente usamos a regra da derivada da razão:
Portanto:
Integral da cotangente
[editar | editar código-fonte]Seja a função , considerando que:
Sua integral é:
Sendo :
Logo:
E, por substituição:
Integral da cossecante
[editar | editar código-fonte]Seja a função ,
Sua integral é:
Sendo :
Podemos então multiplicar e dividir u na equação da integral anterior:
Logo:
E, por substituição:
Inversas das trigonométricas
[editar | editar código-fonte]O conjunto de equações até o momento abordadas nos trazem uma nova questão: Quais as funções que nos permitem encontrar o ângulo a partir do resultado de uma função trigonométrica?
A resposta está nas inversas das funções trigonométricas, também chamamos de arc-funções. Uma arc-função é uma função na qual podemos inserir o valor da função e encontrar o arco que originou este resultado, por isto dizemos que a é aquela que retorna o valor do arco cuja função resulta em x.
arcseno e arccosseno
[editar | editar código-fonte]Conforme o anteriormente exposto, temos que encontrar as funções que nos dão o valor do arco que forma um seno x e o arco que forma um cosseno x, para isto cabe uma observação:
- O seno e o cosseno podem ser resultado de vários ângulos diferentes, devido a característica cíclica que as mesmas apresentam quando assumimos valores em , portanto não existem as funções inversas do seno e cosseno neste intervalo.
O exposto nos obriga a limitar o intervalo do seno e do cosseno dentro de uma faixa que possibilite encontrar apenas um arco para cada valor, é necessário que escolhamos um intervalo onde as funções sejam monótonas. Considerando a função seno dentro da faixa: , podemos dizer que a condição de inversibilidade é satisfeita, da mesma forma a função cosseno dentro da faixa: também apresenta valores únicos para cada arco tomado.
Assim, dizemos que:
Da mesma forma que:
Derivadas do arcseno e arccosseno
[editar | editar código-fonte]Seja a função , sendo a sua inversa:
,
podemos operá-la desta forma:
,
Por outro lado:
O que nos dá:
,
Logo:
Ainda temos que a função , sendo a sua inversa:
,
podemos operá-la desta forma:
,
Por outro lado:
O que nos dá:
,
Logo:
Integrais do arcseno e arccosseno
[editar | editar código-fonte]Para integração das funções arcseno e arccosseno, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.
Arctangente e arccotangente
[editar | editar código-fonte]Definimos a função:
,
arctangente de x, como a inversa da função:
,
tangente de y, para todo o intervalo , porque no mesmo há apenas um valor de tangente para cada arco.
Do mesmo modo podemos definir a função:
,
arccotangente de t, como a inversa da função:
,
cotangente de z, para todo o intervalo , porque no mesmo há apenas um valor de cotangente para cada arco.
Derivadas da arctangente e arccotangente
[editar | editar código-fonte]Seja a função , sendo a sua inversa:
,
podemos operá-la desta forma:
,
Por outro lado:
O que nos dá:
,
Logo:
Ainda temos que a função , sendo a sua inversa:
.
Por outro lado:
O que nos dá:
,
Logo:
Integrais da arctangente e arccotangente
[editar | editar código-fonte]Para integração das funções arctangente e arccotangente, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.
Arcsecante e arccossecante
[editar | editar código-fonte]Definimos a função:
,
arcsecante de x, como a inversa da função:
,
secante de y, para os intervalos de x: , onde, nos mesmos, há apenas um valor de secante para cada arco.
A função é relacionada a função como segue:
Do mesmo modo podemos definir a função:
,
arccosecante de t, como a inversa da função:
,
cosecante de y, para os intervalos de x: , onde, nos mesmos, há apenas um valor de secante para cada arco.
A função é relacionada a função como segue:
Derivadas da arcsecante e arccossecante
[editar | editar código-fonte]Seja a função:
que tem correspondência em:
Sendo:
Portanto:
para
Integrais da arcsecante e arccossecante
[editar | editar código-fonte]Para integração das funções arcsecante e arccossecante, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.
Trigonométricas inversas como integrais algébricas
[editar | editar código-fonte]Como resultado das derivadas de funções trigonométricas inversas algumas integrais de funções algébricas podem ser convertidas em "arc-funções", são elas:
Em todas, como é de costume, encontramos a constante de antidiferenciação C.
hiperbólicas
[editar | editar código-fonte]A hipérbole é uma das funções cônicas exploradas em geometria analítica e tem como característica uma íntima relação com as exponenciais e , as funções desta seção são obtidas segundo o mesmo princípio das funções trigonométricas utilizando-se da hipérbole como função geratriz, ou seja, para cada ponto cartesiano de um gráfico da hipérbole podemos adotar a análise feita no ciclo trigonométrico, desta análise resultam as funções discutidas nesta seção.
As funções hiperbólicas são essencialmente exponenciais, portanto o seu estudo é simplificado nesta seção, visto que suas conseqüências são imediatamente dedutíveis pelos princípios já vistos na seção que trata de funções exponenciais.
Seno e cosseno hiperbólicos
[editar | editar código-fonte]A função seno hiperbólico é obtida a partir da hipérbole da mesma forma que o seno no ciclo trigonométrico, sua definição pode ser obtida por análise geométrica do gráfico da hipérbole , onde encontramos:
A função cosseno hiperbólico, que referenciamos ao cosseno no ciclo trigonométrico pode ser encontrado pela seguinte expressão:
Sendo obtida de forma similar a anterior.
O fato destas funções serem resultantes da soma e subtração de uma exponencial crescente e uma exponencial decrescente lhes conferem propriedades únicas, do mesmo modo temos a possibilidade de fazer analogias para uma fácil assimilação dos seus conceitos. Estas funções também são largamente úteis devido ao fato de serem comuns em problemas reais na física, na química e nas engenharias.
Relacionando seno e cosseno hiperbólico
[editar | editar código-fonte]Considere a operação: ,
Da definição temos:
logo:
Derivada do seno hiperbólico
[editar | editar código-fonte]Seja a função seno hiperbólico , podemos dizer que:
sendo:
Portanto:
Derivada do cosseno hiperbólico
[editar | editar código-fonte]Seja a função cosseno hiperbólico , podemos dizer que:
sendo:
Portanto:
Integral do seno hiperbólico
[editar | editar código-fonte]A integral do seno hiperbólico também é facilmente obtida pela definição:
Concluimos que:
Integral do cosseno hiperbólico
[editar | editar código-fonte]A integral do cosseno hiperbólico também é facilmente obtida pela definição:
Concluimos que:
Tangente e secante hiperbólicas
[editar | editar código-fonte]Da mesma forma que no caso trigonométrico a tangente e as outras funções hiperbólicas são definidas através do seno e do cosseno, ou seja, a tangente é definida como:
ou
A secante hiperbólica é definida como:
ou
Relacionando tangente e secante hiperbólicas
[editar | editar código-fonte]Vamos desenvolver a expressão abaixo:
Portanto:
Derivada da tangente hiperbólica
[editar | editar código-fonte]Seja a função , temos:
Portanto:
Derivada da secante hiperbólica
[editar | editar código-fonte]Seja a função , temos:
e finalmente:
Integral da tangente hiperbólica
[editar | editar código-fonte]Seja a função , temos:
Se fizermos:
verificamos:
e finalmente:
Integral da secante hiperbólica
[editar | editar código-fonte]Para integração da função secante hiperbólica, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.
Cotangente e cossecante hiperbólicas
[editar | editar código-fonte]A cotangente hiperbólica é definida como:
ou
A cosecante hiperbólica é definida como:
ou
Relacionando cotangente e cossecante hiperbólicas
[editar | editar código-fonte]Vamos desenvolver a expressão abaixo:
Portanto:
Derivada da cotangente hiperbólica
[editar | editar código-fonte]Seja a função , temos:
Portanto:
Derivada da cossecante hiperbólica
[editar | editar código-fonte]Seja a função , temos:
e finalmente:
Integral da cotangente hiperbólica
[editar | editar código-fonte]Seja a função , temos:
Se fizermos:
verificamos:
e finalmente:
Integral da cossecante hiperbólica
[editar | editar código-fonte]Para integração da função cossecante hiperbólica, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.
Inversas das hiperbólicas
[editar | editar código-fonte]As funções hiperbólicas inversas são particularmente interessantes, elas estão ligadas ao logaritmo natural e por este motivo, sua análise é excencialmente exponencial, como a análise das funções hiperbólicas, deste fato nascem novas possibilidades para lidar com problemas relacionados a análises de estruturas não lineares.
Análise da inversão das variáveis
[editar | editar código-fonte]As funções hiperbólicas são característicamente analisadas de forma semelhante às trigonométricas, o que nos sugere a análise da inversão das variáveis das equações hiperbólicas da forma:
,
Para a forma:
Isto é particularmente fácil de implementar para funções do tipo , que são funções monótonas e contínuas, para as demais que restringem sua continuidade em um determinado intervalo, devemos adotar faixas para o domínio de cada uma em particular.
É importante notar que, embora as funções hiperbólicas sejam semelhantes às trigonométricas, estas funções se baseiam em ângulos que devem ser analisados de forma diferente dos trigonométricos, lembre-se que o raio de uma função circular é constante, o que não acotece com uma função baseada em uma cônica, neste caso a hipérbole, por isso escolhemos a nomeclatura de argfunch(x), pois não podemos classificar os ângulos hiperbólicos como arcos.
argsenh e argcosenh
[editar | editar código-fonte]Agora consideremos a função , então:
Podemos fazer , logo:
O que resulta na equação:
cujas raízes são:
Podemos apenas admitir: , consequentemente:
Substituindo as variáveis x por y e t por x, temos a inversa de que é:
No caso de , a dedução é similar:
Podemos fazer , logo:
O que resulta na equação:
cujas raízes são:
Podemos apenas admitir: , consequentemente:
Substituindo as variáveis x por y e t por x, temos a inversa de que é:
,
Derivadas de argsenh(x) e argcosh(x)
[editar | editar código-fonte]Considerando as fórmulas deduzidas acima, temos:
de onde deduzimos:
resultando:
E para
de onde deduzimos:
e finalmente:
,
Integrais de argsenh(x) e argcosh(x)
[editar | editar código-fonte]As integrais destas funções precisam de um tratamento diferenciado, utilizando-se os métodos do próximo capítulo: Técnicas de integração, proponho que o leitor as faça como exercício do mesmo.
argtgh e argsech
[editar | editar código-fonte]Considerando , temos:
se :
o que resulta na equação:
cujas raízes são:
Onde apenas podemos admitir e :
Substituindo x por y e t por x:
Que é a inversa da , portanto:
,
Ou,
,
Considerando , temos:
se :
o que resulta na equação:
Cujas raízes são:
Onde apenas podemos admitir e :
Substituindo x por y e t por x:
Que é a inversa da , portanto:
,
Derivadas de argtgh e argsech
[editar | editar código-fonte]Seja ,
Deduzimos que sua derivada é:
Que, depois de submetida à regra da cadeia e da razão, se torna:
e, finalmente:
,
Note que, devido à limitação do domínio imposto pela variável na função primitiva, a derivada herda a mesma limitação, uma vez que a função não existe fora deste domínio.
Seja ,
Deduzimos que sua derivada é:
Que, depois de submetida à regra da cadeia e da razão, se torna:
e, finalmente:
Integrais de argtgh e argsech
[editar | editar código-fonte]As integrais destas funções precisam de um tratamento diferenciado, utilizando-se os métodos do próximo capítulo: Técnicas de integração, proponho que o leitor as faça como exercício do mesmo.
argcotgh e argcosech
[editar | editar código-fonte]Considerando , temos:
se :
o que resulta na equação:
cujas raízes são:
Onde apenas podemos admitir e :
Substituindo x por y e t por x:
Que é a inversa da , portanto:
,
Ou,
,
Considerando , temos:
se :
o que resulta na equação:
Cujas raízes são:
Onde apenas podemos admitir :
Substituindo x por y e t por x:
Que é a inversa da , portanto:
Derivadas de argcotgh e argcosech
[editar | editar código-fonte]Seja ,
Deduzimos que sua derivada é:
Que, depois de submetida à regra da cadeia e da razão, se torna:
e, finalmente:
,
Note que, devido à limitação do domínio imposto pela variável na função primitiva, a derivada herda a mesma limitação, uma vez que a função não exite fora deste domínio.
Seja ,
Deduzimos que sua derivada é:
Que, depois de submetida à regra da cadeia e da razão, se torna:
e, finalmente:
,
Integrais de argcotgh e argcosech
[editar | editar código-fonte]As integrais destas funções precisam de um tratamento diferenciado, utilizando-se os métodos do próximo capítulo: Técnicas de integração, proponho que o leitor as faça como exercício do mesmo.
Considerações iniciais
[editar | editar código-fonte]A integração é um processo que demanda certa habilidade e técnica, ele provê um meio indispensável para análises de cálculos diversos, além disso o meio de integrar certas funções deve ser exercitado até que sejamos capazes de absorver a sua essência. O problema da integração deve ser visto como uma análise que pode conduzir a resultados algébricos diversos, quando tomadas técnicas diversas, que concordam, porém, em resultado numérico.
Devido à necessidade de exercício dessas técnicas que apresentaremos, teremos mais exemplos neste capítulo, uma ótima maneira de introduzir o conteúdo enquanto a teoria é exposta. A natureza diversa das formas de integrais nos obriga a fazer este estudo a parte, pois certas funções são peculiarmente difíceis de serem analisadas antes da utilização de algum artifício que permita sua simplificação, este é o objetivo deste capítulo: trazer ao leitor os processos de integração e as diversas possibilidades de simplificação de funções para a aplicação destes processos.
Por partes
[editar | editar código-fonte]A técnica de integração por partes consiste da utilização do conceito de diferencial inversa aplicado à fórmula da regra da diferencial do produto, ou seja:
Que após a antidiferencial se torna:
E, portanto:
A utilização desta fórmula para melhorar o processo de integração implica na necessidade de uma breve explanação, o processo consiste em observar a função a ser integrada como sendo uma integral , ou seja, devemos separar a função em duas partes: uma, chamamos de u, que consideraremos função primitiva e outra dv que será uma diferencial, desta forma, faremos a integração da parte dv para encontrar v e depois subtrairemos a integral da mesma com relação a diferncial de u: du. Parece um tanto incomun a princípio, porém após o hábito no uso da técnica, esta se torna muito útil.
Outro fato deve ser explorado: como o processo demanda a integração da diferencial dv nos vem a questão sobre a necessidade de utilização da constante de antidiferenciação C, portanto façamos a verificação da fórmula utilizando-a:
Se ,
Ou seja, a constante é dispensável para o cálculo da integral que resulta em v.
Exemplo 1 - Caso do logaritmo
[editar | editar código-fonte]Utilização da integração por partes na resolução da integral do logaritmo natural:
Separamos a diferencial dx e a primitiva , procedendo as operações inversas:
depois:
Aplicando à fórmula de integração por partes:
Também há os que preferem simplificar mais, desta forma:
Sendo C a constante de antidiferenciação.
Exemplo 2 - Caso do arcseno
[editar | editar código-fonte]Utilização da integração por partes para encontrar a integral do arcseno:
Separamos as partes e operamos para encontrar as respectivas inversas:
Assim:
Aplicando à fórmula da integração por partes:
agora consideremos o seguinte:
logo:
Portanto:
Sendo C a nossa tradicional constante de antidiferenciação.
Exemplo 3 - Caso do arccosseno
[editar | editar código-fonte]Utilização da integração por partes para encontrar a integral do arccosseno:
Separamos as partes e operamos para encontrar as respectivas inversas:
depois:
Aplicando à fórmula da integração por partes:
agora consideremos o seguinte:
logo:
Portanto:
Sendo C a nossa tradicional constante de antidiferenciação.
Exemplo 4 - Caso do arctangente
[editar | editar código-fonte]Utilizando a integração por partes para encontrar a integral do arctangente:
Separando as partes e operando as inversas:
e
Aplicamos a fórmula da integração por partes:
Por outro lado:
onde podemos extrair:
voltando ao desenvolvimento da integral:
Portanto:
Novamente, temos C como contante de antidiferenciação.
Exemplo 5 - Algébricas com exponenciais
[editar | editar código-fonte]Este é um exemplo que nos revela uma função claramente divisível em duas partes:
Considerando as partes:
e:
Substituindo na fórmula de integração por partes:
O segundo lado desta expressão pode ser novamente simplificado, aplicando a integração por partes mais uma vez:
Portanto:
Exemplo 6 - Secante com expoente maior que 2
[editar | editar código-fonte]Utilizando a integração por partes para resolução da integral de secantes com expoente maior que 2:
Podemos fazer:
E aplicar a integração por partes:
E finalmente:
Com C constante.
Por substituição trigonomética
[editar | editar código-fonte]A existência de relações algébricas que nos levam a arcos nos traz a possibilidade de converter uma expressão algébrica, conseqüentemente uma função algébrica, em uma função trigonométrica. A possibilidade de lidar com certas funções de forma trigonométrica nos leva à utilizar os artifícios das identidades para a simplificação dessas.
Transformando expressões algébricas em trigonométricas
[editar | editar código-fonte]Três funções algébricas têm semelhanças com funções trigonométricas que são notoriamente úteis para a simplificação de algumas funções, elas são:
Sendo "a" constante.
Note que as expressões são meramente relações quadráticas que descendem da relação quadrática entre todos os lados de um mesmo triângulo: , se escolhermos um par (variável,constante) e substituirmos na equação teremos as expressões acima como resultantes, teremos uma variável dependente para cada par (variável,constante), por exemplo: se fizermos , e teremos a expressão (2) como resultante (y).
Imagine que temos uma nova variável e que:
Sendo:
Podemos dizer que:
Portanto:
quando e
O exposto acima encontra respaudo no fato de que a expressão é simplesmente a tradução da relação métrica de um triângulo retângulo para definição do cosseno a partir do seno, como segue:
Se fizermos a comparação entre as funções e o gráfico acima, substituindo as variáveis e constantes de acordo com a função dada, teremos o seguinte:
- Na função é uma tangente;
- Na função é um seno;
- Na função é uma secante.
O que nos dá as substituições:
| Expressão | Substituição |
A substituição trigonométrica na integração
[editar | editar código-fonte]Agora, considere o fato de que a função tem como integral a função , então podemos fazer:
Uma vez, que pela análise anterior já sabemos que quando fazemos temos:
então:
Temos que encontrar :
O que nos revela algo interessante:
Ou seja:
Logo:
Exemplo 7 - Substituição por seno
[editar | editar código-fonte]Seja a função: , calculemos a sua integral por substituição trigonométrica:
Fazendo a transformação de variáveis:
A integral será:
Como:
Portanto:
Sendo C a constante de antidiferenciação.
Exemplo 8 - Substituição por secante
[editar | editar código-fonte]Seja a função: , calculemos a sua integral por substituição trigonométrica:
Se
Introduzimos a variável angular , de forma que:
e sua diferencial:
Substituindo na equação anterior:
Retornando a função ao domínio da variável x:
Portanto:
Sendo C a constante de antidiferenciação.
Exemplo 9 - Substituição por tangente
[editar | editar código-fonte]Seja a função: , calculemos a sua integral por substituição trigonométrica:
Se
Introduzimos a variável angular , de forma que:
e sua diferencial:
Substituindo na equação anterior:
Retornando a função ao domínio da variável x:
Portanto:
Sendo C a constante de antidiferenciação.
Funções racionais com denominadores lineares
[editar | editar código-fonte]Denominadores de segundo grau ou mais são um pouco mais problemáticos quando queremos definir uma integral, por exemplo:
Seja a função:
É possível demonstrar que a função pode ser fatorada da seguinte forma:
Onde A e B são os fatores a serem definidos; o processo para definí-los será explicado mais adiante e são as raízes da equação formada a partir do denominador quando o igualamos a zero.
Porém a demonstração disto está fora do escopo deste livro, deve ser tratado na algebra avançada.
Em todo caso, o teorema é bastante útil para a simplificação de tais funções.
Conceito da fatoração de funções racionais polinomiais
[editar | editar código-fonte]As funções racionais do formato: têm uma característica bem interessante, os seus denominadores , quando fatorados em partes lineares e quadráticas permitem que possamos escrever a referida função como uma soma:
Seja a função , podemos simplificá-la desta forma:
Considerando as raízes da equação , podemos dizer que:
Os fatores são calculados fazendo:
logo, as raízes permitem: , então temos que admitir que ao analisar cada raiz:
Quando :
Quando :
então, podemos fazer:
A simplificação de denominadores usada na integração
[editar | editar código-fonte]O artifício de encontrar componentes lineares para substituir os denominadores, como exposto no tópico anterior, permite uma boa simplificação de integrais com denominadores polinomiais de graus superiores, porém ainda depende da determinação das raízes do polinômio dos denominadores, o que limita a nossa capacidade de resolução aos polinômios biquadráticos. Sem levar em conta este fato, podemos simplificar a integral para uma boa parcela de problemas que apresentam estes formatos de expressões.
Vejamos o caso anterior:
A função:
,
pode ser substituída por:
O que nos permite fazer:
Com C Constante.
Exemplo 10 - Decomposição do denominador em fatores lineares
[editar | editar código-fonte]Utilizando a decomposição de funções racionais em funções de denominadores lineares para a simplificação de integrais.
Seja a função:
Encontremos a integral:
Devemos simplificar a função, para isto podemos efetuar a divisão polinomial, que resulta:
Ainda resta uma parte fracionária que podemos decompor usando o método que já vimos neste capítulo:
As raízes nos revelam que:
logo podemos fazer:
ou
Analisando os valores da equação quando x se iguala as raízes:
Para :
Para :
Podemos concluir que:
Desta forma temos a função simplificada:
Podemos integrá-la:
Portanto:
Sendo C a constante de antidiferenciação.
Funções racionais com denominadores quadráticos
[editar | editar código-fonte]A segunda categoria de funções racionais às quais temos que nos aplicar são as que dão origem a denominadores quadráticos.
Decompondo funções racionais em denominadores quadráticos
[editar | editar código-fonte]Quando não temos como encontrar as raízes de certos denominadores quadráticos podemos mantê-los e utilizar a seguinte substituição:
O teorema que estabelece esta relação faz parte da álgebra avançada, portanto não entraremos em detalhe neste livro, porém faremos uso de suas consequências como forma de simplificação, como fizemos com a decomposição de denominadores em fatores lineares vista na seção anterior.
A melhor maneira de definir a parte é substituir a variável x nesta fazendo-a igual a derivada do denominador, ou seja:
No lado esquerdo da equação acima, se houver variáveis de expoente maior que o maior expoente do lado direito devemos proceder uma simplificação efetuando a divisão dos polinômios, caso contrário teríamos:
Separamos cada fator de acordo com o grau da variável, obtendo:
Para
Para
logo:
e
Porém em funções racionais mais comuns temos que lidar com funções com partes lineares e quadráticas, onde o processo de encontrar os valores para depende das outras partes envolvidas, para verificar o processo, vejamos o próximo exemplo...
Exemplo 11 - Decomposição de funções racionais em denominadores quadráticos e lineares
[editar | editar código-fonte]Utilizando a decomposição de funções racionais com denominadores quadráticos para simplificar o cálculo da integral.
Seja a função:
Calculemos a sua integral indefinida:
Antes de tudo façamos a simplificação dos polinômios, primeiro faremos a divisão simples do numerador pelo denominador:
Da divisão separamos a parte do resto:
Procedendo a decomposição dos fatores:
Que nos permite fazer:
Quando separamos os fatores para cada variável de expoente correspondente em ambos os lados da equação, temos:
Resolvendo o sistema linear temos:
Podemos escrever a função como:
Agora podemos integrá-la:
Numa conclusão imediata podemos dizer que:
Porém em estudos onde se exige um tratamento mais algébrico com exponenciais e logaritmos, podemos adotar um formato como este:
Portanto:
Com C constante.
Por substituição hiperbólica
[editar | editar código-fonte]Se podemos fazer substituições trigonométricas em funções algébricas e existem funções hiperbólicas, por que não utilizar o mesmo método de substituição com funções hiperbólicas? Temos mais esta possibilidade para simplificar a integração de funções algébricas; Detalharemos nesta seção as formas de substituição com funções hiperbólicas, que podem ser uma valorosa ferramenta para a integração de funções mais complexas.
Integrais resultantes das hiperbólicas inversas
[editar | editar código-fonte]Como conseqüência das derivadas de funções hiperbólicas inversas, temos as seguintes integrais:
| Função: | Derivada: | Integral relacionada: |
| , | ||
| , | ||
| , | ||
| , | ||
| , |
Transformando funções algébricas em hiberbólicas
[editar | editar código-fonte]A técnica aqui exposta é semelhante à abordada na seção Transformando expressões algébricas em trigonométricas, a diferença básica está nas expressões a serem substituídas, uma vez que as identidades trigonométricas e hiperbólicas são sutilmente distintas, as expressões seguem a mesma tendência. Então vamos ver quais são as correspondentes algébricas para as funções hiperbólicas:
- Na função é um seno hiperbólico;
- Na função é uma tangente hiperbólica;
- Na função é uma cotangente hiperbólica.
O que nos dá as substituições:
| Expressão | Substituição |
Em todas as substituições consideramos um triângulo retângulo cujo vértice relacionado ao ângulo faz parte de uma perspectiva hiperbólica, ou seja, o ângulo está em , trata-se de uma abstração que pode ser comprovada em cálculo avançado, o nosso objetivo aqui é de fornecer as ferramentas necessárias para análises desse tipo.
A substituição hiberbólica na integração
[editar | editar código-fonte]Considere a função: e que sua integral seja: , então teremos:
Concebemos uma nova variável de forma que:
conseqüentemente, sua diferencial é:
Substituindo na equação inicial, temos:
Ou seja:
Porém, devido a natureza exponencial das funções hiperbólicas inversas, ainda podemos transformar esta equação na forma puramente logarítmica:
Finalmente:
Funções racionais trigonométricas
[editar | editar código-fonte]O problema da integração de funções racionais trigonométrica consiste, basicamente, na característica da complexibilização progressiva quando estas funções são submetidas às técnicas convencionais de substituição, no momento que tentamos substituir a expressão original temos que definir sua diferencial, o que implica na criação de mais um termo a ser incorporado a expressão original.
Digamos que tenhamos que integrar a função:
Ao adotarmos a linha tradicional de substituições teremos:
e
no entanto:
logo teremos que integrar:
de forma que:
Que, pelo menos, é uma função algébrica pura, mas que ainda demanda um certo trabalho para ser integrada... Portanto concluimos que o processo de substituição de variáveis e diferenciais não ajuda muito.
Nesta seção exporemos um método de substituição mais eficiente para estes casos.
Usando as identidades trigonométricas
[editar | editar código-fonte]Apresentamos duas identidades que serão muito úteis para a simplifição de funções racionais trigonométricas, são elas:
- Seno em forma algébrica
- Cosseno em forma algébrica
Basicamente são resultantes de um processo de substituição mais bem estruturado, para possibilitar a simplificação da integração.
I-17 Cosseno em forma algébrica
[editar | editar código-fonte]A identidade relacionada ao Cosseno é apresentada antes da relacionada ao seno pois será útil para a sua dedução.
Considere a seguinte definição:
logo, é dedutível que:
- Demonstração:
Considerando a identidade I-2 Cosseno da soma, temos, por conseqüência:
Se :
ou
Por outro lado:
Substituindo na identidade temos:
que nos dá:
I-18 Seno em forma algébrica
[editar | editar código-fonte]Ainda considerando a definição:
também é dedutível que:
- Demonstração:
Da identidade anterior:
Da I-1 Identidade relacional básica:
Fazendo as substituições:
logo:
Integrando
[editar | editar código-fonte]Temos duas funções trigonométricas fundamentais na forma algébrica para substituir as originais na forma trigonométrica, porém para integrar as funções racionais substituindo-as por estas temos que encontrar uma diferencial correspondente para esta nova variável algébrica que criamos.
Da definição inicial:
Diferenciando:
Da identidade I-14 Relacionando tangente e secante:
de onde concluimos que:
Agora podemos encontrar a integral proposta no início da seção:
para , temos:
ou seja:
Não é incrível? !!!
e
Jamais poderemos nos esquecer de C, a famigerada constante de antidiferenciação que tanto nos persegue.
Tabela de integrais
[editar | editar código-fonte]Para auxiliar nos cálculos, consulte a tabela de integrais na wikipédia
Indeterminação
[editar | editar código-fonte]Nos deparamos constantemente com situações onde é necessário que algum grau de indeterminação seja considerado e analisado, na matemática elementar temos as formas indeterminadas que por séculos intrigou matemáticos e filósofos famosos, uma das mais comuns é a raiz , porém lidar com esta indefinição em matemática elementar já sabemos, um estudo sobre números complexos será aplicado ao Cálculo nos livros subseqüentes. Para o presente estudo faremos a análise do cálculo em funções que geram valores indefinidos, mas que podem ser reavaliados por um limite infinitesimal. O artifício de analisar a função sob um limite pode nos revelar resultados bastante conclusivos, que podem sanar boa parte dos problemas que encontramos no uso do cálculo.
Que esteja bem claro que a análise dos valores aqui sugerida não traz um argumento definitivo para a indeterminação, apenas traz meios capazes de solucionar questões que passam pela indeterminação, mas que podem ser solucionados quando as tendências são suficientes para uma conclusão a respeito do problema dependente e não da indeterminação em si.
Formas indeterminadas
[editar | editar código-fonte]Basicamente analisaremos as formas indeterminadas geradas pelo denominador nulo, das quais destacamos os seguintes casos:
- Forma
- Forma
- Forma
Ainda temos:
- Forma
- Forma
Na maioria dos casos temos a indeterminação em um ponto do domínio, onde o valor de um denominador é nulo para uma determinada função, desta forma podemos definir a razão como uma função composta da seguinte forma:
De onde podemos fazer as seguintes considerações:
Dado um ponto onde:
Podemos dizer que apresenta uma forma indeterminada em , porém o limite: pode ser determinado. Podemos fazer:
A segunda forma de indeterminação acontece quando, dado um ponto , onde:
Na terceira forma de indeterminação acontece quando, dado um ponto , onde:
T42 - Valor médio de Cauchy
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função numerador e a função denominador em uma relação, então há pelo menos um valor no intervalo no qual esta relação é definida por: | ||
Demonstração
Considere que em dois extremos (máximos ou mínimos) do intervalo tenhamos pontos definidos em ambas as funções, então poderemos traçar uma reta para cada par de extremos em cada função no intervalo. Assim, temos duas retas que nos possibilitam afirmar que, definidos apropriadamente os pontos que determinam as retas, há pelo menos um ponto de cada função neste intervalo com derivada igual a inclinação destas retas, por outro lado podemos criar condições para que a relação destas retas obedeçam as condições do teorema de Rolle e conseqüentemente o teorema do valor médio para derivadas, uma nova função que traz esta possibilidade é esta:
onde:
Define-se tal função pois:
Fato que torna válida a aplicação do teorema de Rolle.
derivando a equação:
Desta forma teremos pelo menos um ponto no intervalo onde a derivada: é nula,
Comentário:Observe que a demonstração acima poderia ter sido feita definindo-se como qualquer função da forma , sendo uma constante qualquer, tal constante não iria interferir na derivação e a validade das equações seriam mantidas pois o teorema de Rolle é valido não apenas para extremos onde , contanto simplesmente que (CM)
T43 - Regra de L'Hôpital
[editar | editar código-fonte]
| ||
|---|---|---|
| Dada a função:
indefinida em , é possível provar que: | ||
|
|
Demonstração do caso 1
[editar | editar código-fonte]Se
Temos do Teorema do valor médio de Cauchy:
Note que podemos fazer :
Uma vez que temos . observamos que:
e
sendo conforme definimos,
se reduz a:
Porém, se
Então
Daí pois está no intervalo Logo:
Portanto:
Demonstração do caso 2
[editar | editar código-fonte]Se quando ,
Uma vez que desejamos encontrar:
Podemos promover uma mudança de variável, ou seja, se o limite acima leva as funções a se anularem no infinito, então podemos fazer:
,
Desenvolvendo através da regra da cadeia temos:
O que torna o limite independente da mudança da variável.
Apresentação do caso 3
[editar | editar código-fonte]Embora não seja apropriado para este estudo de "Cálculo I" a demonstração da regra para casos onde temos as indeterminações do tipo:
,
A mesma regra também é válida, desde que as derivadas do numerador e do denominador não sejam nem nulas nem infinitas.
Integrais impróprias
[editar | editar código-fonte]Até agora lidamos com integrais definidas com limites de integração determinados, neste momento introduziremos os casos onde os limites de integração são indefinidos, mais específicamente quando estes limites tendem a infinitos ou valores nulos que geram infinitos na função a ser integrada. Embora grande parte das funções tenham valores indefinidos quando integrados com limites infinitos, uma boa parte fornece valores derinidos nestas situações, agora definimos a Integral imprópria como seque:
Todos os casos acima são integrais impróprias onde o valor pode se mostrar definido mesmo se os limites de integração não sejam total ou parcialmente definidos...
Há também a forma imprópria das integrais que fazem a função se tornar indefinida no ponto do limite de integração, ou seja:
De forma que se os limites existem é possível que a integral possa ser definida.
Limites infinitos
[editar | editar código-fonte]No caso em que os limites de integração se estendem a valores infinitos e que existe o limite da função para estes valores dizemos que a integral e que quando a função não apresenta definição para o limite dizemos que esta , ou seja chamamos as integrais impróprias de ou de acordo com a possibilidade ou não da definição do limite que permite calcular o referido valor da integral.
Para esta abordagem podemos verificar que, se é a integral indefinida de , podemos estabelecer que quando:
,
podemos fazer o limite da função, o que nos revela:
Desta forma podemos adotar o método de eliminação dos coeficientes nulos no infinito, usados para o caso de cálculo de limites no infinito, ou seja:
- Calcula-se a integral indefinida da função;
- Fatora-se a função para encontrar os maiores expoentes;
- Simplifica-se a mesma;
- E aplica-se o limite no infinito para cada valor de limite de integração quando usamos o Teorema fundamental do cálculo.
Limites nulos
[editar | editar código-fonte]Para os casos onde o cálculo da integral definida em limites de integração nulos conduz a valores indefinidos a regra é semelhante à anterior;
Seja as integrais definidas:
Sendo a integral indefinida:
Se:
Podemos calcular a integral definida fazendo:
T44 - Fórmula de Taylor
[editar | editar código-fonte]
| ||
|---|---|---|
| Seja a função diferenciável no intervalo , é possível demonstrar que: | ||
Onde é chamado de abscissa do valor médio da derivada , quando intui-se que quanto maior a ordem da derivada maior a quantidade de parcelas na equação e maior será a precisão da síntese da função através do polinômio.
Neste caso podemos dizer que o último termo da equação é o resto, dizemos que há convergência, o que torna a síntese possível, quando o resto diminui consecutivamente tendendo a zero, o que nos permite dizer que quanto menor o seu valor mais precisa a síntese da função.
Demonstração:
A função pode ser expressa, segundo o teorema fundamental do cálculo como:
Podemos separar a integral não resolvida da equação fazendo:
Se calcularmos a integral acima aplicando a integração por partes, teremos:
logo:
Fazendo esta substituição sucessivamente obtemos a fórmula de Taylor facilmente, façamos mais um passo para que se evidencie com mais clareza:
O que nos dá:
A evolução da equação é notória e por indução de integrações temos a referida fórmula.
Podemos definir o resto desta forma:
A integração na prática
[editar | editar código-fonte]Neste capítulo finalizamos o primeiro livro desta série do estudo do Cálculo, teremos agora a noção da quase infinita gama de utilizações que podemos fazer com a integração, que é uma das ferramentas de estudo algébrico e numérico mais frutíferas dentro da matemática, a integração fornece meios de calcular e avaliar diversos problemas complexos. Das aplicações da integração teremos uma amostra das mais obviamente concebíveis, iniciaremos o estudo de áreas em superfícies planas delimitadas por curvas, depois calcularemos volumes de objetos curvos, determinar a pressão que um líquido exerce sobre objetos curvos nele mergulhados e poderemos também, calcular comprimentos de curvas definidas for funções em um gráfico de coordenadas cartesianas.
Áreas
[editar | editar código-fonte]Talvez esta seja a mais óbvia aplicação para o cálculo de integrais, mas faremos algumas considerações sobre o estudo de áreas sob curvas que são importantes para que sejam evitados erros durante o processo de análise dos valores.
Como conseqüência direta da definição da integral temos a área sob da curva a ser integrada e o eixo das abscissas , seja a função , considerando que a mesma pode assumir valores tanto positivos como negativos, o fato de este sinal ser determinante para o processo de somatórias consecutivas, próprio da integral definida, devemos considerar no cálculo a possibilidade da diminuição de valores no caso de haver áreas com valores negativos.
Sinais
[editar | editar código-fonte]Da definição da integral de Riemann temos:
Obviamente, pode ser estabelecido e pode ser tomado como positivo se fizermos , logo nos resta:
Que é arbitrário pois depende da função , o que nos leva a concluir que o sinal da função determina o sinal da integral, ou seja, embora o módulo da integral represente a área delimitada pela curva e o eixo das abscissas, o seu valor relativo pode não expressar apenas valores positivos, o que nos indica que temos que analisar o sinal da função antes de calcular qualquer área através da integração.
Calculando as áreas
[editar | editar código-fonte]Consideremos o caso da função:
Os valores do seno entre e são positivos e entre e são negativos! Isto causa uma situação interessante, uma vez que as áreas entre a curva e o eixo dos dois intervalos, quando observadas no plano cartesiano, são identicas, a área das duas deveria ser o dobro de uma delas, entretanto a integral calculada no intervalo entre e é nula! Esta é a razão pela qual devemos fazer o módulo das integrais em cada intevalo de mudança de sinal, para que os valores das áreas nestes intervalos não se subtraiam, provocando erro no cálculo.
Devemos verificar os intervalos onde a função se torna negativa e inverter o sinal antes de efetuar a soma de áreas em cada intervalo, assegurando assim o correto valor do total de unidades quadradas de área, delimitadas pela curva e o eixo .
No caso da função acima, teremos:
Sob diversas situações devemos verificar o comportamento do gráfico, para que possamos determinar a melhor maneira de calcular a área, no caso de áreas delimitadas por duas curvas podemos determinar a área de cada curva em relação ao eixo e verificar o comportamento das curvas no gráfico para determinar a forma de calcular. Na seção subseqüente veremos como determinar a área delimitada por duas curvas.
Exemplo 1
[editar | editar código-fonte]Sejam duas funções:
Vamos calcular a área da região delimitada pelas curvas entre as suas interseções. O gráfico abaixo representa as funções e a área que desejamos calcular, a qual chamamos de A:

Inicialmente verifiquemos os pontos onde as funções se encontram, ou seja, os pontos onde :
Se
Se em ambas as funções .
Condições que nos revela o intervalo entre:
e
Obviamente devemos proceder a subtração entre a área delimitada pela reta e a área delimitada pela parábola, no caso da reta poderíamos ainda fazer a área do triângulo formado pela mesma e o eixo das abscissas, porém façamos todo o processo utilizando integração para que possamos ter um processo universal para o cálculo de áreas desse tipo.
Calculemos as integrais:
e
A área que queremos encontrar é:
logo:
unidades quadradas.
Volumes
[editar | editar código-fonte]Considerando as diversas formas que encontramos na natureza, podemos verificar que muito poucas têm formas regulares, dificilmente poderíamos encontrar o volume de um corpo sólido encontrado comumente na natureza por meio da geometria euclidiana, as curvas são comuns no nosso mundo, muitas delas podem ser determinadas por equações, porém antes que a teoria do Cálculo fosse elaborada os volumes eram calculados por aproximações. Hoje podemos obter muitos dos volumes de corpos sinuosos pelo Cálculo, os métodos descritos a seguir são os mais básicos para curvas que podem ser determinadas matematicamente, no decorrer dos próximos volumes aprenderemos a calcular formas mais complexas. Por hora, os cálculos que aqui serão apresentados já fornecem uma gama de aplicações bem ampla no nosso mundo onde a indústria usa cada vez mais curvas em seus produtos, obviamente teremos curvas matematicamente determináveis para estes casos, uma vez que o homem geralmente usa métodos de computação para criar seus produtos hoje em dia.
Curvas rotacionadas
[editar | editar código-fonte]Imaginemos que tenhamos uma curva matematicamente determinável, uma parábola, por exemplo, e tenhamos a área delimitada pela mesma e o eixo x, se fizermos com que o eixo y servisse de mastro e girassemos a parábola em torno do mesmo, o que teríamos? Teríamos um sólido formado pelas infinitas lâminas em forma de parábola.
| O efeito da rotação de uma parabola pode ser visualizada pelo gráfico tridimensional, o que vemos é o que chamados de parabolóide, um sólido semelhante ao recipiente de líquido de uma taça. Considerando a parte interna preenchida teremos um volume a ser calculado, o que podemos fazer utilizando o "Cálculo". |  |
| O efeito da rotação de uma elipse pode ser visualizada da mesma forma, o que nos possibilita ver o que chamados de elipsóide, um sólido semelhante a um ovo de réptil. O volume a ser calculado também pode ser conseguido através do "Cálculo". |  |
Sólidos delimitados por uma curva
[editar | editar código-fonte]O método para cálculo de volumes delimitados por curvas rotacionadas, como expostas acima, consiste na divisão do sólido em discos com raio igual ao valor da função que está sendo rotacionada, ou seja, para cada ponto da função teremos um disco de raio determinado pela mesma, o que nos permite fazer uma somatória de discos que acompanham o contorno da curva, vejamos o desenho abaixo:

Temos a função variando ao longo do eixo x, o que nos permite dizer que uma reta perpendicular ao eixo que passa por um ponto do gráfico é um raio de um disco... Em um intervalo onde , no qual , agrupemos pares de valores nas abscissas, de forma que o valor médio da função seja . Tomando cada disco com um volume aproximado de:
Considerando que a precisão do cálculo aumenta quando os discos se tornam menos espessos, temos que admitir que existe uma norma de partição que pode ser definida para o intervalo que pretendemos calcular, portanto podemos fazer:
Onde temos um volume de disco para cada ponto da curva e a norma pode ser inversamente proporcional ao número n. Logo, verificamos que:
ou
O intervalo refere-se a uma parte do sólido, da qual queremos calcular o volume.
Exemplo 2
[editar | editar código-fonte]Calcular o volume do sólido de revolução criado pela rotação da parábola em torno do eixo das abscissas, no intervalo .
Aplicando a fórmula anteriormente vista temos:
O volume é:
unidades cúbicas.
Sólidos delimitados por duas curvas
[editar | editar código-fonte]Agora podemos definir um sólido "oco", ou seja, para que um sólido tenha uma abertura devemos delimitar uma face externa e outra interna, o que nos pede que tenhamos uma curva para cada face.
Para a determinação das duas faces considere as duas funções e sendo que, para determinar o sólido de forma regular, estabelecemos o seguinte conjunto de regras:
Observemos a ilustração a seguir:

Consideremos um corte que nos permita observar uma fatia do sólido, como podemos ver o retângulo que tomamos no centro do desenho representa uma fatia de um disco "oco".
Agora podemos encontrar o volume ocupado pelo sólido, no espaço delimitado pelas duas funções, considerando que as duas sofrem rotação, mantendo o eixo como base de rotação, conforme fizemos no caso do tópico anterior com uma função, a única diferença é que temos um volume que deverá ser subtraido do outro.
Segundo o mesmo raciocínio da análise anterior, verificamos que o volume de um disco de seção do sólido no intervalo pode ser determinada como seque:
Inevitavelmente vemos a correspondência entre os dois casos, simplesmente há uma subtração de volumes, que veremos refletida no resultado final... Prosseguindo, façamos a somatória dos valores das seções dentro do intervalo quando as parcelas diminuem infinitesimalmente:
Finalmente encontramos o volume:
ou
Exemplo 3
[editar | editar código-fonte]Calcular o volume do sólido gerado pela rotação das curvas e em relação ao eixo das abscissas, considerando o intervalo entre e o ponto de encontro das duas curvas.
Antes de tudo vamos encontrar o ponto de encontro das curvas, ou seja:
As curvas se encontram quando:
Devemos encontrar o volume entre as duas curvas no intervalo :
Que nos fornece um volume aproximado de:
unidades cúbicas.
Cilindros concêntricos
[editar | editar código-fonte]Agora imaginemos um sólido cujo eixo se encontra nas ordenadas, ou seja, para cada ponto da função teremos uma circunferência, se traçarmos uma reta até o eixo das abscissas para cada ponto teremos cilindros concêntricos ao eixo das ordenadas.
Para definir o volume do cilindro consideremos:
- O intervalo para a espessura do cilindro em ;
- Chamamos de a partição:;
- Dentro de há sempre uma subpartição que é a maior, a qual chamamos de norma, identifincando-a como:
- Existindo os números de forma que ;
O volume de um pequeno segmento do cilindro é:
Somamos todos os segmentos para encontrar o volume total:
Se levarmos os subintervalos entre os valores de a números cada vez menores teremos:
ou seja:
Como podemos fazer:
Concluimos que:
ou
Exemplo 4
[editar | editar código-fonte]Encontrar o volume do sólido gerado pela rotação da curva , cujo eixo de revolução é o eixo das ordenadas, no intervalo das abscissas:
Da fórmula do cálculo temos:
Podemos usar a integração por partes e chegar a:
Temos um volume aproximado de:
unidades cúbicas.
Lâminas paralelas
[editar | editar código-fonte]Os métodos anteriormente utilizados para o cálculo de volumes podem ser englobados em um conceito geral, no qual podemos fazer a soma de pequenos segmentos de um sólido encontrando o volume total, uma forma de fazer isso é utilizar o secionamento de forma a relacionar a área de cada seção à variável independente, ou seja, se temos seções trasversais perpendiculares ao eixo da variável independente e podemos relacionar a área de cada "lâmina" ao valor da variável, temos um meio de integrar todas as lâminas e encontrar o volume do sólido com uma somatória das mesmas.
Considerando:
área da seção.
O volume é:
Uma vez que quando temos e que temos seções dentro do intervalo , onde a maior é a norma, podemos concluir que a somatória é levada, no limite, a ser a integral:
Ou seja, para que possamos encontra a área nestes casos basta encontrar a integral definida da função área; sempre que for possível encontrar uma função contínua da área da seção em relação a variável independente, poderemos encontrar o volume do sólido integrando esta função área.
Exemplo 5
[editar | editar código-fonte]Calcular o volume do sólido formado por um cilindro circular reto, cuja base tem centro na orígem dos eixos cartesianos e é paralela ao plano dentro de um raio de 4 unidades, sendo secionado por um plano que passa pelos pontos e equidistante do eixo :
Retiramos as informações do problema proposto, que nos diz que:
- A altura do cilindro para cada valor de é igual a da reta determinada
pelos pontos que pertencem ao plano, uma vez que o plano é perpendicular ao plano :
logo:
que define a reta:
- Seções do cilindro perpendiculares ao eixo tem bases que crescem a medida
que o valor de aumenta, cujo valor pode ser obtido por:
Diante disto podemos verificar que o sólido pode ser definido por seções trangulares, perpendiculares ao eixo , portanto fazemos:
Pois há faixas onde o que nos obriga a aplicar a correção. Agora vamos calcular a integral indefinida:
Se tivermos:
Substituimos:
Redefinindo:
Ou seja:
logo:
O volume é:
unidades cúbicas.
Pressão dos líquidos
[editar | editar código-fonte]Esta é uma aplicação bastante interessante... Considere que tenhamos que calcular a pressão que um líquido exerce sobre um objeto imerso em algum líquido, se o objeto é plano o cálculo dessa pressão e conseqüentemente a força total sobre a superfície é fácil de ser calculada, porém se o objeto é curvo e a força se distribui ao longo do corpo temos um problema complexo nas mãos. Investigaremos agora uma aplicação da integral para solução deste problema.
Adotemos as sequintes nomenclaturas para as definições que se seguem:
- - Pressão volumétrica;
- - Pressão superficial;
- - Força;
- - Área;
- - Volume;
- - Altura;
Então, da definição de Física, a pressão em um líquido contido num recipiente de volume é:
Ou seja, se o volume do corpo for unitário, a força que atua sobre ele é igual a presão volumétrica, porém se quisermos saber a pressão exercida pelo líquido sobre uma superfície fazemos:
ou
Porém, imaginemos que o corpo é uma lâmina mergulhada verticalmente e desejamos obter a força total exercída pelo líquido sobre o mesmo... Inevitavelmente veremos que a força aumenta com a altura e sua somatória não será algo convencional se a área da superfície do objeto for curva.
Consideremos que a largura do objeto ao longo da linha vertical que define a altura seja e a altura seja , se tomarmos uma partição onde tivervos diversos dentro de um intervalo . Ainda temos que, pelo princípio de Pascal, a pressão é a mesma em todas as direções em algum ponto do líquido, o que nos leva a concluir que:
logo:
É uma boa aproximação do valor da força, porém se fizermos com que n seja cada vez maior até valores que tendam a infinito, podemos fazer:
ou
O que nos leva a:
Exemplo 6
[editar | editar código-fonte]Comprimentos de curvas
[editar | editar código-fonte]Esta é mais uma interessante aplicação das integrais, com elas podemos calcular o comprimento de curvas utilizando uma generalização da regra do cálculo da distância entre dois pontos, a qual já conhecemos da matemática de nível médio.
Sabemos que a distância entre dois pontos é:
Se existe uma curva entre os pontos e podemos subdividir o intervalo entre os dois pontos de forma que tenhamos:
e
Propomos um índice para que tenhamos:
e
Para cada subintervalo dentro de
e
Se defirmos o ponto médio para cada subintervalo, como sendo:
A distância entre dois pontos dentro desse subintervalo é:
Uma boa aproximação do comprimento da curva pode ser encontrada fazendo-se:
Definindo uma norma para a partição no intervalo, teremos:
logo:
Exemplo 7
[editar | editar código-fonte]- Stewart, James. Cálculo. 5ª.ed. São Paulo: Pioneira, 2005. v. 1. ISBN 8522104794
- Leithold, Louis. Cálculo com Geometria Analítica. 5ª.ed. Harbra, 1994. v. 1. ISBN 8529400941
- Guidorizzi, Hamilton Luiz. Um curso de cálculo. LTC, 2005. v. 1. ISBN 8521612591
- Foulis, David J., Munem, Mustafa A.. Cálculo. 1ª.ed. LTC, 1982. v. 1. ISBN 8521610548
- Krantz, Steven George. Calculus Demystified. McGraw-Hill Professional, 2002. 343 p. ISBN 0071393080





![{\displaystyle [a,b];\ (a,b);\ ]a,b[;\ [a,b);\ (a,b];\ [a,b[;\ ]a,b]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c0f85314618f4dc84f28c72877544c71048422e)

























![{\displaystyle ]-2,4[;[-12,8[\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/529d38df27d95b95c90ae1f25db1e388682040a7)

























































































































































![{\displaystyle \lim _{x\to a}{\sqrt[{n}]{(f(x))}}\ =\ {\sqrt[{n}]{\lim _{x\to a}f(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eedb0bc0bead2ad25fcbd970822d9514461aef3a)































































![{\displaystyle f(x)=2+{\sqrt[{3}]{x-3}}+{\frac {x-3}{10}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82848de36fc5431c47d331372986f70469eafbb7)




























![{\displaystyle \lim _{x\to 0}\left[f(x+\Delta x)-f(x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fa3cc7bfa10dc52f79115ff00fb82cc84c997614)











![{\displaystyle F'(x)=\lim _{\Delta x\to 0}{\frac {\left[f(x+\Delta x)-f(x)\right]\cdot g(x+\Delta x)+f(x)\cdot \left[g(x+\Delta x)-g(x)\right]}{\Delta x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df249d0797a464dd3abed61b6bf000f8388e0ca0)
![{\displaystyle F'(x)=\lim _{\Delta x\to 0}{\frac {\left[g(x)+\Delta x\right]\cdot \left[f(x+\Delta x)-f(x)\right]}{\Delta x}}+\lim _{\Delta x\to 0}{\frac {f(x)\cdot \left[g(x+\Delta x)-g(x)\right]}{\Delta x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/99d444fc49fb303d962f73f8122f518f64c36de5)



![{\displaystyle F'(x)={\frac {g(x)\cdot f'(x)\ -\ f(x)\cdot g'(x)}{[g(x)]^{2}}}\,\!.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/679a7e0f8f8290d99f6b76e6e686d7b070c7962c)




![{\displaystyle F'(x)=\lim _{\Delta x\to 0}{\frac {g(x)\cdot \left[f(x+\Delta x)-f(x)\right]-f(x)\cdot \left[g(x+\Delta x)-g(x)\right]}{g(x)\cdot g(x+\Delta x)\cdot \Delta x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f947fa0373991ad71b04d4d5e3daf3b54d211d8)
![{\displaystyle F'(x)=\lim _{\Delta x\to 0}{\frac {g(x)\cdot \left[{\frac {f(x+\Delta x)-f(x)}{\Delta x}}\right]-f(x)\cdot \left[{\frac {g(x+\Delta x)-g(x)}{\Delta x}}\right]}{g(x)\cdot g(x+\Delta x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc8039a60d290d517c914d1cfcba48d9ff0427e8)
![{\displaystyle F'(x)={\frac {g(x)\cdot f'(x)\ -\ f(x)\cdot g'(x)}{[g(x)]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3dfc130d9895af7eb3b5529b0e778d3be820fc6)







![{\displaystyle h(x)=f[g(x)]\,\!,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b743c56c502e1f9363ec8bb0e2e4fe1049b0dd59)
![{\displaystyle h'(x)=g'(x)\cdot f'[g(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f216985ad69f91e701545cf0d5eff16cb6252496)





















![{\displaystyle f'(x)=\lim _{\Delta x\to 0}{\frac {c\cdot [g(x_{2})-g(x_{1})]}{\Delta x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27e9838e1f7e9fa0a6e3aeff56ad684a9776fa50)






![{\displaystyle f'(x)=\lim _{\Delta x\to 0}\left[n\cdot x^{n-1}+{\frac {n\cdot (n-1)\cdot x^{n-2}\cdot (\Delta x)}{2!}}+...+n\cdot x\cdot (\Delta x)^{n-2}+(\Delta x)^{n-1}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51d60826a54d3b69e4e0e1622ac9a8d3ab0f6f5e)




![{\displaystyle \left[y=\left(2-x\right){\sqrt {x+1}}+1\quad ,\quad y=\left(x-2\right){\sqrt {x+1}}+1\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ff1634b5a0ebf2b8d55b3ce4a9c8f3517402a5c)
![{\displaystyle \left[{\frac {{\mbox{d}}y}{{\mbox{d}}x}}={\frac {3x^{2}-6x}{2\left(2-x\right){\sqrt {x+1}}}}\quad ,\quad {\frac {{\mbox{d}}y}{{\mbox{d}}x}}={\frac {3x^{2}-6x}{2\left(x-2\right){\sqrt {x+1}}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/09c6a433ed44d003c1fd7e6aa92217b4e9351d6c)
![{\displaystyle \left[{\frac {{\mbox{d}}y}{{\mbox{d}}x}}={\frac {3x{\sqrt {x+1}}}{2(x+1)}}\quad ,\quad {\frac {{\mbox{d}}y}{{\mbox{d}}x}}=-{\frac {3x{\sqrt {x+1}}}{2(x+1)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d208df288b71ccea584d06565e534af2355df6f)















![{\displaystyle [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)







![{\displaystyle {c}\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8f1d041defdd2e3a9e3c9bfcf7e2e784e14801e8)


















![{\displaystyle \{[a,f(a)];[b,f(b)]\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28b7f0446a2f95fd17f557d32a27c8ef0814361f)











![{\displaystyle [x;f(x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/084ff8ae4a8719e8da2968f41f095ad09f987891)





![{\displaystyle {[(x_{2}-x_{1})>0]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a2e357a296a8cff9abc8ab39ba5524a7a012c4f0)















































































![{\displaystyle \sum _{i=1}^{n}cf(i)=c[f(1)+f(2)+f(3)+f(4)+f(5)+f(6)+\dots +f(n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfe81cd8f780733ec1eb4a34c141554da2b8ae40)
![{\displaystyle \sum _{i=1}^{n}[f(i)+g(i)]=\sum _{i=1}^{n}f(i)+\sum _{i=1}^{n}g(i)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/431a6734eddee9bc2540f34a775ebb6e17ff4305)
![{\displaystyle \sum _{i=1}^{n}[f(i)+g(i)]=[f(1)+g(1)]+[f(2)+g(2)]+[f(3)+g(3)]+\dots +[f(n)+g(n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d48727c99c25f928c63559f615531d4bfd1ea4d3)
![{\displaystyle \sum _{i=1}^{n}[f(i)+g(i)]=[f(1)+f(2)+f(3)+\dots +f(n)]+[g(1)+g(2)+g(3)+\dots +g(n)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9fa44875c53e61573869287d3cb16b931d283f79)
![{\displaystyle \sum _{i=1}^{n}[f(i)-f(i-1)]=f(n)\ -\ f(0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad417b61317518758879a08be6910c87c4449d5f)
![{\displaystyle \sum _{i=1}^{n}[f(i)-f(i-1)]=f(1)\ -\ f(0)+f(2)\ -\ f(1)+f(3)\ -\ f(2)+f(4)\ -\ f(3)-\dots +f(n)-f(n-1)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee6f0a3dcc5dbcb9d5da8ff6c88100a1fa2ed174)
![{\displaystyle \sum _{i=1}^{n}[f(i)-f(i-1)]=-f(0)+f(n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0521f9c76c784a62808f7d3ee1d05f47dfb62d9e)





![{\displaystyle [{\xi }_{n}\ ,\ f({\xi }_{n})]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c82d62dd4c16c5bbfdd0740503360392292fca0c)



















![{\displaystyle \int _{a}^{b}[f(x)+g(x)]{\mbox{d}}x=\int _{a}^{b}f(x){\mbox{d}}x+\int _{a}^{b}g(x){\mbox{d}}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08baec48584dab827cd35f9d82e2da80388ad248)
![{\displaystyle \int _{a}^{b}[f(x)+g(x)]{\mbox{d}}x=\lim _{\left\|\Delta \right\|\to 0}\sum _{i=1}^{n}[f({\xi }_{i})\ +\ g({\xi }_{i})]{\Delta }_{i}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6bbdf6e0258d119dcb49ad22f8fd8d24f24ff079)
![{\displaystyle \int _{a}^{b}[f(x)+g(x)]{\mbox{d}}x=\lim _{\left\|\Delta \right\|\to 0}\sum _{i=1}^{n}f({\xi }_{i}){\Delta }_{i}x\ +\ \lim _{\left\|\Delta \right\|\to 0}\sum _{i=1}^{n}g({\xi }_{i}){\Delta }_{i}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b89f6be7313bea17c44b11c72ba643541ffb53c)












![{\displaystyle M={\frac {1}{b-a}}\cdot \left[\lim _{\left\|\Delta \right\|\to 0}\sum _{i=1}^{n}f({\xi }_{i})\Delta x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fcffedcc390d3d6efff99df94a8e0cac8781e75d)

















































































































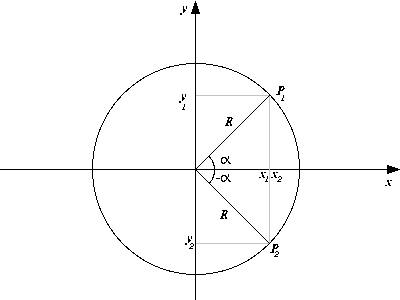















































![{\displaystyle [\cos(a+b)-1]^{2}+sen^{2}(a+b)=[\cos(b)-\cos(-a)]^{2}+[\ {\mbox{sen}}(b)-\ {\mbox{sen}}(-a)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d04fcd4d09bab1f4c2c112b95fb157a88b5b37b2)


![{\displaystyle -2\cos(a+b)+1+1=[cos^{2}(b)+sen^{2}(b)]-2\cos(-a)\cos(b)+[cos^{2}(-a)+sen^{2}(-a)]-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b840144aa4a86b8c5d3424fee8d1d141bd2f31e)












![{\displaystyle \cos \left[{\frac {\pi }{2}}-(a+b)\right]=\ {\mbox{sen}}(a+b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd9f634ed48aa13591bf734a34c5b1ce59ef9069)
![{\displaystyle \ {\mbox{sen}}(a+b)=\cos \left[{\frac {\pi }{2}}-(a+b)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8c5ab130bf7dded58488fc9cb3bbcd43efe11)
![{\displaystyle \ {\mbox{sen}}(a+b)=\cos \left[\left({\frac {\pi }{2}}-a\right)-b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abdf829b687311359cc480dc53fbc660b49b1ee1)





![{\displaystyle \ {\mbox{sen}}(a)\ {\mbox{sen}}(b)={\frac {1}{2}}\cdot [\cos(a-b)-\cos(a+b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb203fea1e1f845d38253c9c60193a53f9b8e36e)

![{\displaystyle \cos(a)\cos(b)={\frac {1}{2}}\cdot [\cos(a+b)+\cos(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01b00d9444f433bda7933bad95f1af6e8bb43f0e)

![{\displaystyle \ {\mbox{sen}}(a)\cos(b)={\frac {1}{2}}\cdot [\ {\mbox{sen}}(a+b)+\ {\mbox{sen}}(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc9c683868805fb4106f5b846ac35431f66f408b)















![{\displaystyle n^{2}=sen^{2}(\alpha )+[1-\cos(\alpha )]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3373441ef3dff5f42c31fa5b25e19b8f31153a25)
![{\displaystyle n^{2}=2[1-\cos(\alpha )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d864fba4442558a36fb56b3d458c3f59c07c04f1)


![{\displaystyle \ {\mbox{sen}}(\alpha )=n\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d61538f94bda9ad43f26de5f4b0aa74c0507fc)
![{\displaystyle \left[\lim _{\alpha \to 0}{\frac {1}{\alpha }}=\lim _{n\to 0}{\frac {1}{n}}\right]\cdot \ {\mbox{sen}}(\alpha )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f496d310739c0d9038f0e35f221ff025ae85ab5)

![{\displaystyle \lim _{\alpha \to 0}{\frac {\ {\mbox{sen}}(\alpha )}{\alpha }}=\lim _{n\to 0}\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c9815b44a77aa6c2d4d8f5b9af77100302398e5)















![{\displaystyle [\cos(\alpha ),\ {\mbox{sen}}(\alpha )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d470bb7a97f7e5f282d6ba68de12784e2fa5fde0)


























![{\displaystyle f\ '(x)={\frac {\cos(x)\cos(x)-\ {\mbox{sen}}(x)[-\ {\mbox{sen}}(x)]}{\cos ^{2}(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1e957d888c735ab71f69d1522adc33ce71156295)






















![{\displaystyle du=[\sec(x)\ {\mbox{tg}}(x)+\sec ^{2}(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4cd134951974266ec76a2505f85640327550129a)
















![{\displaystyle f\ '(x)={\frac {\ {\mbox{sen}}(x)[-\ {\mbox{sen}}(x)]-\cos(x)\cos(x)}{\ {\mbox{sen}}^{2}(x)}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/36e7ab0d4a5a78056f1e90d17f9c8be4f14dfef8)
















![{\displaystyle du=[-\ {\mbox{cosec}}^{2}(x)+\ {\mbox{cotg}}(x)\ {\mbox{cosec}}(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5917b9698e6b497ef310cee4452043b5c0f0d0fc)




![{\displaystyle \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54381f086ac9ffe8306d413f813abcb616e95dee)
![{\displaystyle \left[0,\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8e34615383b8ffe6f079cfd094c2b274fab51a4)
![{\displaystyle y=\ {\mbox{arcsen}}(x)\ \exists \quad \forall \ x=\ {\mbox{sen}}(y)\land y\in \ \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/751268dc9cfdf45fcaafd9f8c812264a5363d2a0)
![{\displaystyle y=\ {\mbox{arccos}}(x)\ \exists \quad \forall \ x=\cos(y)\land y\in \ \left[0,\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0bfb7219c6b1e33f86f4382cb59d6fcc9b2e9ab7)







































![{\displaystyle {\frac {dz}{dx}}=0-{\frac {d[arctg(z)]}{dx}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aa86f84ede174b7c7dbf65932eabef4a7219dfd)







![{\displaystyle (-\infty ,-1]\quad ;\quad [1,\infty )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/67f8f1d101f6e08597b0c080fd3682ae6804655f)








![{\displaystyle {\frac {d[\ {\mbox{arccos}}(t)]}{dx}}=-{\frac {1}{\sqrt {1-t^{2}}}}\left({\frac {dt}{dx}}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/15f21199beb34b4f2aa0fb569da320de53e59ea8)


















































































































































![{\displaystyle {\frac {dy}{dx}}={\frac {d[\ {\mbox{argtgh}}(x)]}{dx}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e49016992d4c0575ecaa43557ce73dc6393b9ac1)
![{\displaystyle {\frac {dy}{dx}}={\frac {1}{2}}\left({\frac {1-x}{1+x}}\right)\left[{\frac {1-x-(1+x)(-1)}{(1-x)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/afef3db735e964ead4ef283068f1954c0b180d65)
![{\displaystyle {\frac {dy}{dx}}={\frac {1}{2}}\left({\frac {1-x}{1+x}}\right)\left[{\frac {2}{(1-x)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6022458c1510b006f68794b47eea4b6bd0d1a77)
![{\displaystyle {\frac {dy}{dx}}={\frac {1}{2}}\left[{\frac {2}{(1+x)(1-x)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ff0b6d491a3f3ba8f125c0eb46c562a35585a47)



![{\displaystyle {\frac {dy}{dx}}={\frac {d[{\mbox{argsenh}}(x)]}{dx}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bda5db26d6b8bb31008ac7932698af138058b439)
![{\displaystyle {\frac {dy}{dx}}={\frac {x}{1-{\sqrt {1-x^{2}}}}}\left[{\frac {x{\frac {-(-2x)}{2{\sqrt {1-x^{2}}}}}-\left(1-{\sqrt {1-x^{2}}}\right)}{x^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e22be4ba8703e027fa95fc5b396fdc1b6e949b3)
























![{\displaystyle {\frac {dy}{dx}}={\frac {d[\ {\mbox{argcotgh}}(x)]}{dx}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/23aded978478393f1c847a6cccfb15e1b563ac21)
![{\displaystyle {\frac {dy}{dx}}={\frac {1}{2}}\left({\frac {x+1}{x-1}}\right)\left[{\frac {x+1-(x-1)}{(x+1)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/180f3299ef85e235defa1014a1365bdbb74626a4)
![{\displaystyle {\frac {dy}{dx}}={\frac {1}{2}}\left({\frac {x+1}{x-1}}\right)\left[{\frac {2}{(x+1)^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c4b3e8504fbfbff2e61d83ae1f48510dcdfcaa4)
![{\displaystyle {\frac {dy}{dx}}={\frac {1}{2}}\left[{\frac {2}{(x-1)(x+1)}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d0b52fd905f5c9fb64d1784c74f538c9294d190)


![{\displaystyle {\frac {dy}{dx}}={\frac {d[{\mbox{argcosh}}(x)]}{dx}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6088a737f776c3bcb23c8f696d214f8d4f47a60d)
![{\displaystyle {\frac {dy}{dx}}={\frac {x}{1-{\sqrt {1+x^{2}}}}}\left[{\frac {x{\frac {-2x}{2{\sqrt {1+x^{2}}}}}-\left(1-{\sqrt {1+x^{2}}}\right)}{x^{2}}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f89756a910861a036dbf984564c11202735a9b8)






















![{\displaystyle \int \ln(x)dx=x[\ln(x)-1]+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e79ea63109813cfc288c56ff999e093c753a65)
![{\displaystyle \int \ln(x)dx=x[\ln(x)-\ln(e)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/599baa5d0ea5d5bd2e596b22e5d52615499e2f70)
![{\displaystyle \int \ln(x)dx=x\left[\ln \left({\frac {x}{e}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29f63770193e07e4860d17e3c8cbf9d3ccd65740)






















![{\displaystyle {\frac {d[arctg(x)]}{dx}}={\frac {1}{1+x^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48860b431d11c2959b8808f5de357e96f78ac25b)


















![{\displaystyle \int sec^{3}(x)dx=sec(x)tg(x)-\int tg(x)[sec(x)tg(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cf5e37988fa82a38852c526b205595163018f4f)

![{\displaystyle \int sec^{3}(x)dx=sec(x)tg(x)-\int sec(x)[sec^{2}(x)-1]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2659d444bdb673cf5587572befb4de6652e44efa)














![{\displaystyle f(\theta )={\sqrt {a^{2}-\left[a\ sen(\theta )\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5db6d9db06eb2aa430ab1d364bc57ec42124d4)



























![{\displaystyle F(\theta )=\int {\frac {2\cdot cos(\theta )d{\theta }}{\sqrt {4-\left[2\cdot sen(\theta )\right]^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e16638aa9368d7e592c75fea436247ab4668102)











































![{\displaystyle A[(-2)-1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c96fcc52fa1c61e5ed861991565e03d8b8d11f0f)


![{\displaystyle B[(1)+2]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bafe62e70cda2d0f4ec660e481719262286ca321)








































}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb9b03c6e9d48e4a47d7d2676108f1190c34244e)







![{\displaystyle F(x)={\frac {x^{2}}{2}}+x+\ln \left[|x-1|\cdot \left(x^{2}+1\right)^{\frac {1}{2}}\right]+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f8866005d412dee378f5efe565cb1b42638392e)
























































![{\displaystyle dt={\frac {1}{2}}\left[1+tg^{2}\left({\frac {x}{2}}\right)\right]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b6a96d218c15a649bfad0098634f9bcf135091)














![{\displaystyle {[a,h(a)]}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b10e11947df507d5b42c74fd43563ba02a9d4bb)




![{\displaystyle [a,h(a)]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3e64c42ea4bc1b3ef7258ab6844cc5442a1724a7)








![{\displaystyle [a,b]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/08268f073d76e500a09a309a45bcc9f19e599db4)





![{\displaystyle [c,h(c)]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f60f88a7807ef8d7711612e9c3c5d8fe978aa3a8)






















![{\displaystyle [\ a;\ b]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/116f290ab65f53feaddcadde8460fed4533d13f3)































![{\displaystyle [a,x]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4054d5a553f467f7714e54cf337ce9e5d157df43)







![{\displaystyle z=\left[f\ '(a)(x-a)-f\ '(x)(x-x)\right]+\int _{a}^{x}(x-u)f\ ''(u)du\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b0409703d07b61d95afd8c2df6343b6a6e70ea5)



![{\displaystyle z=f\ '(a)(x-a)+\left[{\frac {f\ ''(a)(x-a)^{2}}{2!}}-{\frac {f\ ''(x)(x-x)^{2}}{2!}}\right]+\int _{a}^{x}{\frac {(x-u)^{2}}{2!}}f^{(3)}(u)du\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/25436c8529229d3efe3fb8a22a9d5282d7448283)

























![{\displaystyle A_{1}=\left[{\frac {x^{3}}{3}}\right]_{0}^{3}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c53a1c408eb50e8dd9c41e4db5e34a47068085b)
![{\displaystyle A_{1}=\left[{\frac {(3)^{3}}{3}}-{\frac {(0)^{3}}{3}}\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f36fe80c2276091f9645baf4579f094273731d5)



![{\displaystyle A_{2}=\left[{\frac {3x^{2}}{2}}\right]_{0}^{3}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45873868a7b383539614276ae0d6813d18bc11f9)
![{\displaystyle A_{2}=\left[{\frac {3(3)^{2}}{2}}-{\frac {3(0)^{2}}{2}}\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1fd7782da50aae03036c448b7f4e814f58b9342)






![{\displaystyle V_{d}(\xi _{i})=\pi [f(\xi _{i})]^{2}\Delta _{i}x\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5ec6e3d760cf6b1ad6f18a150fba043dc9728990)

![{\displaystyle V=\int _{a}^{b}\pi [f(x)]^{2}dx\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e4208b321c16ab93d76693390f0271949ce3c05b)
![{\displaystyle V=\pi \int _{a}^{b}[f(x)]^{2}dx\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f325809dcc2394d371798e8fcc8a85a068c834e5)

![{\displaystyle [0,3]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54bea80f996e54574a517adbe3ff6ed393a91b0f)








![{\displaystyle V_{d}(\xi _{i})=\pi \{[f(\xi _{i})]^{2}-[g(\xi _{i})]^{2}\}\Delta _{i}x\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6f1a3b1469f13fcd62b05251554e702ed40051d8)
![{\displaystyle V=\int _{a}^{b}\pi \{[f(x)]^{2}-[g(x)]^{2}\}dx\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a22d99f015b53e8076080703f12b846ebb7ef5e2)
![{\displaystyle V=\pi \int _{a}^{b}\{[f(x)]^{2}-[g(x)]^{2}\}dx\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a197ce32a14db1b85103cc64e57df041373b2490)





![{\displaystyle [0,4]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6ac637da059a8a345d6b998d803833127d544714)
![{\displaystyle V=\pi \int _{0}^{4}\left[\left(32{\sqrt {x}}\right)^{2}-\left(x^{3}\right)^{2}\right]dx\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48405c1b26f8b32e8b395d17e4e4df1c287cd6e6)


![{\displaystyle V=\pi \left[512\cdot (4)^{2}-{\frac {(4)^{7}}{7}}\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1d4239d5db2e7cd267e31e1f436bb4a4ba5c862)














![{\displaystyle [3,6]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/58d3d1fddac37a617324052fcc8804e644ef7668)

![{\displaystyle V=2\pi \left[{\frac {2x}{3}}(x-3)^{\frac {3}{2}}\right]_{3}^{6}-{\frac {2}{3}}\int _{3}^{6}(x-3)^{\frac {3}{2}}dx\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35c37fdd7f87d21a41575058a7044924a0a35131)
![{\displaystyle V=2\pi \left[{\frac {2x}{3}}(x-3)^{\frac {3}{2}}-{\frac {4}{15}}(x-3)^{\frac {5}{2}}\right]_{3}^{6}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0754e2e98453fda93b2ddfd3dbeac71c7d1bcc0f)
![{\displaystyle V=2\pi \left[{\frac {2(6)}{3}}(6-3)^{\frac {3}{2}}-{\frac {4}{15}}(6-3)^{\frac {5}{2}}\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1677bd9b7261a4bd94be985f0a20797e0b500cf5)




















































![{\displaystyle \left[\xi _{i},f(\xi _{i})\right]\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1837c62570161bb2b3e41d21d5d6289ef928ed8b)




