A integração é um processo que demanda certa habilidade e técnica, ele provê um meio indispensável para análises de cálculos diversos, além disso o meio de integrar certas funções deve ser exercitado até que sejamos capazes de absorver a sua essência. O problema da integração deve ser visto como uma análise que pode conduzir a resultados algébricos diversos, quando tomadas técnicas diversas, que concordam, porém, em resultado numérico.
Devido à necessidade de exercício dessas técnicas que apresentaremos, teremos mais exemplos neste capítulo, uma ótima maneira de introduzir o conteúdo enquanto a teoria é exposta. A natureza diversa das formas de integrais nos obriga a fazer este estudo a parte, pois certas funções são peculiarmente difíceis de serem analisadas antes da utilização de algum artifício que permita sua simplificação, este é o objetivo deste capítulo: trazer ao leitor os processos de integração e as diversas possibilidades de simplificação de funções para a aplicação destes processos.
A técnica de integração por partes consiste da utilização do conceito de diferencial inversa aplicado à fórmula da regra da diferencial do produto, ou seja:

Que após a antidiferencial se torna:


E, portanto:

A utilização desta fórmula para melhorar o processo de integração implica na necessidade de uma breve explanação, o processo consiste em observar a função a ser integrada como sendo uma integral  , ou seja, devemos separar a função em duas partes: uma, chamamos de u, que consideraremos função primitiva e outra dv que será uma diferencial, desta forma, faremos a integração da parte dv para encontrar v e depois subtrairemos a integral da mesma com relação a diferncial de u: du. Parece um tanto incomun a princípio, porém após o hábito no uso da técnica, esta se torna muito útil.
, ou seja, devemos separar a função em duas partes: uma, chamamos de u, que consideraremos função primitiva e outra dv que será uma diferencial, desta forma, faremos a integração da parte dv para encontrar v e depois subtrairemos a integral da mesma com relação a diferncial de u: du. Parece um tanto incomun a princípio, porém após o hábito no uso da técnica, esta se torna muito útil.
Outro fato deve ser explorado: como o processo demanda a integração da diferencial dv nos vem a questão sobre a necessidade de utilização da constante de antidiferenciação C, portanto façamos a verificação da fórmula utilizando-a:
Se  ,
,





Ou seja, a constante é dispensável para o cálculo da integral que resulta em v.
Utilização da integração por partes na resolução da integral do logaritmo natural:

Separamos a diferencial dx e a primitiva  , procedendo as operações inversas:
, procedendo as operações inversas:

depois:


Aplicando à fórmula de integração por partes:



![{\displaystyle \int \ln(x)dx=x[\ln(x)-1]+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e79ea63109813cfc288c56ff999e093c753a65)
Também há os que preferem simplificar mais, desta forma:
![{\displaystyle \int \ln(x)dx=x[\ln(x)-\ln(e)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/599baa5d0ea5d5bd2e596b22e5d52615499e2f70)
![{\displaystyle \int \ln(x)dx=x\left[\ln \left({\frac {x}{e}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29f63770193e07e4860d17e3c8cbf9d3ccd65740)

Sendo C a constante de antidiferenciação.
Utilização da integração por partes para encontrar a integral do arcseno:

Separamos as partes e operamos para encontrar as respectivas inversas:

Assim:


Aplicando à fórmula da integração por partes:

agora consideremos o seguinte:



logo:



Portanto:

Sendo C a nossa tradicional constante de antidiferenciação.
Utilização da integração por partes para encontrar a integral do arccosseno:

Separamos as partes e operamos para encontrar as respectivas inversas:

depois:


Aplicando à fórmula da integração por partes:

agora consideremos o seguinte:



logo:



Portanto:

Sendo C a nossa tradicional constante de antidiferenciação.
Utilizando a integração por partes para encontrar a integral do arctangente:

Separando as partes e operando as inversas:

e
![{\displaystyle {\frac {d[arctg(x)]}{dx}}={\frac {1}{1+x^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48860b431d11c2959b8808f5de357e96f78ac25b)
Aplicamos a fórmula da integração por partes:

Por outro lado:


onde podemos extrair:

voltando ao desenvolvimento da integral:



Portanto:

Novamente, temos C como contante de antidiferenciação.
Este é um exemplo que nos revela uma função claramente divisível em duas partes:

Considerando as partes:


e:

Substituindo na fórmula de integração por partes:

O segundo lado desta expressão pode ser novamente simplificado, aplicando a integração por partes mais uma vez:


Portanto:

Utilizando a integração por partes para resolução da integral de secantes com expoente maior que 2:

Podemos fazer:

E aplicar a integração por partes:
![{\displaystyle \int sec^{3}(x)dx=sec(x)tg(x)-\int tg(x)[sec(x)tg(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cf5e37988fa82a38852c526b205595163018f4f)

![{\displaystyle \int sec^{3}(x)dx=sec(x)tg(x)-\int sec(x)[sec^{2}(x)-1]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2659d444bdb673cf5587572befb4de6652e44efa)



E finalmente:

Com C constante.
A existência de relações algébricas que nos levam a arcos nos traz a possibilidade de converter uma expressão algébrica, conseqüentemente uma função algébrica, em uma função trigonométrica. A possibilidade de lidar com certas funções de forma trigonométrica nos leva à utilizar os artifícios das identidades para a simplificação dessas.
Três funções algébricas têm semelhanças com funções trigonométricas que são notoriamente úteis para a simplificação de algumas funções, elas são:



Sendo "a" constante.
Note que as expressões são meramente relações quadráticas que descendem da relação quadrática entre todos os lados de um mesmo triângulo:  , se escolhermos um par (variável,constante) e substituirmos na equação teremos as expressões acima como resultantes, teremos uma variável dependente para cada par (variável,constante), por exemplo: se fizermos
, se escolhermos um par (variável,constante) e substituirmos na equação teremos as expressões acima como resultantes, teremos uma variável dependente para cada par (variável,constante), por exemplo: se fizermos  ,
,  e
e  teremos a expressão (2) como resultante (y).
teremos a expressão (2) como resultante (y).
Imagine que temos uma nova variável  e que:
e que:

Sendo: 
Podemos dizer que:
![{\displaystyle f(\theta )={\sqrt {a^{2}-\left[a\ sen(\theta )\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5db6d9db06eb2aa430ab1d364bc57ec42124d4)



Portanto:
 quando
quando  e
e 
O exposto acima encontra respaudo no fato de que a expressão é simplesmente a tradução da relação métrica de um triângulo retângulo para definição do cosseno a partir do seno, como segue:
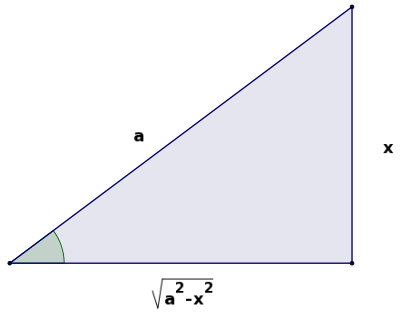
Se fizermos a comparação entre as funções e o gráfico acima, substituindo as variáveis e constantes de acordo com a função dada, teremos o seguinte:
- Na função
 é uma tangente;
é uma tangente;
- Na função
 é um seno;
é um seno;
- Na função
 é uma secante.
é uma secante.
O que nos dá as substituições:
| Expressão
|
Substituição
|

|

|

|

|

|

|
Agora, considere o fato de que a função  tem como integral a função
tem como integral a função  , então podemos fazer:
, então podemos fazer:

Uma vez, que pela análise anterior já sabemos que quando fazemos  temos:
temos:

então:

Temos que encontrar  :
:


O que nos revela algo interessante:


Ou seja:

Logo:

Seja a função:  , calculemos a sua integral por substituição trigonométrica:
, calculemos a sua integral por substituição trigonométrica:

Fazendo a transformação de variáveis:


A integral será:
![{\displaystyle F(\theta )=\int {\frac {2\cdot cos(\theta )d{\theta }}{\sqrt {4-\left[2\cdot sen(\theta )\right]^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e16638aa9368d7e592c75fea436247ab4668102)




Como:


Portanto:

Sendo C a constante de antidiferenciação.
Seja a função:  , calculemos a sua integral por substituição trigonométrica:
, calculemos a sua integral por substituição trigonométrica:
Se

Introduzimos a variável angular  , de forma que:
, de forma que:

e sua diferencial:

Substituindo na equação anterior:





Retornando a função ao domínio da variável x:


Portanto:

Sendo C a constante de antidiferenciação.
Seja a função:  , calculemos a sua integral por substituição trigonométrica:
, calculemos a sua integral por substituição trigonométrica:
Se

Introduzimos a variável angular  , de forma que:
, de forma que:

e sua diferencial:

Substituindo na equação anterior:





Retornando a função ao domínio da variável x:


Portanto:

Sendo C a constante de antidiferenciação.
Denominadores de segundo grau ou mais são um pouco mais problemáticos quando queremos definir uma integral, por exemplo:
Seja a função: 
É possível demonstrar que a função pode ser fatorada da seguinte forma:

Onde A e B são os fatores a serem definidos; o processo para definí-los será explicado mais adiante e  são as raízes da equação formada a partir do denominador quando o igualamos a zero.
são as raízes da equação formada a partir do denominador quando o igualamos a zero.
Porém a demonstração disto está fora do escopo deste livro, deve ser tratado na algebra avançada.
Em todo caso, o teorema é bastante útil para a simplificação de tais funções.
As funções racionais do formato:  têm uma característica bem interessante, os seus denominadores
têm uma característica bem interessante, os seus denominadores  , quando fatorados em partes lineares e quadráticas permitem que possamos escrever a referida função como uma soma:
, quando fatorados em partes lineares e quadráticas permitem que possamos escrever a referida função como uma soma:


Seja a função  , podemos simplificá-la desta forma:
, podemos simplificá-la desta forma:
Considerando as raízes da equação  , podemos dizer que:
, podemos dizer que:

Os fatores  são calculados fazendo:
são calculados fazendo:


logo, as raízes permitem:  , então temos que admitir que ao analisar cada raiz:
, então temos que admitir que ao analisar cada raiz:
Quando  :
:
![{\displaystyle A[(-2)-1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c96fcc52fa1c61e5ed861991565e03d8b8d11f0f)

Quando  :
:
![{\displaystyle B[(1)+2]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bafe62e70cda2d0f4ec660e481719262286ca321)

então, podemos fazer:

O artifício de encontrar componentes lineares para substituir os denominadores, como exposto no tópico anterior, permite uma boa simplificação de integrais com denominadores polinomiais de graus superiores, porém ainda depende da determinação das raízes do polinômio dos denominadores, o que limita a nossa capacidade de resolução aos polinômios biquadráticos. Sem levar em conta este fato, podemos simplificar a integral para uma boa parcela de problemas que apresentam estes formatos de expressões.
Vejamos o caso anterior:
A função:
 ,
,
pode ser substituída por:

O que nos permite fazer:

Com C Constante.
Utilizando a decomposição de funções racionais em funções de denominadores lineares para a simplificação de integrais.
Seja a função:

Encontremos a integral:

Devemos simplificar a função, para isto podemos efetuar a divisão polinomial, que resulta:

Ainda resta uma parte fracionária que podemos decompor usando o método que já vimos neste capítulo:

As raízes nos revelam que:

logo podemos fazer:

ou

Analisando os valores da equação quando x se iguala as raízes:
Para  :
:


Para  :
:


Podemos concluir que:

Desta forma temos a função simplificada:

Podemos integrá-la:




Portanto:

Sendo C a constante de antidiferenciação.
A segunda categoria de funções racionais às quais temos que nos aplicar são as que dão origem a denominadores quadráticos.
Quando não temos como encontrar as raízes de certos denominadores quadráticos podemos mantê-los e utilizar a seguinte substituição:

O teorema que estabelece esta relação faz parte da álgebra avançada, portanto não entraremos em detalhe neste livro, porém faremos uso de suas consequências como forma de simplificação, como fizemos com a decomposição de denominadores em fatores lineares vista na seção anterior.
A melhor maneira de definir a parte  é substituir a variável x nesta fazendo-a igual a derivada do denominador, ou seja:
é substituir a variável x nesta fazendo-a igual a derivada do denominador, ou seja:


No lado esquerdo da equação acima, se houver variáveis de expoente maior que o maior expoente do lado direito devemos proceder uma simplificação efetuando a divisão dos polinômios, caso contrário teríamos:


Separamos cada fator de acordo com o grau da variável, obtendo:
Para 
Para 
logo:
 e
e 
Porém em funções racionais mais comuns temos que lidar com funções com partes lineares e quadráticas, onde o processo de encontrar os valores para  depende das outras partes envolvidas, para verificar o processo, vejamos o próximo exemplo...
depende das outras partes envolvidas, para verificar o processo, vejamos o próximo exemplo...
Utilizando a decomposição de funções racionais com denominadores quadráticos para simplificar o cálculo da integral.
Seja a função:

Calculemos a sua integral indefinida:

Antes de tudo façamos a simplificação dos polinômios, primeiro faremos a divisão simples do numerador pelo denominador:


Da divisão separamos a parte do resto:

Procedendo a decomposição dos fatores:

Que nos permite fazer:

}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb9b03c6e9d48e4a47d7d2676108f1190c34244e)

Quando separamos os fatores para cada variável de expoente correspondente em ambos os lados da equação, temos:

Resolvendo o sistema linear temos:

Podemos escrever a função como:

Agora podemos integrá-la:

Numa conclusão imediata podemos dizer que:

Porém em estudos onde se exige um tratamento mais algébrico com exponenciais e logaritmos, podemos adotar um formato como este:

Portanto:
![{\displaystyle F(x)={\frac {x^{2}}{2}}+x+\ln \left[|x-1|\cdot \left(x^{2}+1\right)^{\frac {1}{2}}\right]+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f8866005d412dee378f5efe565cb1b42638392e)
Com C constante.
Se podemos fazer substituições trigonométricas em funções algébricas e existem funções hiperbólicas, por que não utilizar o mesmo método de substituição com funções hiperbólicas? Temos mais esta possibilidade para simplificar a integração de funções algébricas; Detalharemos nesta seção as formas de substituição com funções hiperbólicas, que podem ser uma valorosa ferramenta para a integração de funções mais complexas.
Como conseqüência das derivadas de funções hiperbólicas inversas, temos as seguintes integrais:
| Função:
|
Derivada:
|
Integral relacionada:
|

|

|

|

|
 , , 
|

|

|
 , , 
|

|

|
 , , 
|

|

|
 , , 
|

|

|
 , , 
|

|
A técnica aqui exposta é semelhante à abordada na seção Transformando expressões algébricas em trigonométricas, a diferença básica está nas expressões a serem substituídas, uma vez que as identidades trigonométricas e hiperbólicas são sutilmente distintas, as expressões seguem a mesma tendência. Então vamos ver quais são as correspondentes algébricas para as funções hiperbólicas:
- Na função
 é um seno hiperbólico;
é um seno hiperbólico;
- Na função
 é uma tangente hiperbólica;
é uma tangente hiperbólica;
- Na função
 é uma cotangente hiperbólica.
é uma cotangente hiperbólica.
O que nos dá as substituições:
| Expressão
|
Substituição
|

|

|

|

|

|

|
Em todas as substituições consideramos um triângulo retângulo cujo vértice relacionado ao ângulo  faz parte de uma perspectiva hiperbólica, ou seja, o ângulo está em
faz parte de uma perspectiva hiperbólica, ou seja, o ângulo está em  , trata-se de uma abstração que pode ser comprovada em cálculo avançado, o nosso objetivo aqui é de fornecer as ferramentas necessárias para análises desse tipo.
, trata-se de uma abstração que pode ser comprovada em cálculo avançado, o nosso objetivo aqui é de fornecer as ferramentas necessárias para análises desse tipo.
Considere a função:  e que sua integral seja:
e que sua integral seja:  , então teremos:
, então teremos:

Concebemos uma nova variável  de forma que:
de forma que:

conseqüentemente, sua diferencial é:

Substituindo na equação inicial, temos:




Ou seja:

Porém, devido a natureza exponencial das funções hiperbólicas inversas, ainda podemos transformar esta equação na forma puramente logarítmica:

Finalmente:

O problema da integração de funções racionais trigonométrica consiste, basicamente, na característica da complexibilização progressiva quando estas funções são submetidas às técnicas convencionais de substituição, no momento que tentamos substituir a expressão original temos que definir sua diferencial, o que implica na criação de mais um termo a ser incorporado a expressão original.
Digamos que tenhamos que integrar a função:

Ao adotarmos a linha tradicional de substituições teremos:

e

no entanto:




logo teremos que integrar:

de forma que:

Que, pelo menos, é uma função algébrica pura, mas que ainda demanda um certo trabalho para ser integrada... Portanto concluimos que o processo de substituição de variáveis e diferenciais não ajuda muito.
Nesta seção exporemos um método de substituição mais eficiente para estes casos.
Apresentamos duas identidades que serão muito úteis para a simplifição de funções racionais trigonométricas, são elas:
- Seno em forma algébrica
- Cosseno em forma algébrica
Basicamente são resultantes de um processo de substituição mais bem estruturado, para possibilitar a simplificação da integração.
A identidade relacionada ao Cosseno é apresentada antes da relacionada ao seno pois será útil para a sua dedução.
Considere a seguinte definição:

logo, é dedutível que:

Considerando a identidade I-2 Cosseno da soma, temos, por conseqüência:

Se  :
:

ou

Por outro lado:




Substituindo na identidade temos:

que nos dá:

Ainda considerando a definição:

também é dedutível que:

Da identidade anterior:

Da I-1 Identidade relacional básica:

Fazendo as substituições:



logo:

Temos duas funções trigonométricas fundamentais na forma algébrica para substituir as originais na forma trigonométrica, porém para integrar as funções racionais substituindo-as por estas temos que encontrar uma diferencial correspondente para esta nova variável algébrica que criamos.
Da definição inicial:

Diferenciando:

Da identidade I-14 Relacionando tangente e secante:
![{\displaystyle dt={\frac {1}{2}}\left[1+tg^{2}\left({\frac {x}{2}}\right)\right]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b6a96d218c15a649bfad0098634f9bcf135091)

de onde concluimos que:

Agora podemos encontrar a integral proposta no início da seção:

para  , temos:
, temos:

ou seja:

Não é incrível? !!!

e

Jamais poderemos nos esquecer de C, a famigerada constante de antidiferenciação que tanto nos persegue.
Para auxiliar nos cálculos, consulte a
tabela de integrais na wikipédia



















![{\displaystyle \int \ln(x)dx=x[\ln(x)-1]+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18e79ea63109813cfc288c56ff999e093c753a65)
![{\displaystyle \int \ln(x)dx=x[\ln(x)-\ln(e)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/599baa5d0ea5d5bd2e596b22e5d52615499e2f70)
![{\displaystyle \int \ln(x)dx=x\left[\ln \left({\frac {x}{e}}\right)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/29f63770193e07e4860d17e3c8cbf9d3ccd65740)






















![{\displaystyle {\frac {d[arctg(x)]}{dx}}={\frac {1}{1+x^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48860b431d11c2959b8808f5de357e96f78ac25b)


















![{\displaystyle \int sec^{3}(x)dx=sec(x)tg(x)-\int tg(x)[sec(x)tg(x)]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5cf5e37988fa82a38852c526b205595163018f4f)

![{\displaystyle \int sec^{3}(x)dx=sec(x)tg(x)-\int sec(x)[sec^{2}(x)-1]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2659d444bdb673cf5587572befb4de6652e44efa)














![{\displaystyle f(\theta )={\sqrt {a^{2}-\left[a\ sen(\theta )\right]^{2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5db6d9db06eb2aa430ab1d364bc57ec42124d4)






























![{\displaystyle F(\theta )=\int {\frac {2\cdot cos(\theta )d{\theta }}{\sqrt {4-\left[2\cdot sen(\theta )\right]^{2}}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e16638aa9368d7e592c75fea436247ab4668102)











































![{\displaystyle A[(-2)-1]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c96fcc52fa1c61e5ed861991565e03d8b8d11f0f)


![{\displaystyle B[(1)+2]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bafe62e70cda2d0f4ec660e481719262286ca321)









































}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb9b03c6e9d48e4a47d7d2676108f1190c34244e)







![{\displaystyle F(x)={\frac {x^{2}}{2}}+x+\ln \left[|x-1|\cdot \left(x^{2}+1\right)^{\frac {1}{2}}\right]+C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f8866005d412dee378f5efe565cb1b42638392e)































































![{\displaystyle dt={\frac {1}{2}}\left[1+tg^{2}\left({\frac {x}{2}}\right)\right]dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8b6a96d218c15a649bfad0098634f9bcf135091)






