O estudo das funções deste capítulo refere-se às funções não puramente algébricas, relacionadas a números transcendentais, algumas das quais já conhecemos da matemática elementar, porém é necessário um aprofundamento do tema para o ambiente acadêmico, onde temos que lidar com análises mais detalhadas e complexas.
A integral da função algébrica  traz uma indefinição quando
traz uma indefinição quando  :
:

A existência desta indefinição nos leva a uma questão: Qual o procedimento para integrar a função:  ? A resposta é dada na análise numérica, calculando a integral pelos métodos de análise algébrica podemos chegar a seguinte conclusão:
? A resposta é dada na análise numérica, calculando a integral pelos métodos de análise algébrica podemos chegar a seguinte conclusão:

A função ln é chamada de logaritmo natural, a sua base é chamada de número de Euler, ele é um logarítmo conseqüente do cálculo da área sob a curva da função  , que pode ser obtido numericamente usando a integral de Riemann e outras técnicas de cálculo numérico. Aproximações deste número são possíveis utilizando-se técnicas de aproximações sucessivas com o uso de séries, discutidas em Cálculo (Volume 3).
, que pode ser obtido numericamente usando a integral de Riemann e outras técnicas de cálculo numérico. Aproximações deste número são possíveis utilizando-se técnicas de aproximações sucessivas com o uso de séries, discutidas em Cálculo (Volume 3).
Todos os teoremas para logaritmos, que estão incluidos nos cursos de nível médio, podem ser obtidos a partir da análise do logaritmo natural, também chamado de logaritmo Neperiano.
Vejamos os principais teoremas para os logaritmos:
Nas citações abaixo, consideremos  ,
,

Comprovação:
Da definição:


fazendo  e quando
e quando  :
:


O que comprova o teorema.

Comprovação:
Sendo  :
:


logo:


Comprovação:
Sendo:
 -> b vezes, que é:
-> b vezes, que é:
 -> b vezes, resultando:
-> b vezes, resultando:

Da definição do logarítmo natural e a partir do teorema fundamental do cálculo, podemos deduzir a derivada da função logarítmica natural, ou seja, se  que é a integral definida de
que é a integral definida de  , então a derivada é:
, então a derivada é:

Para integração de funções logarítmicas, veja o capítulo de técnicas de integração, para uma completa abordagem do tema.
A função  é chamada de função exponencial na base a, todas as funções exponenciais são introduzidas a partir da definição do logaritmo natural ln x como sua função inversa. As funções exponenciais são estas em que a parte variável é o logaritmo, ou seja:
é chamada de função exponencial na base a, todas as funções exponenciais são introduzidas a partir da definição do logaritmo natural ln x como sua função inversa. As funções exponenciais são estas em que a parte variável é o logaritmo, ou seja:
Se 
então:

O que implica  , tornando-o uma função, na qual podemos atribuir valores a x e obter uma imagem. O número a é chamado base, este número é facilmente identificado nos logaritmos convencionalmente abordados na matemática elementar, mas qual é a base da função
, tornando-o uma função, na qual podemos atribuir valores a x e obter uma imagem. O número a é chamado base, este número é facilmente identificado nos logaritmos convencionalmente abordados na matemática elementar, mas qual é a base da função  ?
?
Esta questão nos leva a um novo conceito abordado na próxima seção, o número de Euler.
A base do logarítmo natural é o número de Euler, simbolizado por: e, ele é obtido pela definição do logaritmo natural, esse número corresponde á área sob a curva da função:  , quando seu valor é unitário, ou seja:
, quando seu valor é unitário, ou seja:
 ,
,
mais formalmente:

O valor deste número pode ser encontrado por aproximação, utilizando-se os métodos de análise de seqûencias e séries, encontrados no livro: Cálculo (Volume 3).
A equação que fornece o valor do número de Euler é dada a seguir:

Nesta equação podemos observar que quanto mais alto o valor de n mais preciso se torna o valor de e.
De maneira simplificada, com base nos conceitos até agora abordados podemos encontrá-la da seguinte maneira:
Se  então
então  , logo:
, logo: 
Por outro lado, pela definição:

Para  :
:





Sendo:  e
e 
Concluimos que:

A maioria dos teoremas relacionados, têm origem nas conclusões obtidas no estudo do logarítmo natural, dos quais relacionamos os mais usados:
Seja a função  , pode-se afirmar que:
, pode-se afirmar que:

Comprovação:
Considerando:  e
e  ,
,


logo:


sendo:  e
e  ,
,

O que comprova o teorema.
De forma similar à análise anterior, sendo a função  , pode-se afirmar que:
, pode-se afirmar que:

Comprovação:
Considerando:  e
e  ,
,


logo:


sendo:  e
e  ,
,

O que comprova o teorema.
Seja a função  , pode-se afirmar que:
, pode-se afirmar que:

Comprovação:




O que comprova o teorema.
Consideremos que  , e conseqüentemente:
, e conseqüentemente:  , se derivarmos implicitamente este expressão:
, se derivarmos implicitamente este expressão:

Curiosamente, teremos:


Ou seja, a função exponencial natural é invariável durante o processo de derivação, o que traz uma série de implicações simplificadoras para estas funções.
Por outro lado se  , temos que:
, temos que:

Fazendo  e
e  , teremos:
, teremos:

Se  , concluimos que:
, concluimos que:

Que é adotada como uma derivada mais genérica, pois pode ser empregada em qualquer exponencial, pois inclui correção para o fator da base.
Como não poderia ser diferente, o valor da integral da função exponencial natural  é a própria função, conforme a regra da reversibilidade entre a derivada e a integral, apenas sendo necessária a devida observação da base, para eventual correção da diferencial e conseqüente introdução de fator de correção, nos casos em que a função torna-se composta.
é a própria função, conforme a regra da reversibilidade entre a derivada e a integral, apenas sendo necessária a devida observação da base, para eventual correção da diferencial e conseqüente introdução de fator de correção, nos casos em que a função torna-se composta.
Desta forma, temos:
 ,
,
Sendo C constante.
Como foi visto durante o ensino médio, os logaritmos têm uma definição direta e que denota a sua finalidade de expressar o valor do expoente em uma operação exponencial, a definição pura é dada da seguinte forma:
Se  então,
então,

Onde: a é chamada base do logaritmo, x é o logaritmando e n é o expoente.
O logaritmo é, portanto, a operação pela qual se obtém o expoente necessário para que a base seja elevada, numa operação exponencial e se obtenha o número x.
A função logarítmica de base a pode ser expressa da seguinte forma:

O que nos possibilita encontrar um valor para cada x expresso na equação.
Analisemos agora a possibilidade de encontrar uma função logarítmica de uma base a e transformá-la em uma função logarítmica de base natural, ou outra base qualquer:
Seja a função  , podemos dizer que:
, podemos dizer que:
 e que
e que  ,
,
como:  ,
,
 ,
,
 ,
,
 ,
,
O que nos possibilita afirmar que:
 ,
,
ou
 .
.
Note que a analogia serve para funções logarítmicas de qualquer base, visto que podemos substituir  por
por  sendo z a base que substituirá e na análise anterior.
sendo z a base que substituirá e na análise anterior.
O que nos possibilita considerar que quando temos duas bases, sejam: a e b, podemos promover a troca das bases, de forma que:

A derivada da função logarítmica com base diferente de e pode ser feita por substituição da base. Considerando  , temos que:
, temos que:
 ,
,
 ,
,
logo:



Que nos dá a derivada:

A trigonometria, tal qual vista na matemática elementar, está relacionada com as relações métricas do triângulo retângulo e do ciclo trigonométrico, agora introduziremos o estudo infinitesimal das funções trigonométricas que são largamente utilizadas nas ciências exatas.
Em um plano definido pelos eixos x e y podemos estabelecer coordenadas cartesianas para cada ponto, o que nos permite identificar cada um dos pontos em qualquer posição do plano, existe outra maneira de encontrar um ponto neste plano; se quisermos estabelecer uma relação triangular podemos determinar a posição de cada ponto no plano da seguinte forma:
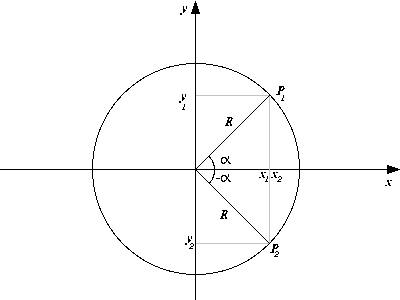
Figura 5
Imagine que cada ponto está numa distãncia R do ponto  em um plano cartesiano definido por pontos
em um plano cartesiano definido por pontos  , da mesma forma a reta R, que é definida entre os pontos
, da mesma forma a reta R, que é definida entre os pontos  , forma um ângulo com o eixo x, que chamaremos de
, forma um ângulo com o eixo x, que chamaremos de  , note que podemos identificar qualquer dos pontos no plano a partir de uma reta R e um ângulo
, note que podemos identificar qualquer dos pontos no plano a partir de uma reta R e um ângulo  .
.
Observemos que R, quando fixa, é uma reta que determina um conjunto de pontos em torno do ponto  , se fizermos
, se fizermos  variar em todos os valores possíveis teremos uma circunferência. Quando fazemos o valor de R variar teremos diferentes valores de x e y, porém a relação entre eles sempre será a mesma.
variar em todos os valores possíveis teremos uma circunferência. Quando fazemos o valor de R variar teremos diferentes valores de x e y, porém a relação entre eles sempre será a mesma.
Curiosamente, há uma relação entre o perímetro do círculo e o seu diâmetro, ela se apresenta constante qualquer que seja o raio do círculo; o resultado desta relação é um número transcedental chamado PI, representado pela letra grega de mesmo nome:  . Resgatando esta relação para a nossa análise podemos dizer que, se chamarmos o perímetro da circunferência, formada no gráfico, de
. Resgatando esta relação para a nossa análise podemos dizer que, se chamarmos o perímetro da circunferência, formada no gráfico, de  e admitirmos um diâmetro de
e admitirmos um diâmetro de  , então teremos:
, então teremos:

Que resulta em:

Que é uma relação bastante esclarecedora, visto que nos mostra uma dependência linear entre o raio e o comprimento de um fio imaginário que pudesse ser usado para seguir o contorno da circunferência do gráfico. Se o raio for unitário teremos um valor de referência para l, que poderá ser usado para encontrar qualquer comprimento de circunferência no gráfico, bastando para isto multiplicá-lo pelo raio, este valor de referência está ligado à circunferência fechada. Por outro lado, se fizermos com que R se desloque de um ângulo nulo, ou seja, que saia do eixo x em direção a y, formando um ângulo  , teremos pedaços de circunferência, que chamamos de arcos, considerando que temos um raio unitário e que percorremos um pedaço da circunferência para cada ângulo "
, teremos pedaços de circunferência, que chamamos de arcos, considerando que temos um raio unitário e que percorremos um pedaço da circunferência para cada ângulo " " que tomamos, temos uma correspondência entre ângulo e arco, ou seja: podemos nos referir a arcos como unidades de ângulos, esta unidade angular é chamada de Radiano. Qualquer círculo forma
" que tomamos, temos uma correspondência entre ângulo e arco, ou seja: podemos nos referir a arcos como unidades de ângulos, esta unidade angular é chamada de Radiano. Qualquer círculo forma  radianos e todas as relações entre os pontos da circunferência que o contorna e os eixos cartesianos podem ser referenciadas como relações entre partes desta medida.
radianos e todas as relações entre os pontos da circunferência que o contorna e os eixos cartesianos podem ser referenciadas como relações entre partes desta medida.
Como o radiano é uma medida real, isto nos leva a outra questão: O que determina o sinal negativo ou positivo neste valor?
Acontece uma variação destes valores quando nos deslocamos de um ponto a outro da circunferência, quando saimos do eixo x em direção ao ponto  o ângulo cresce, portanto temos que concluir que é positivo, recuando-o ao encontro do eixo x os valores diminuem, portanto se ultrapassarmos o eixo x o valor deve ser menor que zero, nos revelando um ângulo negativo.
o ângulo cresce, portanto temos que concluir que é positivo, recuando-o ao encontro do eixo x os valores diminuem, portanto se ultrapassarmos o eixo x o valor deve ser menor que zero, nos revelando um ângulo negativo.
Temos, portanto, uma circunferência dentro do plano cartesiano e seus pontos relacionados ao raio R e ao ângulo  , são referenciados pelas variáveis x e y no mesmo plano, agora imaginemos funções para que seja possível a partir do raio e do ângulo encontrar as variáveis, estas funções são o seno e o cosseno.
, são referenciados pelas variáveis x e y no mesmo plano, agora imaginemos funções para que seja possível a partir do raio e do ângulo encontrar as variáveis, estas funções são o seno e o cosseno.
A função seno, simbolizada como:

Nos dá o valor da variável y, ou seja, a altura do ponto em relação ao zero referencial, no encontro dos eixos, conforme espelhada no eixo y, quando o raio R é unitário, caso não seja fazemos  .
.
A função cosseno, simbolizada como:

Nos dá o valor da variável x, ou seja, a distância do ponto em relação ao zero referencial, no encontro dos eixos, conforme espelhada no eixo xquando o raio R é unitário, caso não seja fazemos  .
.
As funções seno e cosseno são periódicas, ou seja, pela natureza do ciclo trigonométrico, quando temos um valor em x maior que  temos a representação de um ciclo completo mais um ângulo residual, na verdade o valor representa este ângulo residual, o que nos leva a constatação que sempre será calculado o valor do seno ou cosseno do resto da operação
temos a representação de um ciclo completo mais um ângulo residual, na verdade o valor representa este ângulo residual, o que nos leva a constatação que sempre será calculado o valor do seno ou cosseno do resto da operação  quando um ângulo maior que
quando um ângulo maior que  for sugerido para x.
for sugerido para x.
Observações: Este livro utiliza a notação de funções trigonométricas da
lingua portuguesa, também é possível encontrar, em outros livros, as notações

ou

para representação de seno e cosseno respectivamente, utilizadas na língua inglesa.
Alguns valores de senos e cossenos de certos arcos são perfeitamente dedutíveis através da observação do ciclo, são eles:
Senos e cossenos notáveis
| Ângulo
|
0
|

|

|

|

|
0
|
1
|
0
|
-1
|

|
1
|
0
|
-1
|
0
|
Observando o gráfico podemos também concluir que o sinal do seno é idêntico ao sinal do ângulo, enquanto que o cosseno não acompanha o sinal do ângulo, de forma que cossenos de ângulos negativos são iguais a cossenos dos valores absolutos dos ângulos, ou seja:
sendo  ,
,

enquanto que:

Outros senos e cossenos podem ser obtidos pelas relações métricas no triângulo e são largamente utilizados, são:
Senos e cossenos mais comuns
| Ângulo
|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|

|
As equações desta seção são conseqüência das características dos senos e cossenos, seu comportamento cíclico e sua relação com uma circunferência de raio unitário lhes conferem uma excelente operatividade, possibilitando-nos fácil intercâmbio entre as mesmas.
As funções seno e cosseno estão relacionadas pela equação:

Comprovação:
Observando o ciclo trigonométrico, temos um triângulo cujos catetos são:  e
e  e sua hipotenusa é 1, portanto a identidade é conseqüente do conhecido teorema de Pitágoras.
e sua hipotenusa é 1, portanto a identidade é conseqüente do conhecido teorema de Pitágoras.
Sejam os ângulos a e b, o cosseno de sua soma é[1]:

Comprovação:
Nos pontos A e B do ciclo trigonométrico, temos os arcos para os ângulos a e b:
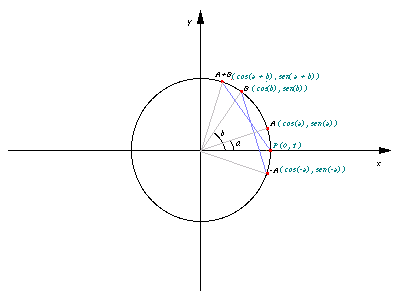
Figura 6
A distância entre os pontos P e (A+B) é igual à distância entre -A e B, o quadrado das duas é:
![{\displaystyle [\cos(a+b)-1]^{2}+sen^{2}(a+b)=[\cos(b)-\cos(-a)]^{2}+[\ {\mbox{sen}}(b)-\ {\mbox{sen}}(-a)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d04fcd4d09bab1f4c2c112b95fb157a88b5b37b2)
Da identidade básica:


![{\displaystyle -2\cos(a+b)+1+1=[cos^{2}(b)+sen^{2}(b)]-2\cos(-a)\cos(b)+[cos^{2}(-a)+sen^{2}(-a)]-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b840144aa4a86b8c5d3424fee8d1d141bd2f31e)



Como  e
e  :
:

O que comprova a identidade.
Sejam os ângulos a e b, o cosseno de sua diferença é[2]:

Comprovação:
Do cosseno da soma:

Substituindo b por -b:


O que comprova a identidade.
Se o ângulo a é  e b é x, então:
e b é x, então:


logo:

Por outro lado, se:
 e
e
 , obtemos:
, obtemos:

Sejam os ângulos a e b, o seno de sua soma é[3]:

Comprovação:
Sendo  e
e ![{\displaystyle \cos \left[{\frac {\pi }{2}}-(a+b)\right]=\ {\mbox{sen}}(a+b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd9f634ed48aa13591bf734a34c5b1ce59ef9069) , temos:
, temos:
![{\displaystyle \ {\mbox{sen}}(a+b)=\cos \left[{\frac {\pi }{2}}-(a+b)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8c5ab130bf7dded58488fc9cb3bbcd43efe11)
![{\displaystyle \ {\mbox{sen}}(a+b)=\cos \left[\left({\frac {\pi }{2}}-a\right)-b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abdf829b687311359cc480dc53fbc660b49b1ee1)


O que comprova a identidade.
Sejam os ângulos a e b, o seno de sua diferença é[1]:

Comprovação:
Se  ,
,
Substituindo b por -b, temos:

e  enquanto que
enquanto que  , logo:
, logo:

O que comprova a identidade.
Sejam os ângulos a e b, o produto de seus senos é[4]:
![{\displaystyle \ {\mbox{sen}}(a)\ {\mbox{sen}}(b)={\frac {1}{2}}\cdot [\cos(a-b)-\cos(a+b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb203fea1e1f845d38253c9c60193a53f9b8e36e)
Comprovação:
Considerando a identidade do cosseno da diferença de dois ângulos e subtraindo de cada um de seus membros os membros correspondentes da identidade do cosseno da soma de dois ângulos:

O que comprova a identidade.
Sejam os ângulos a e b, o produto de seus cossenos é[5]:
![{\displaystyle \cos(a)\cos(b)={\frac {1}{2}}\cdot [\cos(a+b)+\cos(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01b00d9444f433bda7933bad95f1af6e8bb43f0e)
Comprovação:
Considerando a identidade do cosseno da soma de dois ângulos e somando a cada um de seus membros os membros correspondentes da identidade do cosseno da diferença de dois ângulos:

O que comprova a identidade.
Sejam os ângulos a e b, o produto do seno de a pelo cosseno de b é[6]:
![{\displaystyle \ {\mbox{sen}}(a)\cos(b)={\frac {1}{2}}\cdot [\ {\mbox{sen}}(a+b)+\ {\mbox{sen}}(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc9c683868805fb4106f5b846ac35431f66f408b)
Comprovação:
Considerando a identidade do seno da soma de dois ângulos e somando a cada um de seus membros os membros correspondentes da identidade do seno da diferença de dois ângulos:

O que comprova a identidade.
Sejam os ângulos p e q, a soma dos senos de p e de q é:

Comprovação:
Podemos dizer que:

substituindo na identidade:

O que comprova a identidade.
Sejam os ângulos p e q, a soma dos cossenos de p e de q é:

Comprovação:
Seguindo a analogia anterior:

O que comprova a identidade.
Sejam os ângulos p e q, a diferença dos senos de p e de q é:

Comprovação:
substituindo q por -q em:

O que comprova a identidade.
Sejam os ângulos p e q, a diferença dos cossenos de p e de q é:

Comprovação:
substituimos q e q, por  e
e  em:
em:

O que comprova a identidade.
Precisaremos de um limite fundamental nas próximas seções, se trata de um limite que é utilizado na dedução das derivadas do seno e do cosseno, faremos sua dedução nesta seção. Considere o ciclo trigonométrico representado a seguir:

Figura 7
A figura 7 mostra a representação de um ângulo  no ciclo trigonométrico, o nosso propósito é deduzir o seguinte limite:
no ciclo trigonométrico, o nosso propósito é deduzir o seguinte limite:

Para isto, imagine o triângulo inscrito na circunferência, podemos dizer que o segmento de reta n é uma aproximação grosseira do arco  , porém observe que quando o ângulo se aproxima de zero o segmento se torna mais parecido com o respectivo ângulo, algébricamente podemos expressar que:
, porém observe que quando o ângulo se aproxima de zero o segmento se torna mais parecido com o respectivo ângulo, algébricamente podemos expressar que:

Por outro lado façamos o cálculo do valor do n; observando o triângulo podemos dizer que:
![{\displaystyle n^{2}=sen^{2}(\alpha )+[1-\cos(\alpha )]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3373441ef3dff5f42c31fa5b25e19b8f31153a25)
![{\displaystyle n^{2}=2[1-\cos(\alpha )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d864fba4442558a36fb56b3d458c3f59c07c04f1)
Logo:


Simplificando temos:
![{\displaystyle \ {\mbox{sen}}(\alpha )=n\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d61538f94bda9ad43f26de5f4b0aa74c0507fc)
Voltando para o nosso limite, temos que usar as nossas equações anteriores desta forma:
![{\displaystyle \left[\lim _{\alpha \to 0}{\frac {1}{\alpha }}=\lim _{n\to 0}{\frac {1}{n}}\right]\cdot \ {\mbox{sen}}(\alpha )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f496d310739c0d9038f0e35f221ff025ae85ab5)

Substituindo o valor do seno no lado da equação relaciondado ao n, teremos:
![{\displaystyle \lim _{\alpha \to 0}{\frac {\ {\mbox{sen}}(\alpha )}{\alpha }}=\lim _{n\to 0}\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c9815b44a77aa6c2d4d8f5b9af77100302398e5)
O que nos leva ao resultado:

A interpretação desse limite é a seguinte:
Uma vez que o ângulo diminui até valores próximos de zero e o arco tende a se assemelhar a uma reta em regiões próximas do zero, o valor do seno é igual ao valor do arco no limite, quando o seu valor se aproxima de ser nulo.
Agora podemos verificar qual a variação da função seno em relação ao seu ângulo, aplicando a definição da derivada ao seno, temos:


Aplicando o seno da soma:


Aplicando os limites:

Temos, então, o limite fundamental que é igual a 1, logo:

Também podemos verificar qual a variação da função cosseno em relação ao seu ângulo, aplicando a definição da derivada ao cosseno, temos:


Aplicando o seno da soma:


Aplicando os limites:

Novamente temos o limite fundamental, logo:

Como conseqüência do resultado da derivada do seno, podemos deduzir que a sua integral, como operação inversa é:

Cuja constante C é a constante devido a indefinição no processo de antidiferenciação, conforme já estudamos anteriormente.
Segundo o mesmo princípio colocado no caso da integral do seno, podemos afirmar que a operação de integração do cosseno é definida por:

Cuja constante C é a constante devido a indefinição no processo de antidiferenciação



















































































































































![{\displaystyle [\cos(a+b)-1]^{2}+sen^{2}(a+b)=[\cos(b)-\cos(-a)]^{2}+[\ {\mbox{sen}}(b)-\ {\mbox{sen}}(-a)]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d04fcd4d09bab1f4c2c112b95fb157a88b5b37b2)


![{\displaystyle -2\cos(a+b)+1+1=[cos^{2}(b)+sen^{2}(b)]-2\cos(-a)\cos(b)+[cos^{2}(-a)+sen^{2}(-a)]-2\ {\mbox{sen}}(-a)\ {\mbox{sen}}(b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3b840144aa4a86b8c5d3424fee8d1d141bd2f31e)












![{\displaystyle \cos \left[{\frac {\pi }{2}}-(a+b)\right]=\ {\mbox{sen}}(a+b)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fd9f634ed48aa13591bf734a34c5b1ce59ef9069)
![{\displaystyle \ {\mbox{sen}}(a+b)=\cos \left[{\frac {\pi }{2}}-(a+b)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d8c5ab130bf7dded58488fc9cb3bbcd43efe11)
![{\displaystyle \ {\mbox{sen}}(a+b)=\cos \left[\left({\frac {\pi }{2}}-a\right)-b\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abdf829b687311359cc480dc53fbc660b49b1ee1)





![{\displaystyle \ {\mbox{sen}}(a)\ {\mbox{sen}}(b)={\frac {1}{2}}\cdot [\cos(a-b)-\cos(a+b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/eb203fea1e1f845d38253c9c60193a53f9b8e36e)

![{\displaystyle \cos(a)\cos(b)={\frac {1}{2}}\cdot [\cos(a+b)+\cos(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/01b00d9444f433bda7933bad95f1af6e8bb43f0e)

![{\displaystyle \ {\mbox{sen}}(a)\cos(b)={\frac {1}{2}}\cdot [\ {\mbox{sen}}(a+b)+\ {\mbox{sen}}(a-b)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc9c683868805fb4106f5b846ac35431f66f408b)















![{\displaystyle n^{2}=sen^{2}(\alpha )+[1-\cos(\alpha )]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3373441ef3dff5f42c31fa5b25e19b8f31153a25)
![{\displaystyle n^{2}=2[1-\cos(\alpha )]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d864fba4442558a36fb56b3d458c3f59c07c04f1)


![{\displaystyle \ {\mbox{sen}}(\alpha )=n\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68d61538f94bda9ad43f26de5f4b0aa74c0507fc)
![{\displaystyle \left[\lim _{\alpha \to 0}{\frac {1}{\alpha }}=\lim _{n\to 0}{\frac {1}{n}}\right]\cdot \ {\mbox{sen}}(\alpha )}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f496d310739c0d9038f0e35f221ff025ae85ab5)

![{\displaystyle \lim _{\alpha \to 0}{\frac {\ {\mbox{sen}}(\alpha )}{\alpha }}=\lim _{n\to 0}\left[1-{\frac {n^{2}}{4}}\right]^{\frac {1}{2}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0c9815b44a77aa6c2d4d8f5b9af77100302398e5)














