Cálculo (Volume 2)/Geometria tridimensional
Coordenadas tridimensionais
[editar | editar código-fonte]Iniciando o nosso estudo de cálculo em três dimensões iremos nos concentrar nos sistemas de coordenadas cartesianas em três dimensões que é o estudo da geometria do nosso cotidiano. Este estudo inicia com conceitos básicos e depois se aprofunda em conceitos introdutórios sobre algebra linear, porém com uma ênfase maior à geometria ao invés da abstração comum no curso de álgebra linear.
Introduziremos agora os conceitos de localização de pontos nos sistemas tridimensionais:
Vetores
[editar | editar código-fonte]No esforço em representar quantidades, o homem criou os números, porém lhes falta algo fundamental: a propriedade de indicar evolução, tendência e forma, quando dizemos que temos 5 objetos, para uma noção de volume e quantidade isto é o bastante, porém quando dizemos que a velocidade de um veículo é 70 km/h, isto é apenas suficiente para uma análise quantitativa e não nos fornece meios de avaliar o comportamento do veículo em sua trajetória.
A evolução da noção de representação matemática de eventos no espaço trouxe a necessidade de expressá-los de uma forma que fornecesse uma noção mais ampla do que a de quantidade, para isto foi criado um novo ente matemático chamado vetor. Um vetor é a representação das características espaciais e evolutivas de um elemento, com ele podemos avaliar mais que a quantidade de elementos, podemos analisar o comportamento destes elementos.
Introduziremos, agora, uma noção multidimensional de vetores, mais dedicada a vetores no espaço em três dimensões, este estudo é fundamentalmente importante para análises mais complexas do cálculo. A abordagem de muitos problemas sob a perspectiva vetorial simplifica muito as análises de problemas no espaço.
Para uma melhor compreesão subdividimos o estudo em dois tópicos:
Retas
[editar | editar código-fonte]Neste momento temos como desenvolver um conceito de reta diferente do que estávamos habituados, a noção de forma paramétrica em conjunção com a definição vetorial nos dá a possibilidade de descrever uma reta em termos vetoriais paramétricos. Uma definição da reta, concebida em termos vetoriais, é feita a partir dos dois vetores que determinam os pontos no espaço por onde a reta passa.
Equações da reta
[editar | editar código-fonte]Observemos o gráfico:
O vetor é, simplesmente, a representação de um segmento de reta cujo ponto inicial é a orígem do sistema de coordenadas, se somarmos um segundo vetor ao que temos, isto resultará em um segmento de reta cujo ponto inicial é o segundo vetor que tomamos. Partindo deste pricípio, se temos dois pontos temos dois vetores, ao subtrairmos os dois vetores teremos um vetor na orígem, paralelo ao segmento de reta por onde passam os dois pontos. Uma vez que o primeiro ponto é um vetor, teremos a representação deste segmento de reta se somarmos o primeiro vetor ao vetor paralelo à reta. Algebricamente temos:
Se são dois pontos e é o vetor que se origina dos dois pontos...
Por outro lado, se fizermos com que o lado da equação onde está o vetor aumente ou diminua de valor, de acordo com a variação de um parâmetro, teremos um valor variável de dentro da mesma reta:
Então, teremos a equação da referida reta. Como os pontos podem ser representados sob a forma de vetores, podemos definir a reta tal que:
Três equações paramétricas espaciais podem ser obtidas desta equação vetorial, é notável que cada eixo deverá ter uma definição de sua variável para cada valor do parâmetro, logo façamos a dedução destas equações:
De onde temos as equações paramétricas:
Do mesmo modo ao eliminarmos o parâmetro encontramos a relação fundamental entre todos os eixos, o que pode ser bastante útil em certos cálculos onde precisamos estabelecer uma relação entre variáveis sem considerar o parâmetro:
Relacionando duas retas
[editar | editar código-fonte]Uma vez que definimos as equações da reta: vetorial, paramétrica e simétrica... Podemos agora encontrar relações entre duas retas no espaço. De modo geral, temos três condições nas quais podemos relacionar duas retas no espaço, estas podem ser paralelas, reversas ou concorrentes.
- Paralelas:
- São duas ou mais retas que mantém uma distância constante entre seus pontos, ou seja, as mesmas estão na mesma direção;
- Reversas:
- São duas ou mais retas que não estão na mesma direção, porém não se encontram em nenhum ponto do espaço;
- Concorrentes:
- São duas ou mais retas que se encontram em algum ponto do espaço.
Planos
[editar | editar código-fonte]A definição de um plano no espaço pode ser obtida através de um conceito vetorial da mesma forma que o fizemos quando vimos a reta. Para isto devemos estabelecer o que é necessário para que um plano seja perfeitamente definido. Se imaginarmos uma reta no espaço podemos perceber que diversos planos passam pela mesma, na verdade, todas as direções perpendiculares à da reta fornecem um plano possível, nos resta escolher uma destas direções para estabelecer o plano. Pensando em um vetor direção que nos forneça as características necessárias para representar a reta, temos que ter em mente um segundo vetor que defina qual dos planos que passam pela reta será escolhido.
Equação do plano
[editar | editar código-fonte]A equação do plano deve refletir a seguinte verdade:
Dados dois vetores em , sendo os dois perpendiculares entre sí, então:
O que nos leva a definir um dos vetores como a diferença entre dois vetores posição, originados no sistema de eixos:
logo,
Sendo:
- ;
temos,
Consideremos vetor referência, visto que é o vetor do ponto de origem do vetor que projetamos no plano, da mesma forma que é referência visto que define a direção do plano, ambos podem ser constantes, logo teremos:
Onde podemos definir:
Portanto a equação algébrica de um plano no espaço pode ser definida como:
Onde o vetor é o vetor variável, correspondente a posição do ponto sobre o plano, enquanto que e são constantes que definem o plano. Para esta notação chamamos de normal do plano, pois representa um segmento de reta perpendicular a direção do plano, enquanto que chamamos de escalar de referência, uma vez que o mesmo determina o referencial para o plano no sistema dos eixos ordenados.
Pontos no plano
[editar | editar código-fonte]Suponhamos que temos um conjunto de pontos no espaço e desejemos encontrar o plano ao qual estes pertencem, que critérios teremos que usar para determinar uma regra de inclusão dos mesmos em um plano? A resposta está no critério de coplanaridade, para determinar este devemos saber qual o número mínimo de pontos para definir um plano no espaço. Para determinar a normal precisamos de dois vetores no espaço, uma vez que precisamos de no mínimo três pontos para determinar dois vetores no espaço, precisamos de três pontos para determinar um plano. Agora imaginemos que temos mais de três pontos, como saberemos se todos pertencem ao mesmo plano? Simplesmente agrupamos três e calculamos o plano, e depois usamos a equação do plano para verificar se os demais petencem ao mesmo plano.
Tomemos os pontos como base do plano, o que nos faz definir os vetores:
O que define um vetor normal:
Uma vez que o ponto está em outro segmento de reta, diferente dos demais pontos no diagrama, precisamos determinar se o mesmo pertence ao plano formado pelos vetores que definimos anteriormente, para isto encontremos o vetor para o segmento de reta onde o mesmo está localizado:
E depois, poderemos substituir os vetores na equação do plano:
Donde podemos verificar se é verdadeira para os valores correntes dos vetores em qualquer situação... O método, em geral, faz o cálculo do produto misto, visando encontar vetores que o anulam.
Exemplo - plano dos pontos
[editar | editar código-fonte]Sejam os pontos , determinemos o plano determinado pelos pontos...
Escolhemos um ponto como orígem, encontrando os vetores relacionados aos outros dois pontos:
Suponha como orígem, temos os vetores:
Com os vetores encontramos a normal do plano através do produto vetorial dos mesmos:
O plano é definido pela equação:
A parte que depende do ponto origem , é:
que resulta em:
Interseção entre planos
[editar | editar código-fonte]Sejam os planos:
e
,
Onde definimos os vetores posição:
e os vetores normais:
Analisando a simetria, podemos concluir que o resultado da interseção entre dois planos é uma reta, sendo a mesma, perpendicular aos vetores normais dos dois planos simultaneamente. Considerando a característica de perpendicularidade do produto vetorial, podemos fazer:
Donde obtemos:
Devemos encontrar um ponto da reta, para que possamos definir a mesma em termos paramétricos e simétricos, usualmente podemos definir a variável e encontrar o ponto:
Se , teremos:
e
,
Observe que usamos variáveis sem índice, visto que os pontos são os mesmos, quando se define a reta.
O que nos fornece:
,
o que nos dá um plano em . A reta intercepta o plano em:
Definamos agora o valor de ,
Simplificando , temos:
e o ponto é:
Bastando-nos aplicá-lo à equação vetorial da reta para encontrá-la:
Exemplo - Reta em dois planos
[editar | editar código-fonte]Sejam os planos , devemos encontrar a reta resultante da interseção dos dois planos.
Primeiro, extraímos os vetores normais dos planos:
- ;
- ;
Com estes vetores podemos encontrar o vetor diretor da reta, que é perpendicular à normal de ambos:
Agora, devemos encontrar um ponto da reta:
Supomos em ambos os planos,
e
sendo o ponto:
Substituimos os valores na equação da reta,
ou
Distância entre ponto e plano
[editar | editar código-fonte]Suponhamos que um ponto qualquer no espaço: esteja localizado a uma certa distância de um plano, cuja equação que o define é: , cujo vetor normal é: . Como já é de nosso conhecimento, o plano impõe uma distância para o ponto que varia de acordo com a distância da coordenada usada como referência para a medida, portanto, não faz sentido definirmos a distância entre o plano e um ponto se não definirmos este ponto como o mais próximo do plano, o que implica o cálculo da projeção do vetor distância do ponto sobre o vetor normal do plano.
Definimos a distäncia entre o plano e um ponto arbitrário como a menor distância entre este e o plano, denominando-a de . Pelo produto escalar obtemos:
Ou seja,
Que nos dá a equação:
Porém, para o vetor definimos a distância entre o ponto no plano e o seu par, que é reflexo do ponto nos eixos:
Onde é um ponto qualquer no plano.
Ou seja,
Que substituimos na equação da distância entre plano e ponto acima:
Temos o escalar semelhante a equação do plano, o que nos dá
Podemos adotar uma nomenclatura mais conveniente se usarmos o vetor normal do plano definido como: :
O que define a distância entre o plano e o ponto.
Exemplo - Distância entre dois planos
[editar | editar código-fonte]Sejam dois planos paralelos: e , encontremos a distância entre os dois planos:
Como os dois planos são paralelos podemos encontrar um ponto em um dos planos, depois utilizar a equação anterior para encontrar a distância entre os dois planos:
Definamos e temos o ponto em um dos planos:
,
para o primeiro plano apresentado.
Agora, basta-nos substituir os valores na equação:
temos:
e
A distância é:
Superfícies simples
[editar | editar código-fonte]Superfícies são conjuntos de pontos no espaço cujo comportamento e aparência se assemelham aos planos. Uma superfície tem a aparência de uma folha de material flexível que assume curvas de acordo com a função que a representa, embora a mesma não seja flexível e mantenha a sua forma no espaço aparentemente rígida. De fato, uma superfície é como uma lâmina que mantém a sua forma depois que é moldada.
Com o estudo de superfícies simples teremos melhores condições de analisar estruturas de superfícies mais complexas.
Superfícies cilíndricas
[editar | editar código-fonte]Cilindro, não é a definição de um elemento de base circular e altura definida, na verdade a noção de cilindro é algo mais universal... Qualquer elemento formado por retas paralelas delimitando uma certa região no espaço pode ser chamado de cilindro. Uma superfície cilíndrica é uma membrana formada por infinitas retas paralelas em torno de uma região do espaço, estas retas são chamadas de geratrizes.
Um cilindro circular convencional pode ser algebricamente concebido sob a forma:
Onde são as variáveis e é uma constante que define o raio da base do cilindro. Você deve achar estranho que isto se pareça com a equação de uma circunferência, porém, de fato, esta é uma circunferência em um gráfico de duas dimensões e um cilindro circular em outro de três dimensões.
Em um sistema de três dimensões definimos três variaveis, visto que a variável não está definida na equação acima, temos que admitir que qualquer ponto do eixo pertence ao gráfico definido pela equação acima, ou seja, para cada ponto definido no plano existe um conjunto de pontos paralelo ao eixo , o que define uma de reta paralela ao eixo z e, imediatamente, um conjunto de retas paralelas a este eixo, uma para cada ponto do plano .
Por estes motivos, o gráfico gerado pela equação acima é:

|
Cilindro circular gerado a partir da equação acima. |
Este também pode ser considerado um cilindro elíptico, uma vez que podemos tomar dois valores de eixos para a abertura do mesmo.
Outro exemplo de cilindro, segundo este conceito é o parabólico:

|
Cilindro parabólico gerado a partir de uma equação na forma . |
E, finalmente podemos apresentar um cilindro hiperbólico:

|
Cilindro hiperbólico gerado a partir de uma equação na forma . |
Superfícies quadrátricas
[editar | editar código-fonte]Uma superfície quadrática é um conjuntos de pontos no espaço gerados por uma equação puramente quadrática, de modo geral uma equação deste tipo é escrita da seguinte forma:
Onde são constantes, e pelo menos um de A,B,C,D,E e F não é nulo.
As quadráticas são representações tridimensionais das cônicas, a evolução do modelo quadrático para o universo tridimensional é representada sob a forma de novas curvas resultantes da fusão de duas ou mais cônicas.
De forma geral, podemos estabelecer um modelo simplificado quando levamos em conta os parâmetros de vértices e centro das cônicas, desta forma podemos substituir a equação acima, através de translações e rotações, pelas formas:
Traços
[editar | editar código-fonte]Como vimos na seção sobre superfícies cilíndricas, logo acima, quando uma das variáveis é eliminada podemos analisar a equação resultante e definir a curva que será projetada sobre o plano formado pelas duas variáveis restantes na equação. Quando analisamos uma equação quadrática, as formas se modificam para cada plano que tomamos, por isto devemos adotar os planos dos eixos para verificar qual a forma que a equação determina sobre os mesmos. Podemos fazer e teremos um plano , por exemplo; ou seja, podemos eliminar cada uma das variáveis da equação e analisar a equação apenas com as restantes. A imagem da projeção da equação em apenas um plano em particular é chamada de traço da curva para o plano.
Observemos o gráfico abaixo:
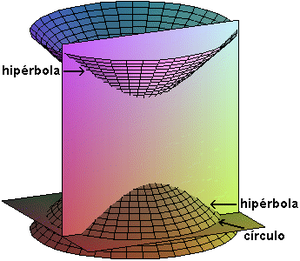
|
Dois traços em um hiperbolóide de duas folhas. Observe que em cada plano um componente básico é formado, na vetical temos uma hipérbole, enquanto que na horizontal temos círculos, ou elipses. |
Os traços podem ser usados para formação das perspectivas das superfícies para valores relevantes da equação, de forma a nos fornecer um esboço de sua aparência... Façamos a análise da equação do hiperbolóide:
Podemos verificar qual o traço do plano fazendo: , o que nos dá a equação:
Considerando que temos resultados possíveis quando:
O artifício não se mostra eficaz para a análise...
Podemos substituir a parte na equação inicial por uma variável que nos permita analisar em quais condições é possível encontrar raízes para a equação do traço, para isto fazemos:
Neste caso, teremos que verificar quando:
O que nos fornece a constatação algébrica sobre o que já é possível observar no gráfico, ou seja, que existe um espaço no eixo onde não existem elipses, o que se deve aos pontos de indefinição existentes na hipérbole.
As áreas onde as raízes existem nos revelam circunferências se , ou elipses no caso contrário, isto é o que aparece no traço horizontal da equação.
Agora, ao verificar qual o traço do plano fazendo: , temos a equação:
O que é uma hipérbole.
Formas comuns
[editar | editar código-fonte]As formas quadráticas mais comuns estão representadas na tabela abaixo, os seis tipos básicos podem ser classificados pela semelhança de suas formas com as cônicas, que já abordamos anteriormente. Dizemos que um sólido obtido pela evolução de uma cônica no espaço recebe o nome da mesma mais o sufixo "óide" para indicar que há parentesco entre estas, facilitando a identificação da família de curvas à qual esta pertence.























































































































































