Matemática divertida/Triângulo de Pascal

O Triângulo de Pascal

O triângulo de Pascal são números dispostos desta maneira:

$1$

$1\quad 1$

$1\quad 2\quad 1$

$1\quad 3\quad 3\quad 1$

$1\quad 4\quad 6\quad 4\quad 1$

$1\quad 5\quad 10\quad 10\quad 5\quad 1$

$1\quad 6\quad 15\quad 20\quad 15\quad 6\quad 1$

$1\quad 7\quad 21\quad 35\quad 35\quad 21\quad 7\quad 1$

$1\quad 8\quad 28\quad 56\quad 70\quad 56\quad 28\quad 8\quad 1$

O triângulo de Yang Hui.

O triângulo aritmético é conhecido há muito tempo, mas recebeu o nome de 'Triângulo de Pascal' devido aos estudos que o filósofo e matemático Blaise Pascal (1623-1662) fez deste.

O triângulo é infinito e simétrico, e seus lados esquerdo e direito sempre devem possuir o número $1.$ Cada linha possui um número a mais que a linha anterior. Além disso, o triângulo também possui várias propriedades interessantes que permitem construir com facilidade a linha seguinte. Vamos detalhar estas propriedades a seguir.

Propriedades

Propriedade 1

A primeira propriedade do triângulo que iremos apresentar está relacionada à soma dos elementos de cada uma das linhas. Para ilustrar isto, vamos associar a cada linha do triângulo um número, começando do $0:$

A propriedade diz que a soma de todos os números de uma linha é igual a $2$ elevado àquele número que associamos à linha. E o que significa isto?

Quando dizemos que o número $2$ está elevado a $3,$ por exemplo, queremos dizer que o $2$ foi multiplicado por si mesmo $3$ vezes:

$2^{3}=\underbrace {2\times 2\times 2} _{3\mathrm {vezes} }=8$

Você pode observar na figura o resultado das somas relacionadas à cada linha do triângulo:

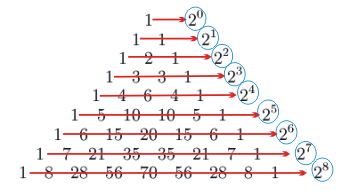
Vamos conferir algumas delas:

• $2^{0}=1$ (qualquer número elevado a $0$ dá $1$)
• $1+1=2=2^{1}$
• $1+2+1=4=2\times 2=2^{2}$
• $1+3+3+1=8=2\times 2\times 2=2^{3}$
• $1+4+6+4+1=16=2\times 2\times 2\times 2=2^{4}$
• $1+5+10+10+5+1=32=2\times 2\times 2\times 2\times 2=2^{5}$

E assim você mesmo pode continuar a verificar a propriedade.

Propriedade 2

A próxima propriedade do triângulo que veremos é a relação de Stifel.

Ela diz que a soma de dois números de uma mesma linha do triângulo é o número que está na linha logo abaixo, bem abaixo dos dois números somados. A figura ilustra melhor a propriedade:

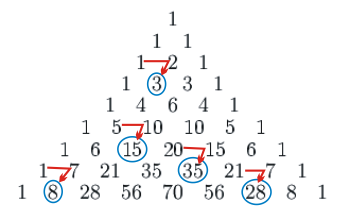
Vamos verificar as somas apontadas na figura:

$1+2=3$

$1+7=8$

$5+10=15$

$20+15=35$

$21+7=28$

Você pode continuar verificando essa propriedade calculando mais somas.

Propriedade 3

Nossa próxima propriedade diz respeito à soma dos números dispostos em diagonal, começando sempre do $1$ a partir da direita. Observe a figura para visualizar melhor:

A soma dos números da coluna estará sempre na coluna seguinte, na linha logo abaixo daquela em que está o último número que foi somado, como mostra a figura.

Vamos conferir algumas somas:

$1+1+1+1+1=5$

$1+3+6=10$

$1+3+6+10+15=35$

$1+6+21=28$

Da mesma forma que foi feito com as propriedades anteriores, você pode continuar verificando esta! Mas tome cuidado, as somas das colunas devem começar sempre a partir do primeiro número $1$ da coluna.

Propriedade 4

Nossa última propriedade é bem parecida com a anterior, só que, em vez de as somas começarem do lado direito do triângulo, desta vez devem começar do lado esquerdo:

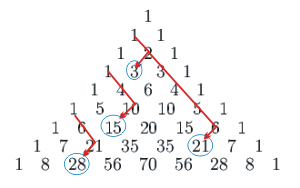
Da mesma forma, você vai encontrar a soma desta diagonal na linha abaixo daquela em que está o último número somado. Também aqui você deve ter sempre o cuidado de começar a soma do primeiro número $1$ da coluna.

Vamos verificar as somas da figura:

$1+2=3$

$1+2+3+4+5+6=21$

$1+4+10=15$

$1+6+21=28$

Continue verificando a propriedade!

Exercício

1. No triângulo de Pascal abaixo, faltam os números de algumas linhas. Utilize as propriedades que vimos acima para completar corretamente os espaços. Procure usar mais de uma propriedade para encontrar os números que faltam. As respostas você encontra nesta página.

$1$

$1\quad 1$

$1\quad 2\quad 1$

$1\quad 3\quad 3\quad 1$

$1\quad 4\quad 6\quad 4\quad 1$

$1\quad 5\quad 10\quad 10\quad 5\quad 1$

$1\quad 6\quad 15\quad 20\quad 15\quad 6\quad 1$

$1\quad 7\quad 21\quad 35\quad 35\quad 21\quad 7\quad 1$

$1\quad 8\quad 28\quad 56\quad 70\quad 56\quad 28\quad 8\quad 1$

$1\quad {\color {Blue}\Box }\,\quad 36\quad 84\quad {\color {Blue}\Box }\,\,\quad {\color {Blue}\Box }\quad 84\,\,\quad 36\quad {\color {Blue}\Box }\quad 1$

$1\quad 10\quad {\color {Blue}\Box }\quad 120\quad {\color {Blue}\Box }\quad 252\quad {\color {Blue}\Box }\quad 120\quad {\color {Blue}\Box }\quad 10\quad 1$

$1\,\,\quad {\color {Blue}\Box }\quad 55\quad {\color {Blue}\Box }\quad 330\quad {\color {Blue}\Box }\,\,\quad {\color {Blue}\Box }\quad 330\quad {\color {Blue}\Box }\quad 55\quad {\color {Blue}\Box }\,\,\quad 1$

2. Usando as doze linhas do triângulo de pascal obtido no exercício anterior, destaque todos os números pares que encontrar, circulando cada um deles. Curiosamente, a disposição dos números pares deste triângulo segue um padrão. Consegue identificá-lo? Dicas: tente completar mais algumas linhas do triângulo e consulte a próxima seção deste wikilivro.