Lógica/Lógica Tradicional/O Silogismo
O Silogismo Categórico
[editar | editar código-fonte]- Silogismo Categórico é uma forma de raciocínio lógico na qual há duas premissas e uma conclusão distinta destas premissas, sendo todas proposições categóricas ou singulares.
- Termo Médio é o termo que se repete nas duas premissas mas não aparece na conclusão. Por exemplo:
- Todo cachorro é mamífero.
- Todo mamífero é vertebrado.
- Logo todo cachorro é vertebrado.
- Neste caso, o termo médio é "mamífero"
Regras do silogismo
[editar | editar código-fonte]A validade de um silogismo depende do respeito às regras de estruturação. Tais regras, em número de oito, permitem verificar a correção ou incorreção do silogismo. As quatro primeiras regras são referentes aos termos e as quatro últimas são referentes às premissas. São elas:
- 1) Todo silogismo contém somente três termos: maior, médio e menor;
- 2) Os termos da conclusão não podem ter extensão maior que os termos das premissas;
- 3) O termo médio não pode entrar na conclusão;
- 4) O termo médio deve ser universal ao menos uma vez;
- 5) De duas premissas negativas, nada se conclui;
- 6) De duas premissas afirmativas não pode haver conclusão negativa;
- 7) A conclusão segue sempre a premissa mais fraca;
- 8) De duas premissas particulares, nada se conclui.
Aplicando Diagramas de Venn à resolução de silogismos
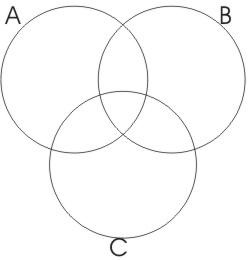
[editar | editar código-fonte]- O primeiro passo é representar os três termos do silogismo da seguinte forma:
- Assim representaremos quatro subconjuntos para cada conjunto:
- Então são eliminados os conjuntos que estão em desacordo com as premissas. Digamos que temos as seguintes premissas:
- Todo A é B.
- Todo B é C.
- Ora, se todo A é B, então devemos eliminar os subconjuntos dos As que não são Bs:
- E se todos Bs são Cs, devemos eliminar os subconjuntos dos Bs que não são Cs:
- Restaram apenas três subconjuntos. Mas como as premissas não informam sobre os Cs que não são Bs ou As, devemos ignorar estes subconjuntos. Resta apenas os conjuntos dos As que são Bs e também são Cs. Portanto, a conclusão é: Todo A é C.
Diagrama de duas premissas que não permitem construir um silogismo válido
[editar | editar código-fonte]- Se termo médio repetir-se no predicado de duas premissas tipo A desta forma:
- Todo A é C.
- Todo B é C.
- O diagrama ficará assim:
- As premissas não informam sobre os subconjuntos de C. Portanto, não é possível formular um silogismo logicamente válido com duas premissas universais afirmativas com o termo médio distribuído no predicado das duas.
Diagrama para Universal Negativa
[editar | editar código-fonte]- Agora vejamos um raciocínio que contenha uma premissa universal negativa:
- Todo A é B.
- Nenhum B é C.
- Já vimos como lidar com a primeira premissa:
- Quanto à segunda premissa, se nenhum B é C, então devemos eliminar os subconjuntos dos Bs que são Cs:
- Podemos ver que A e C não tem subconjuntos em comum. Como nenhuma premissa isoladamente estabelece qualquer relação com A e C, podemos concluir que “Nenhum A é C”:
Diagrama de duas premissas Universais Negativas
[editar | editar código-fonte]- Agora vejamos como seria se houvesse duas premissas negativas, por exemplo:
- Nenhum A é B.
- Nenhum B é C.
- Não teríamos informação sobre a existência de As que não são Cs, de Cs que não são As nem de As que são Cs. Por isto não é possível um silogismo com duas premissas negativas.
Diagrama para Particular Afirmativa
[editar | editar código-fonte]- Agora vejamos como fica um silogismo com uma premissa particular afirmativa, digamos:
- Todo A é B.
- Alguns Cs são As.
- Já sabemos como lidar com a primeira premissa. Quanto à segunda, se alguns Cs são As, então o conjunto C tem ao menos um subconjunto em comum com A:
- Como, dadas as premissas, podemos ter certeza que existem As que são Bs e também são Cs, e como nenhuma premissa isoladamente estabelecia qualquer relação entre B e C, podemos concluir que alguns Bs são Cs:
- Repare que a premissa “Alguns Cs são As” informa que C tem ao menos um – se não dois – subconjuntos em comum com A. Porém, ela isoladamente não nos permite determinar quais são. Nós pudemos dizer que existem As que são Bs e também são Cs, pois a premissa “Todo A é B” elimina os As que são Cs e não são Bs. Portanto, não é possível um silogismo com duas premissas particulares.
Diagrama para Particular Negativa
[editar | editar código-fonte]- Agora vejamos como lidar com silogismos que tenham uma premissa particular negativa, tal como:
- Todo A é B.
- Alguns Cs não são Bs.
- É de se esperar que a essa altura já saibamos como lidar com a primeira premissa. Quanto à segunda, repare que segundo ela existem Bs que não são Cs, mas ela isolada não nos permitiria determinar se existem Cs que são As mas não são Bs, ou se existem Cs que não são As e também não são Bs. Poderia haver somente um destes casos ou ambos. Mas a primeira premissa, “Todo A é B”, elimina os Cs que não As mas não são Bs. Isto nos permite determinar que, segundo as premissas, existem Cs que não são As e também não são Bs:
- Como não há premissas neste silogismo que isoladas estabelecem relação entre A e C, podemos concluir que alguns Cs não são As:
Diagrama de silogismos que requerem a assunção de existência do termo médio
[editar | editar código-fonte]- Em alguns casos, um silogismo só é valido se supormos a existência do termo médio. É como se houvesse uma terceira premissa: "X existe", onde "X" é o termo médio.
- Veja por exemplo o silogismo Darapti, no qual as premissas são "todo A é B" e "todo A é C":
- Não podemos concluir coisa alguma. Contudo, assumindo a existência do termo médio "A", veja como fica:
Lista de silogismos categóricos válidos
[editar | editar código-fonte]- Os nomes dos silogismos foram dados na Idade Média com o intuito de facilitar a memorização. As vogais dos nomes são as mesmas vogais usadas para designar as proposições. Exemplo: O silogismo BARBARA contém três Universais Afirmativas (A).
Figura 1
[editar | editar código-fonte]- O termo médio ocupa a posição de sujeito na premissa maior e predicado na premissa menor.
- Barbara
Todo B é um A.
Todo C é um B.
∴ Todo C é um A.
- Celarent
Nenhum B é um A.
Todo C é um B.
∴ Nenhum C é um A.
- Darii
Todo B é um A.
Alguns Cs são Bs.
∴ Alguns Cs são As.
- Ferio
Nenhum B é um A.
Alguns Cs são Bs.
∴ Alguns Cs não são As.
Figura 2
[editar | editar código-fonte]- O termo médio ocupa a posição de predicado em ambas as premissas.
- Cesare
Nenhum B é um A.
Todo C é um A.
∴ Nenhum C é um B.
- Camestres
Todo B é um A.
Nenhum C é um A.
∴ Nenhum C é um B.
- Festino
Nenhum B é um A.
Alguns Cs são As.
∴ Alguns Cs não são Bs.
- Baroco
Todo B é um A.
Alguns Cs não são As.
∴ Alguns Cs não são Bs.
Figura 3
[editar | editar código-fonte]- O termo médio ocupa a posição de sujeito nas duas premissas.
- Darapti
Todo C é um A.
Todo C é um B.
∴ Alguns Bs são As.
- Esta forma requer a assunção de que alguns Cs existem.
- Datéi
Todo C é um A.
Alguns Cs são Bs.
∴ Alguns Bs são As.
- Déamé
Alguns Cs são As.
Todo C é um B.
∴ Alguns Bs são As.
- Felapton
Nenhum C é um A.
Todo C é um B.
∴ Alguns Bs não são As.
- Esta forma requer a assunção de que alguns Cs existem.
- Feréon
Nenhum C é um A.
Alguns Cs são Bs.
∴ Alguns Bs não são As.
- Bocardo
Alguns Cs não são As.
Todo C é a B.
∴ Alguns Bs não são As.