Iniciação à Pesquisa Científica em Saúde /REPOSITÓRIO DE EXERCÍCIOS RESOLVIDOS/ Exercício 14: Hipertensão arterial em gestantes I
Questão 14: Hipertensão arterial em gestantes I
[editar | editar código-fonte]Para realizar um estudo sobre hipertensão arterial na gravidez, 86 mulheres gestantes hipertensas e normotensas foram aleatoriamente selecionadas. Na Tabela a seguir, características clínicas forma comparadas entre os grupos
| Tabela 1 - Características clínicas das grávidas incluídas no estudo | |||
|---|---|---|---|
| Hipertensas (n=61) | Normotensas (n=25) | p | |
| Pressão arterial média (DP), mmHg | 133,8 (17,7) | 89,6 (9,6) | <0,001 |
| Hipertensão arterial prévia | 22 (36,1%) | ... | |
| Uso de vasodilatadores | 32 (52,5%) | ... | |
| Idade materna (DP), anos | 27,5 (6,1) | 28,9 (6,1) | 0,07 (NS) |
| Raça branca | 17 | 6 | |
| Raça não branca | 46 | 19 | 0,74 (NS) |
| Idade gestacional (DP), semanas | 34,5 (3,5) | 36,5 (3,9) | 0,06 (NS) |
| S: significativo, p<0,05. NS: não significativo. DP: desvio padrão | |||
a) Existe diferença significativa entre os valores da pressão arterial media das gestantes normotensas e hipertensas?
b) Formule o teste de hipóteses para a variável idade materna. Analise o p-valor e compare as idades em função do resultado do teste
c) Houve associação entre raça branca ou não branca e a ocorrência de hipertensão arterial?
Resposta da questão:
[editar | editar código-fonte]a) Resposta: A diferença entre a pressão arterial média das gestantes normotensas e hipertensas foi significativa, uma vez que p-value<α.
Justificativa: Um resultado estatisticamente significativo deve ser interpretado como a rejeição da hipótese nula Ho (que os valores médios da pressão são iguais no grupo de hipertensas e normotensas). Neste caso, a Ho seria: “a pressão arterial média é igual entre as gestantes hipertensas e normotensas”. Para sabermos se vamos ou não rejeitá-la, precisamos de mais outros dois valores:
Escolher um nível de significância para o teste (α): é a probabilidade de se cometer erro tipo I (rejeitar a hipótese nula quando esta for verdadeira). Ou seja, é o erro máximo que se está disposto a aceitar. Ele é estabelecido arbitrariamente. Neste caso, adotou-se α=5%.
Verificar se os pressupostos para o teste escolhido foram atendidos: para se utilizar o teste-t de médias para amostras independentes é preciso que as variáveis sejam numéricas e que apresentem distribuição normal (ou que tende para normal) nos subgrupos analisados (hipertensas e normotensas). Além disto as amostras precisam ser independentes, ou seja, a gestante só faz faz parte de um dos grupos (ou é normotensa ou é hipertensa). O verdadeiro valor do desvio-padrão populacional é desconhecido (sigma).
Calcula-se a estatística do teste e o p-valor correspondente: é a probabilidade calculada de se obter os dados observados se a Ho for verdadeira, ou seja, é a probabilidade de ter sido ao acaso. Neste caso, o valor de p encontrado foi <0,001.
Se p-value < α, descartamos a hipótese nula e o resultado é estatisticamente significante. Porém, se p-value > α, a probabilidade de se cometer erro tipo I é maior do que a aceitável, o que nos faz aceitar a Ho.
Referência bibliográfica: Triola F. Mario, Estatística
b) Resposta:
Ho: A média de idade das gestantes hipertensas é igual a média de idade das gestantes não hipertensas. (µ = 28,9)
Ha: A média de idade das gestantes hipertensas é diferente da média de idade das gestantes não hipertensas.
Nível de significância (α): α = 0,05 ( Aceitaremos Ho se -12,706< tCALC.< 12,706)
Estatística do teste: Usaremos o teste t, uma vez que não conhecemos o σ e a população é normalmente distribuída.

Vemos que o t calculado está fora da região crítica, o que favorece a Ho ( está na área branca do gráfico): Interpretação do valor de p e conclusão: p =0,07 significa que a probabilidade da diferença de idades ter sido ao acaso é de 7%. Observamos, então, que este valor é maior do que o nível de significância (α= 0,05). Dessa forma, aceitamos a Ho como verdadeira, ou seja, a média de idade das gestantes hipertensas é igual a média de idade das gestantes não hipertensas, o que nos mostra que a idade materna não tem relação com o desenvolvimento de hipertensão arterial.
Teste de hipóteses
· Primeiro passo: Formular a Hipótese nula (Ho) e a Hipótese alternativa (Ha)
Ho é uma afirmação que diz que o valor de uma parâmetro populacional (ex.: média e desvio padrão) é igual a um outro valor especificado (podem-se usar os símbolos ≤ ou ≥, mas, na maioria das vazes o = é o usado). Supõe-se que ela seja verdadeira e faz-se o teste para confirmá-la ou descartá-la. Já Ha é uma afirmativa que difere da Ho. Podem-se usar os símbolos >, < ou ≠.
· Segundo passo: Escolher o nível de significância
Nível de significância (α): é a probabilidade de a estatística teste cair na região crítica quando a Ho for verdadeira, ou seja, é a probabilidade de rejeitarmos a Ho quando ela é verdadeira (erro tipo I). Valores comuns são 0,05; 0,01 e 0,10.
Obs.: Nos testes bilaterais, o valor de α é dividido igualmente entre as duas caudas que correspondem à região crítica.

· Terceiro passo: Calcular a estatística do teste
Estatística de teste: é um valor encontrado que converte proporção, média ou desvio padrão em um score que permitirá a tomada de decisão acerca da Ho.
1) Para a proporção, usa-se:
2) Para média, usam-se: ou
3) Para o desvio padrão, usa-se:
= proporção amostral
= média amostral
= desvio padrão amostral
= desvio padrão populacional
= tamanho da amostra
obs.: Nos casos em que não se conhece o σ e a população é normalmente distribuída, ou quando σ é desconhecido e n > 30 usa-se a distribuição t, e não a z.
· Quarto passo: comparar o valor do teste com o da região crítica
Região crítica: são todos os valores que nos fazem rejeitar a Ho
Valor crítico: é qualquer valor que separa a região crítica dos valores que não levam a rejeição da Ho. Encontram-se os valores críticos nas tabelas de distribuição.
· Quinto passo: interpretar o valor-p do teste estatístico
Valor p: é a probabilidade calculada de se obter os dados observados se a Ho for verdadeira, ou seja, é a probabilidade de ter sido ao acaso.
· Sexto passo: Tomar uma decisão

Se o valor do teste exceder a região crítica, rejeitamos a Ho. Caso contrário, aceitamo-lo.
Referências bibliográficas: Triola F. Mario, Estatística; Velarde C. G. Luis, Noções de bioestatística; Informática Medica USP (http://fm.usp.br/dim/testez/index.php)
C) Resposta: Não
Justificativa: Como estamos estudando grupos independentes e queremos saber a associação entre duas variáveis categóricas (fator de interesse x doença), usaremos conceitos do teste Qui Quadrado(χ²), que nos mostra a distância matemática entre os valores esperados (ao acaso) e os reais (observados). Se essa distância é grande (χ² grande e p-value pequeno), concluímos que há forte associação entre preditor-desfecho e descartamos a Ho.

Para resolver a questão, foi usado o programa Epi Info™, que analisa dados estatísticos. Colocando os preditores na coluna (raça branca e não branca) e os desfechos (presença ou não de hipertensão) na linha, obeteremos os cálculos de valores como p-value e χ². Nos resultados, χ² (0,0826) é menor que p-value (0,39718459). Desse modo, como o valor de qui-quadrado é pequeno e o p é maior que o admitido (p<0,05), admitimos a hipótese nula de que não há associação entre este par de preditor-desfecho.
Teste Qui-quadrado
O teste qui-quadrado mostra a distância matemática entre os valores esperados (isto é, ao acaso) e os reais (observados numa pesquisa), avaliando, assim, a presença de associação entre as variáveis. Estas são geralmente categóricas, isto é, qualitativas (Ex: Fator de exposição X Doença). Além disso, os grupos devem ser independentes, os dados amostrais aleatórios e não há exigência de distribuição normal das variáveis. No teste Qui-quadrado de Pearson, para toda célula, a frequência esperada é de no mínimo 5, analisando N-fatores X N-desfechos. Já no de Fisher, que analisa 1 fator X 1 desfecho, a frequência esperada é menor que cinco.O cálculo é feito da seguinte forma:
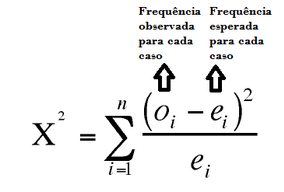
Para encontrar a frequência esperada para cada caso, fazemos uma tabela com os valores observados (preditor na coluna e desfecho na linha) e calculamos do seguinte modo:
| Doença sim | Doença não | |
|---|---|---|
| Fator presente | A | B |
| Fator ausente | C | D |
Probabilidade do acaso de A, por exemplo: Pa = ou seja (Linha x Coluna)Total

Assim, pode-se testar a hipótese nula (Ho) de que não há associação entre os fatores. Um qui-quadrado pequeno mostra que a ocorrência está próxima do esperado (nos leva a aceitar a hipótese nula como verdadeira). Já quando o valor é grande, há grande diferença entre o esperado e o observado, levando-nos a rejeitar a hipótese nula.
Referências bibliográficas: Triola F. Mario, Estatística; Velarde C. G. Luis, Noções de bioestatística; Biometria -Qui-quadrado-UFPA (http://www.ufpa.br/dicas/biome/bioqui.htm), CDC (https://www.cdc.gov/epiinfo/index.html).
Indexadores do tema deste exercício
[editar | editar código-fonte]Preparação e análise de tabelas sobre dados de saúde
Apresentação de dados científicos sobre saúde
Comparação entre grupos amostrais em saúde
Bibliografia utilizada
[editar | editar código-fonte]Triola F. Mario, Estatística
Velarde C. G. Luis, Noções de bioestatística
Biometria -Qui-quadrado-UFPA (http://www.ufpa.br/dicas/biome/bioqui.htm)
CDC (https://www.cdc.gov/epiinfo/index.html)
Informática Medica USP (http://fm.usp.br/dim/testez/index.php)













