Mecânica dos fluidos/Camada limite
Camada limite
[editar | editar código-fonte]Geral
[editar | editar código-fonte]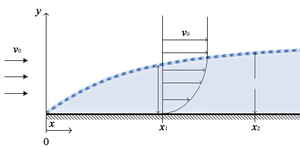
Para uma introdução à teoria da camada limite, examinemos o escoamento de ar em torno de uma asa de avião. O fenômeno só pode ser corretamente entendido se levarmos em conta a viscosidade do fluido. No século XVIII, d'Alembert demonstrou que, se desprezarmos a viscosidade do ar ao analisar o escoamento em torno de um objeto sólido, chegaremos à conclusão que esse objeto não estaria sujeito a nenhuma resistência do meio ao seu movimento, o que contradiz a experiência. No entanto, apenas no início do século XX foi oferecida uma explicação satisfatória do fenômeno, por Prandtl.
A explicação de Prandtl é que, embora o escoamento do fluido apresente número de Reynolds muito elevado, o que indica que o efeito da viscosidade é desprezível, na região próxima ao objeto ele é sempre laminar. Assim, em situações em que o efeito das interfaces do fluido com superfícies sólidas tiver que ser levado em conta, o modelo do líquido ideal não poderá ser utilizado.
Tudo isso está de acordo com o princípio da aderência completa, já visto anteriormente. O perfil de velocidades resultante parte de v = 0 junto à superfície (y = 0) até um valor constante a uma distância determinada y(x2) da mesma (dito de outro modo: a camada limite cresce de 0 em x = 0 até y(x2) em x = x2).
A figura abaixo ilustra com mais detalhes o fenômeno. O escoamento não é perturbado antes de o fluido entrar em contato com a asa (x < 0). A partir de x = 0, a asa começa a perturbar o escoamento; o princípio da aderência completa faz com que o perfil de velocidades assuma a forma de uma parábola; nas proximidades da superfície, a velocidade é pequena o bastante para que o escoamento seja laminar; é a chamada camada limite laminar. Fora da camada limite, o escoamento é, normalmente, turbulento. O ponto x = 0 é chamado de ponto de estagnação, porque ali a velocidade é nula.

A velocidade de uma partícula de fluido próxima à asa vai diminuindo, a partir de x = 0, devido à fricção. No ponto 4, a velocidade atinge o valor nulo; a partícula, nesse ponto, não mais acompanha o traçado da asa, e sim é afastada da sua posição por outras partículas que chegam a esse mesmo ponto depois dela. Por isso, o ponto 4 é chamado ponto de separação; nele, o fluido perde o contato com a superfície, e a camada limite laminar desaparece.
No entanto, depois do ponto de separação, continua havendo espaço ocupado pelo fluido. O fluido nesse local consiste de partículas que retornam a ter contato com a asa após serem expulsas pelas outras no ponto 4. Como mostra a figura, o fluxo está em movimento contrário ao original. Esse fluxo é chamado de fluxo secundário. A camada limite, nesse caso, é chamada camada limite separada.
A pressão na camada limite separada é sempre baixa. No ponto de estagnação, como é fácil de se ver, a pressão é grande. Essa diferença de pressão tende a frear o fluido. A perda de velocidade adicional causada por essa diferença de pressão é muito maior que a causada pela fricção. Esse efeito é chamado arrasto aerodinâmico da asa, e sua magnitude depende principalmente da forma da asa e sua posição com relação ao fluxo.
Assim, conclui-se que, realmente, para um fluido pouco viscoso a influência direta da fricção é pequena. No entanto, a influência indireta, que se manifesta no arrasto aerodinâmico, é sempre importante, especialmente no caso de objetos pouco aerodinâmicos, como o mostrado na figura abaixo. Um objeto é tão melhor, do ponto de vista aerodinâmico, quanto mais afastado do ponto de estagnação estiver o ponto de separação.

Para valores de x entre os pontos de estagnação e de separação, verifica-se que a espessura da camada limite laminar vai diminuindo progressivamente; comparem-se, na figura, as espessuras nos pontos 1 e 3. Entre a camada limite laminar e a região do fluido onde o escoamento é plenamente turbulento, aparecem regiões em que o escoamento não é mais puramente laminar: são as regiões de camada limite turbulenta (região 6 na figura) e de camada limite de transição (região 2 na figura). O escoamento na camada limite turbulenta, apesar de turbulento, tem características diferentes do escoamento na região externa à camada limite, como veremos mais à frente.

