Iniciação à Pesquisa Científica em Saúde /REPOSITÓRIO DE EXERCÍCIOS RESOLVIDOS/ Exercício 22: Inteligência

Questão 22: Inteligência I[editar | editar código-fonte]

Os autores de um estudo original testaram a suposição de que o QI foi influenciado pelo PIB do país, logo sem surpresa, que as posições mais elevadas entre países seriam determinadas também pela renda^[1]. Hong Kong não é propriamente um país, mas como uma região administrativa especial da China. A região é altamente classificada em matemática e ciência, e fica apenas atrás da Finlândia na lista da OECD para qualidade de educação. O QI médio em Hong Kong foi o maior do mundo, valor médio: 117 (para esta atividade, vamos supor um desvio padrão de 15 pontos). Responda:

a) Construa um histograma de frequência para valores de QI em Hong Kong, baseando-se nas propriedades da distribuição normal

b) Calcule o coeficiente de variação para ter uma idéia da variabilidade deste indicador

c) Acredita-se que Albert Einstein tinha um QI de 160. Qual a diferença entre o QI de Einstein e o da média da população de Hong Kong? Converta o QI de Einstein em escore Z

e) Se considerarmos o QI usual entre – 2 e +2 desvios-padrão da média, o QI de Einstein era usual?

Resposta da questão:[editar | editar código-fonte]

a) Baseando-se nas propriedades de distribuição normal e utilizando os dados fornecidos no enunciado da questão pode-se desenhar uma curva de Gauss como a que se segue:

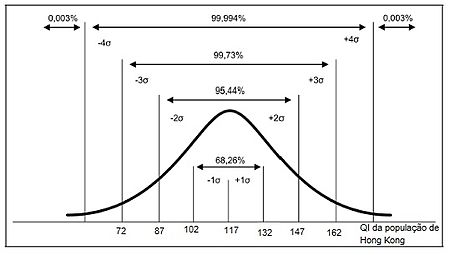
O acréscimo e o decréscimo de um desvio-padrão ao valor da média representa 68,26% da população analisada; de dois desvios-padrão corresponde a 95,44% da população e de três desvios-padrão correspondem à 99,73% do conjunto.

A equação da curva Normal é especificada usando 2 parâmetros: a média , e o desvio padrão .A média refere-se ao centro da distribuição e o desvio padrão ao espalhamento (ou achatamento) da curva.A distribuição normal é simétrica em torno da média o que implica que e média, a mediana e a moda são todas coincidentes.

Utilizando as porcentagens fornecidas pela distribuição gaussiana, pode-se construir um histograma de frequência (ao lado) tendo no eixo das abscissas os intervalos de QI e no eixo das ordenadas a porcentagem da população que tem valor de QI dentro de determinado intervalo. Vale ressaltar que o histograma é um gráfico composto por retângulos justapostos em que a base de cada um deles corresponde ao intervalo de classe e a sua altura à respectiva freqüência.

b) Entre as medidas de dispersão, o coeficiente de variação relaciona o desvio-padrão de um conjunto de dados à sua média. Trata-se de uma medida de variabilidade relativa.

Ele é expresso comparando-se o desvio-padrão representado por S , com a média, representado por ${\bar {x}}$ , através da razão entre essas medidas.

No exercício proposto, o Coeficiente de Variação (CV) é :

CV = S/ ${\bar {x}}$ , ou seja,

CV= 15/117

CV=0,128 ou 12,8%

Algumas vezes, o coeficiente de variação é ainda multiplicado por 100, passando a ser expressado como percentagem. O resultado é, então, utilizado para se analisar a dispersão em termos relativos. Quanto menor for o valor do coeficiente de variação, mais homogêneos serão os dados, ou seja, menor será a dispersão em torno da média. De uma forma geral, se o CV:

For menor ou igual a 15% → baixa dispersão: dados homogêneos

For entre 15 e 30% → média dispersão

For maior que 30% → alta dispersão: dados heterogêneos

Assim, o valor encontrado no exercício propõe que os dados são homogêneos, o que é esperado tendo em vista a distribuição normal.

c) A diferença entre o QI de Einstein e o da média da população de Hong Kong é

160 - 117 = 43

O Z-ESCORE PARA O QI DE EINSTEIN É 43 / 15 = 2,9 DESVIOS PADRÕES

Tendo o desvio padrão de 15, podemos classificar essa diferença entre 2 e 3 desvios padrões ( 2dp - 30; 3dp-45) tendo uma maior proximidade com os valores relativos a 3dp.

Essa análise, permite a conversão do QI de Eisntein em escore z, uma vez que é o quanto uma medida se afasta da média em termos de Desvios Padrão.

• Quando o escore Z é positivo isto indica que o dado está acima da média e quando o mesmo é negativo significa que o dado está abaixo da média.Seus valores oscilam entre -3 < Z < +3 e isto corresponde a 99,72% da área sob a curva da Distribuição Normal.

Portanto, o QI de Eistein se encontra entre escore +2< z< +3, estando mais próximo da curva de +3.

e) Uma vez que se considere um QI usual quando este estiver entre – 2 e +2 desvios-padrão da média, conclui-se que o QI de Einstein era não era usual, pois, conforme visto na questão anterior, seu QI estaria entre 2 e 3 desvios padrões (2dp - 30; 3dp-45) tendo uma maior proximidade com os valores relativos a 3dp.