Matemática elementar/Trigonometria/Arcos e ângulos
Circunferência[editar | editar código-fonte]
Seja um ponto qualquer do plano e um número real. A circunferência de centro e raio é o lugar geométrico dos pontos desse plano tais que
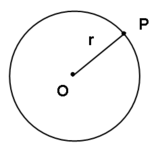
Veja no Wikicionário círculo.
Arco de circunferência[editar | editar código-fonte]
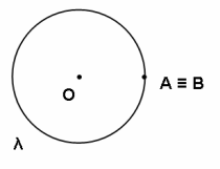
Consideremos uma circunferência de centro Sejam e dois pontos distintos de
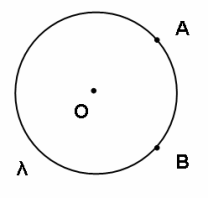
Um arco de circunferência de extremos e é cada uma das partes em que fica dividida uma circunferência por dois de seus pontos.
Quando teremos dois arcos: o arco nulo (um ponto) e o arco de uma volta (uma circunferência).
Arco de circunferência e ângulo central correspondente[editar | editar código-fonte]
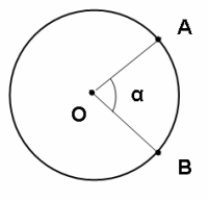
A medida de um arco é, por definição, a medida do ângulo central correspondente. Medir significa comparar com uma unidade padrão previamente adotada. Contudo, para evitar possíveis divergências na escolha da unidade para medir um mesmo arco, as unidades de medida restringem-se a três principais: o grau (), o radiano () e o grado, sendo este último não muito comum.
O grau[editar | editar código-fonte]

Um grau é um arco de circunferência cujo comprimento equivale a da circunferência que contém o arco a ser medido. Portanto, a medida, em graus, de um arco de uma volta completa (uma circunferência) é
- Submúltiplos do grau
- O minuto ou seja,
- O segundo ou seja, e
O radiano[editar | editar código-fonte]
Um radiano é um arco de circunferência cujo comprimento é igual ao raio da circunferência que contém o arco a ser medido. É a unidade do Sistema Internacional (SI).
Conseqüentemente, para medir um ângulo em radianos, convém calcular a razão entre o comprimento do arco pelo raio ou seja, calcular quantos radianos mede o arco Portanto, como consequência da definição de radiano, podemos estabelecer a seguinte relação:
onde e devem estar na mesma unidade de comprimento.
O comprimento de uma circunferência de raio é Logo, a medida do arco de uma volta completa, em radianos, é Para converter unidades, podemos usar as correspondências ou e uma regra de três simples.
O grado[editar | editar código-fonte]
Ver artigo na wikipedia Grado O grado foi introduzido junto com o Sistema métrico, durante a Revolução francesa mas, ao contrário do sucesso das outras medidas, não pegou. Atualmente, ele é apenas utilizado nos trabalhos topográficos e geodésicos feitos na França.
É a medida de um arco cujo comprimento equivale a da circunferência que contém o arco a ser medido. É evidente que, para conversão de unidades, pode-se utilizar as relações ou e uma regra de três simples.
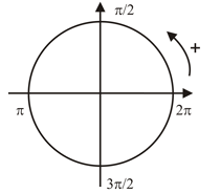
O ciclo trigonométrico[editar | editar código-fonte]
Consideremos no plano um sistema de eixos perpendiculares em que Seja uma circunferência de centro raio e o ponto

A cada número real associaremos um único ponto de
- Se então tomamos
- Se realizamos, a partir de um percurso de comprimento no sentido anti-horário e marcamos o ponto como final desse percurso.
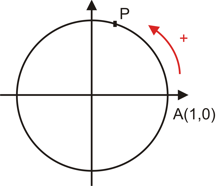
- Se realizamos, a partir de um percurso de comprimento no sentido horário, e marcamos o ponto como final desse percurso.

Assim, a circunferência sobre a qual foi fixado o ponto como orientação é chamada ciclo trigonométrico ou circunferência trigonométrica.
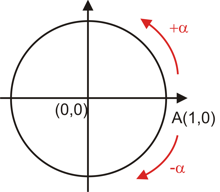
O ponto é chamado imagem de no ciclo trigonométrico.
O sistema de eixos perpendiculares divide o ciclo trigonométrico em quatro partes, cada uma das quais é chamada quadrante.

Ângulos côngruos[editar | editar código-fonte]
Os ângulos e em graus, são côngruos ou congruentes se, e somente se, para algum ou seja, se e têm a mesma imagem no ciclo trigonométrico. Para indicar que e são côngruos escrevemos
Por exemplo, os ângulos e são congruentes, pois
Expressão geral dos arcos que têm imagem em um ponto do ciclo trigonométrico..[editar | editar código-fonte]
Consideremos um sistema de eixos perpendiculares e uma circunferência de centro e raio Sendo um ponto qualquer pertencente à a imagem de um ângulo na circunferência, podemos estabelecer uma expressão geral dos arcos que têm imagem em um determinado ponto do ciclo trigonométrico.

Por exemplo, a expressão geral dos arcos que têm imagem no ponto dar-se-á por ou sendo o número de voltas completas. Quando deve-se andar no sentido anti-horário; se deve-se andar no sentido horário.
Analogamente, temos:
- Para ou
- Para ou
- Para ou
- Para ou ou
- Para ou ou
- Para ou ou ou ou

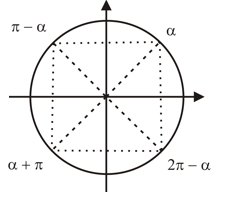
Considerando a figura acima, a expressão geral dos arcos que têm imagem em ou é:
- em graus:
- em radianos:
Expressão geral dos arcos que têm imagem em
- em graus:
- em radianos:
No caso da figura seguinte, a expressão geral dos arcos fica:
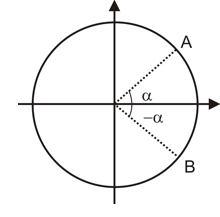
- em graus:
- em radianos:
Primeira determinação positiva[editar | editar código-fonte]
A primeira determinação positiva de um ângulo é o menor ângulo côngruo que seja positivo.
Por exemplo, os ângulos (em graus) -15o, 315o, 2115o, -2505o são congruentes, sendo sua primeira determinação positiva o ângulo 315o.
Analogamente, os ângulos (em radianos) , e são congruentes, sendo sua primeira determinação positiva o ângulo .
Para se resolver o problema de determinar a primeira determinação positiva é preciso:
- dividir o ângulo pelo valor do círculo trigonométrico (360o ou , conforme o problema seja apresentado em graus ou radianos)
- se este número não for inteiro, arredondar o valor para o valor inteiro imediatamente inferior
- tomar o número inteiro com sinal contrário (ou seja, se o passo anterior obteve n, obter agora -n)
- somar ao ângulo inicial este valor inteiro do passo acima multiplicado pelo círculo trigonométrico (360o ou , conforme o problema seja apresentado em graus ou radianos)
Exemplos:
- Se o ângulo inicial é -580o
- Dividir -580 por 360 -> -1,(alguma coisa) (note que não é preciso fazer a divisão até o fim, já que estamos apenas interessados na parte inteira da divisão)
- Não sendo inteiro, tomar a parte inteira -> -2
- Trocar o sinal -> 2
- Somar -580o com 2 x 360o -> 140o
- Se o ângulo inicial é
- Dividir por -> 4
- Sendo inteiro, manter -> 4
- Trocar o sinal -> -4
- Somar com -> 0
- Se o ângulo inicial é
- Dividir por -> ou, aproximadamente, 4,(alguma coisa)
- Não sendo inteiro, tomar a parte inteira -> 4
- Trocar o sinal -> -4
- Somar com ->
Imagens de alguns arcos importantes[editar | editar código-fonte]
- Primeira volta no sentido anti-horário:
Ângulos correspondentes[editar | editar código-fonte]
- Em graus:
- Em radianos: