Matemática elementar/Geometria plana/Triângulos

Tipos de triângulos

Classificação segundo a medida relativa dos lados

Um triângulo pode ser classificado de acordo com as medidas relativas de seus lados:

• Um triângulo equilátero possui todos os lados congruentes. Pode-se verificar que um triângulo eqüilátero é também eqüiângulo, ou seja, possui todos os seus ângulos internos congruentes (e com medida 60°). Por este motivo, este tipo de triângulo é também um polígono regular.
• Um triângulo isósceles possui pelo menos dois lados congruentes. Num triângulo isósceles, o ângulo formado pelos lados congruentes é chamado ângulo do vértice. Os demais ângulos denominam-se ângulos da base e, como se pode verificar, são congruentes. Note que os triângulos equiláteros também são isósceles.
• Em um triângulo escaleno, as medidas dos três lados são diferentes. É possível mostrar que os ângulos internos de um triângulo escaleno também possuem medidas diferentes.

Denomina-se base o lado sobre qual apóia-se o triângulo. No triângulo isósceles, considera-se base o lado de medida diferente.

A seguir é mostrada a classificação de alguns triângulos de acordo com o critério anterior:

Exemplo de triângulo equilátero

Este triângulo é equilátero, pois possui os três lados congruentes. Em particular, como seus lados são dois a dois congruentes, ele é um triângulo isósceles. Pode-se observar que seus todos os seus ângulos internos medem 60°, e por isso ele é equiângulo.

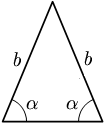
Exemplo de triângulo isósceles

Neste triângulo há somente dois lados congruentes: os que têm medida $b$. Por este motivo, o triângulo é isósceles, mas não é equilátero. Além disso, cada um destes dois lados forma um ângulo de medida $\alpha$ com a base do triângulo.

Exemplo de triângulo escaleno

Aqui, cada um dos lados tem um comprimento diferente dos demais. Assim, este é um triângulo escaleno. Observe ainda que nenhum par de ângulos internos tem a mesma medida.

Classificação de acordo com seus ângulos internos e externos em baixo

Um triângulo também pode ser classificado de acordo com seus ângulos internos:

• Um triângulo retângulo possui um ângulo reto. Num triângulo retângulo, denomina-se hipotenusa o lado oposto ao ângulo reto. Os demais lados chamam-se catetos. Os catetos de um triângulo retângulo são complementares.
• Um triângulo obtusângulo possui um ângulo obtuso e dois ângulos agudos.
• Em um triângulo acutângulo, todos os três ângulos são agudos.

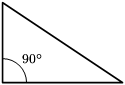
Exemplo de triângulo retângulo

• Um ângulo reto, ou seja, um ângulo de 90º.

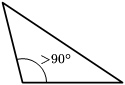
Exemplo de triângulo obtusângulo

• Um ângulo obtuso e dois ângulos agudos.

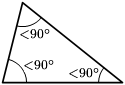
Exemplo de triângulo acutângulo

• Todos os três ângulos são agudos. Ou seja, menor que 90º

Soma dos ângulos internos

Na geometria euclidiana, de acordo com o teorema angular de Tales, a soma dos ângulos internos de qualquer triângulo é igual a dois ângulos retos (180° ou π radianos). Isso permite a determinação da medida do terceiro ângulo, desde que sejam conhecidas as medidas dos outros dois ângulos.

Soma dos ângulos externos

Existe também um corolário, que afirma que a medida de um ângulo externo de um triângulo é igual à soma das medidas dos ângulos internos não-adjacentes.

Exemplo: Se os ângulos internos de um triângulo forem: $60^{\circ },60^{\circ },60^{\circ }$ a resposta final será assim: Resolução: $x=60^{\circ }+60^{\circ }$, $x=120^{\circ }$. Porque o ângulo externo é a igual à soma dos ângulos internos duas vezes.

Relações de desigualdades entre lados e ângulos

1ª relação: Um ângulo externo de um triângulo é maior que qualquer um dos ângulos internos não-adjacentes.

2ª relação: Se dois lados de um triângulo tem medidas diferentes, ao maior lado opõe-se o maior ângulo e ao menor lado, opõe-se o menor ângulo.

3ª relação: Em todo triângulo, qualquer lado tem medida menor que a soma das medidas dos outros dois.

Área do triângulo

Existem várias formas de se expressar a área A de um triângulo:

• Dadas a base b e a altura h: $A={\frac {b\cdot h}{2}}$
• Dados dois lados a e b e o ângulo γ entre eles compreendido: $A={\frac {1}{2}}ab\sin {\gamma }$
• Dados os três lados a, b e c: $A={\sqrt {p(p-a)(p-b)(p-c)}}$, onde p é o semiperímetro (metade do perímetro). Essa fórmula é conhecida como fórmula de Heron.

Se o triângulo for equilátero de lado L, sua área pode ser obtida pela fórmula:

• $A={\frac {L^{2}{\sqrt {3}}}{4}}$

Congruência

Critério LLL

Lado-Lado-Lado.

Critério LAL

Lado-Ângulo-Lado.

Critério ALA

Ângulo-Lado-Ângulo.

Critério LLAr

Lado-Lado-Ângulo reto.

Semelhança

Critério LLL

Segundo o critério LLL (lado-lado-lado), existe semelhança entre dois triângulos se os três lados de um são proporcionais aos três lados correspondentes do outro.

Critério LAL

Segundo o critério LAL (lado-ângulo-lado), existe semelhança entre dois triângulos se têm entre si dois pares de lados correspondentes proporcionais e se os ângulos por eles formados forem iguais.

Critério AA

Segundo o critério AA (ângulo-ângulo), existe semelhança entre dois triângulos se eles têm dois ângulos iguais.

Referências

• Elementos de Geometria

Ver também

• Triângulo
• Triângulosh shsuw retângulo

Esta página é um esboço de geometria. Ampliando-a você ajudará a melhorar o Wikilivros.