Notas de Mecânica/Momentum de Inércia
Energia Cinética de Rotação
[editar | editar código-fonte]Analisaremos aqui a energia cinética de rotação de um corpo rígido.
Movimento circular de uma partícula única
[editar | editar código-fonte]Consideremos uma partícula de massa em um movimento circular de raio com velocidade de em torno de um eixo fixo. A partícula é mantida nesta trajetória circular por meio de uma haste fina e sem massa, a função desta haste é apenas manter a partícula nesta trajetória circular.

A energia cinética de rotação da partícula é simplesmente:
Lembremos agora a relação entre variaveis lineares e angulares no movimento de rotação, em particular o que relaciona a velocidade e a velocidade angular de uma partícula a saber:
Desta forma podemos reescrever a energia cinética como:
Movimento circular de um corpo rígido composto por duas partículas
[editar | editar código-fonte]Consideremos agora o movimento de rotação de duas partículas e respectivamente de massas e unidas por uma haste sem massa. O eixo fixo de rotação encontra-se a uma distância da partícula e a uma distância da partícula , como ilustrado na figura. Cada partícula terá sua trajetória circular particular e portanto a velocidade de cada partícula em módulo será diferente.

A energia cinética de rotação deste sistema é:
Contudo as partículas terão a mesma velocidade angular , e desta forma podemos usar: Logo podemos reescrever a energia cinética como:
Movimento circular de um corpo rígido composto por partículas
[editar | editar código-fonte]Consideramos agora a rotação de um corpo rigido em forma de uma placa fina (sem espessura) em torno de um eixo fixo no sentido antihorário, indicado na figura, que é perpendicular ao plano desta placa. Esta placa é composta de partículas cada uma localizada a do eixo e com massa .
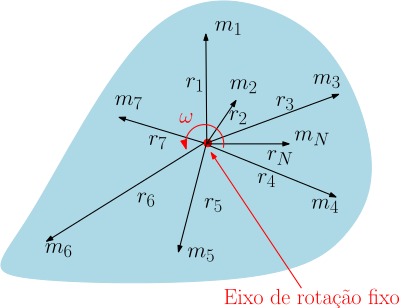
A energia cinética deste sistema de $N$ partículas é dada pela soma da energia cinética das partículas que o compoem:
Usamos agora que:
De maneira compacta:
Definição do momento de inércia
[editar | editar código-fonte]Acabamos de obter a energia cinética de um corpo que é composto de partículas, que reescrevemos como:
onde:
Se agora compararmos com a energia de translação deste corpo:
onde
Podemos interpretar
equação anterior como sendo uma medida da dificuldade de colocar um corpo
em movimento de rotação ou mudar este movimento, assim como
a massa do corpo é uma medida da dificuldade de colocar um corpo em movimento de translação ou mudar o movimento de translação do corpo.
Chamaremos então a quantidade de momentum de inércia do corpo ou inércia rotacional do corpo.
A unidade desta quantidade no SI é o
Propriedades do Momentum de inércia
[editar | editar código-fonte]O exemplo a seguir tem por intuito exemplificar uma das características do momentum de inércia:
Consideremos um corpo que é composto por duas partículas de massa e que estão conectadas por uma haste fina
e sem massa de comprimento .

a) Qual é o momentum de inércia do corpo considerando um eixo de rotação que passa pela partícula 1 e é perpendicular a haste?

b) Qual é o momentum de inércia do corpo considerando um eixo de rotação que passa pela partícula 2 e é perpendicular a haste?

Resumindo os dois casos :


Notamos que um mesmo corpo pode ter momenta de inércia diferentes dependendo do eixo em torno do qual estamos girando o corpo. No exemplo anterior a inércia rotacional é maior em torno do eixo que passa pela partícula 1 do que o eixo que passa pela partícula 2, ou seja:
O momentum de inércia é uma quantidade que depende do eixo que estamos girando o corpo.
Uma pergunta natural que podemos fazer agora é:
Em torno de que eixo a inércia rotacional possivel? Será o eixo que passa pela partícula 2 realmente a menor?
Para responder esta pergunta consideremos um caso genérico.

Cosideremos um eixo de rotação genérico distante da partícula 1 e perpendicular a haste.
a) Qual é o momentum de inércia em torno deste eixo genérico.
b) Para qual valor de teremos um mínimo de ?
Usaremos as condições de mínimo que você aprendeu nas suas aulas de cálculo:
Logo o calculado é realmente um mínimo
Notemos que este valor de é a posição do centro de massa colocando nossa origem sobre a partícula 1: Lembremos que a posição do CM de um sistema de partícula é dado por
Logo podemos concluir que o eixo que nos dá o menor momentum de inércia possível é aquele que passa pelo centro de massa do corpo.
E para nosso exemplo este momento de inércia mínimo é:

























































