Introdução à física/Espelhos esféricos

- Centro de curvatura (C): é o centro da esfera que deu origem ao espelho.
- Raio de curvatura (R): é o raio da esfera que deu origem ao espelho.
- Vértice (V): é o ponto mais externo da calota.
- Eixo principal: é a reta que passa pelo centro de curvatura e sai perpendicular ao vértice do espelho.
- Eixo secundário: qualquer reta que passe pelo centro de curvatura, menos a que é definida como eixo principal (passa pelo vértice). Existem infinitos eixos secundários na superfície do espelho.
- Ângulo de abertura (A): é o ângulo formado pelas extremidades da calota, delimitada por eixos secundários.
Os espelhos esféricos podem ser:
- Côncavos – a superfície refletora é a interna;
- Convexos – a superfície refletora é a externa.
Espelho esférico gaussiano
[editar | editar código-fonte]Espelhos esféricos gaussianos que obedecem as concondiçoes gerais de Gauss:
- O espelho deve apresentar uma abetura igual ou inferior a 10°.
- Os raios de luz devem ser paraxiais, ou seja, próximos do eixo principal e pouco inclinados em relação a ele.
Foco do espelho esférico
[editar | editar código-fonte]
Todo espelho esférico, ou circular, deve (regra geral) ter um foco. Esse foco é uma base para que a imagem possa ser formada. Toda imagem, seja num espelho côncavo ou convexo, tem suas retas traçadas com passagem pelo foco; ou seja se um objeto estiver precisamente "em cima" do foco a imagem não pode ser formada, nem pelo tracejamento de suas retas.
O foco f de um espelho esférico é dado por f = ; onde r é o raio do espelho; logo o raio do mesmo é o dobro do foco.
Para espelhos côncavos, f é um número positivo, mas para espelhos convexos, f é um número negativo.
Equação de Gauss
[editar | editar código-fonte]A relação acima descrita é um tanto simples, porém muito útil em determinadas questões; mesmo assim há uma outra equação que tem como resultado o foco de um espelho circular; é a Equação de Gauss que pode ser nomeada por: o inverso do foco é igual à soma dos inversos da distância da imagem e da distância do objeto. Assim:
- .
em que p, p' e f devem ser interpretados algebricamente, sendo números positivos quando estiverem do lado real do espelho e negativos quando estiverem do lado virtual do espelho.
p é sempre um número positivo. f é positivo em espelhos côncavos e negativo em espelhos convexos. p' é positivo em imagens reais e negativo em imagens virtuais.
Espelhos convexos
[editar | editar código-fonte] Neste caso, p é um número positivo, f é um número negativo, o que permite imediatamente concluir que é um número negativo (inverso da soma de dois números negativos) e de módulo menor que p. Portanto, a imagem e' sempre:
Neste caso, p é um número positivo, f é um número negativo, o que permite imediatamente concluir que é um número negativo (inverso da soma de dois números negativos) e de módulo menor que p. Portanto, a imagem e' sempre:
- Menor
- Direta
- Virtual
Espelhos côncavos
[editar | editar código-fonte]Neste caso, p e f são números positivos, portanto pode assumir qualquer valor diferente de zero.
Objeto colocado entre o infinito e o centro do espelho
[editar | editar código-fonte]- Menor
- Invertida
- Real
- Posicionada entre o centro (C) e o foco (F) do espelho
Objeto colocado no centro do espelho
[editar | editar código-fonte]- De mesmo tamanho
- Invertida
- Real
- Posicionada no centro (C) do espelho
Objeto colocado entre o centro e o foco do espelho
[editar | editar código-fonte]- Maior
- Invertida
- Real
- Posicionada entre o infinito e o centro do espelho
Objeto colocado sobre o foco do espelho
[editar | editar código-fonte]A imagem estará no infinito
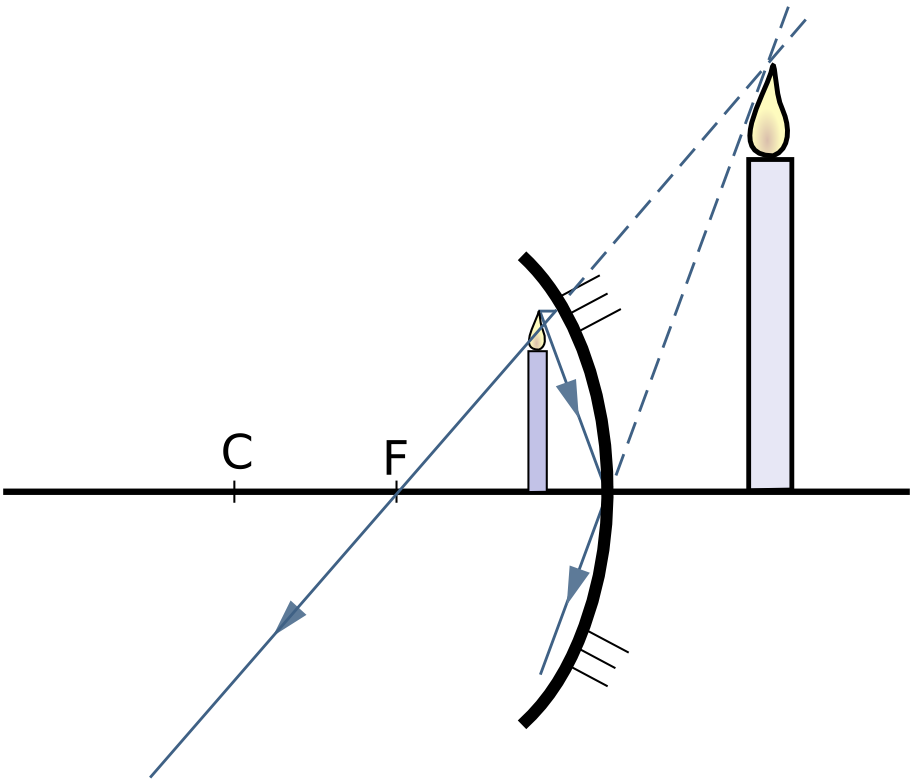
Objeto colocado entre o foco e o espelho
[editar | editar código-fonte]- Maior
- Direta
- Virtual
- Posicionada dentro do espelho
Ver também
[editar | editar código-fonte]
|
Esta página é um esboço de Física. Ampliando-a você ajudará a melhorar o Wikilivros. |