Geometria descritiva/Métodos descritivos/Mudança de plano
A Mudança de plano é uma ferramenta utilizada para trabalharmos com um objeto fixo no espaço de maneira conveniente na épura:
Mudando as projeções horizontais ou verticais (deste objeto) dos respectivos já conhecidos planos de projeção (π) ou (π') para outro plano convenientemente escolhido.
A seguir alguns exemplos de possíveis mudanças de plano.
Mudança de plano Vertical
[editar | editar código-fonte]Ponto
[editar | editar código-fonte]Construção Passo-a-Passo
[editar | editar código-fonte]- Desenhamos nossa nova épura de forma a representar o novo plano vertical desejado (Atente para os tracinhos, setas vermelhas).
- Traçamos uma linha de chamada para a nova épura passando pela projeção horizontal do ponto ( Aqui no desenho: A ).
- Transferimos a medida da Cota A' para a linha de chamada que acabamos de construir, achando assim A'1.
Reta
[editar | editar código-fonte]Construção Passo-a-Passo
[editar | editar código-fonte]Podemos formar uma reta apenas ligando dois pontos definidos no espaço, logo o processo é o mesmo utilizado anteriormente para os dois pontos da reta, que ligados formarão sua nova projeção Vertical.
Plano
[editar | editar código-fonte]Construção Passo-a-Passo
[editar | editar código-fonte]- Traçar r paralela a segunda linha de terra.
- Encontrar os traços (H) e (V)
- Encontrar r' ligando H' e V' por uma reta
- Calcular H'1 e V'1 encontrando assim r'1
- De acordo com uma das regras de pertinência de uma reta em um plano qualquer, o απ'1 deve ser paralelo a r'1 e encontrar com απ na segunda linha de terra.
Caso especial - Passo-a-Passo (Qualquer -> Vertical)
[editar | editar código-fonte]No caso de transformação de Plano Qualquer para Vertical podemos utilizar um algoritmo mais simples:
- Traçaremos nossa segunda linha de terra perpendicular a απ'
- Mude o ponto (W) do απ e encontre o ponto W1
- O απ1 se encontrará com απ' na segunda linha de terra e passará por W1
Mudança de plano Horizontal
[editar | editar código-fonte]Ponto
[editar | editar código-fonte]Construção Passo-a-Passo
[editar | editar código-fonte]- Desenhamos nossa nova épura de forma a representar o novo plano horizontal desejado (Atente para os tracinhos, setas vermelhas).
- Traçamos uma linha de chamada para a nova épura passando pela projeção vertical do ponto ( Aqui no desenho: A' ).
- Transferimos a medida do Afastamento de A para a linha de chamada que acabamos de construir, achando assim A1.
Reta
[editar | editar código-fonte]Construção Passo-a-Passo
[editar | editar código-fonte]Análogo ao Item 1.2.1: Fazemos a mudança de plano horizontal para dois pontos da reta e ligamos estes para formar a nova projeção Horizontal.
Plano
[editar | editar código-fonte]Construção Passo-a-Passo
[editar | editar código-fonte]Análogo ao item 1.3.1:
- Traçar r' paralela a segunda linha de terra.
- Encontrar os traços (H) e (V)
- Encontrar r ligando H e V por uma reta
- Calcular H1 e V1 encontrando assim r1
- De acordo com uma das regras de pertinência de uma reta em um plano qualquer, o απ1 deve ser paralelo a r1 e encontrar com απ' na segunda linha de terra.
Caso especial - Passo-a-Passo (Qualquer -> Topo)
[editar | editar código-fonte]Análogo ao item 2.3.2: No caso de transformação de Plano Qualquer para Topo podemos utilizar um algoritmo mais simples:
- Traçaremos nossa segunda linha de terra perpendicular a απ
- Mude o ponto (Q) do απ' e encontre o ponto Q'1
- O απ'1 se encontrará com απ na segunda linha de terra e passará por Q'1
Aplicações de Mudança de Plano
[editar | editar código-fonte]Reta
[editar | editar código-fonte]Achar a reta em Verdadeira Grandeza (V.G)
[editar | editar código-fonte]

Aplicações sucessivas
[editar | editar código-fonte]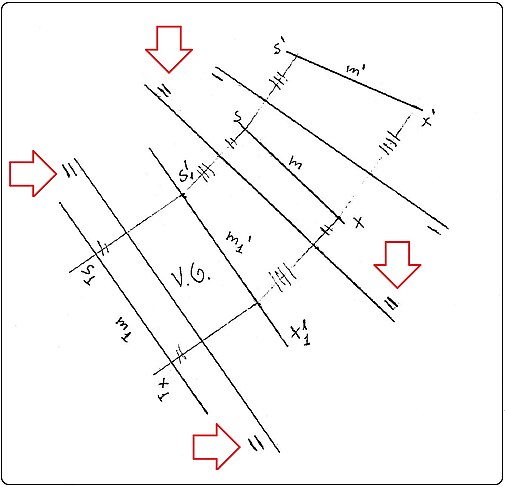

Plano
[editar | editar código-fonte]Achar a seção de Poliedros em V.G
[editar | editar código-fonte]









