Um produtor de cerveja dispõe de 240 kg de milho, 5 kg de lúpulo e 595 kg de malte. Para produzir um barril de cerveja preta se requer de 2,5 kg de milho, 0,125 kg de lúpulo e 17 kg de malte enquanto que, para produzir um barril de cerveja loira, se requer de 7,5 kg de milho, 0,125 kg de lúpulo e 10 kg de malte. Calcular a máxima produção para obter a maior receita sabendo que um barril de cerveja preta custa 180 reais enquanto que a loira custa 120 reais.
P
{\displaystyle P}
l
{\displaystyle l}
milho lúpulo malte
P
{\displaystyle P}
2
,
5
{\displaystyle 2{,}5}
0,125
{\displaystyle 0{,}125}
17
{\displaystyle 17}
l
{\displaystyle l}
7
,
5
{\displaystyle 7{,}5}
0,125
{\displaystyle 0{,}125}
10
{\displaystyle 10}
total
240
{\displaystyle 240}
5
{\displaystyle 5}
595
{\displaystyle 595}
max
f
(
P
,
l
)
=
180
P
+
120
l
{\displaystyle f(P,l)=180P+120l}
maximizar o lucro - esta é a função objetivo
s.a
2
,
5
P
+
7
,
5
l
≤
240
{\displaystyle 2{,}5P+7{,}5l\leq 240}
limite de quantidade de milho
0,125
P
+
0,125
l
≤
5
{\displaystyle 0{,}125P+0{,}125l\leq 5}
limite de quantidade de lúpulo
17
P
+
10
l
≤
595
{\displaystyle 17P+10l\leq 595}
limite de quantidade de malte
P
≥
0
→
−
P
≤
0
{\displaystyle P\geq 0\rightarrow -P\leq 0}
l
≥
0
→
−
l
≤
0
{\displaystyle l\geq 0\rightarrow -l\leq 0}
não se pode comprar uma quantidade negativa
Wikibooks , Wikipédia )
H
1
=
(
96
,
0
)
,
(
0
,
32
)
{\displaystyle H1=(96,0),(0,32)}
vetor normal
[
2
,
5
;
7
,
5
]
{\displaystyle [2{,}5;7{,}5]}
H
2
=
(
40
,
0
)
,
(
0
,
40
)
{\displaystyle H2=(40,0),(0,40)}
vetor normal
[
0,125
;
0,125
]
{\displaystyle [0{,}125;0{,}125]}
H
3
=
(
35
,
0
)
,
(
0
;
59
,
5
)
{\displaystyle H3=(35,0),(0;59{,}5)}
vetor normal
[
17
,
10
]
{\displaystyle [17,10]}
Para encontrar
P
=
96
{\displaystyle P=96}
l
=
32
{\displaystyle l=32}
H
1
{\displaystyle H1}
l
{\displaystyle l}
P
{\displaystyle P}
No Scilab , para visualizar o gráfico de
H
1
{\displaystyle H1}
x
=
[
96
;
0
]
{\displaystyle x=[96;0]}
y
=
[
0
;
32
]
{\displaystyle y=[0;32]}
plot
(
x
,
y
,
{\displaystyle {\text{plot}}(x,y,}
b
{\displaystyle b}
)
{\displaystyle )}
Wikibooks , Wikipédia ) tem quatro vértices e a solução é um deles. Então, calculando
P
{\displaystyle P}
l
{\displaystyle l}
f
(
P
,
l
)
{\displaystyle f(P,l)}
P
=
0
→
l
=
32
{\displaystyle P=0\rightarrow l=32}
Com as equações
2
,
5
P
+
7
,
5
l
≤
240
{\displaystyle 2{,}5P+7{,}5l\leq 240}
0,125
P
+
0,125
l
≤
5
→
P
=
12
{\displaystyle 0{,}125P+0{,}125l\leq 5\rightarrow P=12}
l
=
28
{\displaystyle l=28}
Com as equações
0,125
P
+
0,125
l
≤
5
{\displaystyle 0{,}125P+0{,}125l\leq 5}
17
P
+
10
l
≤
595
→
P
≈
27,857
14286
{\displaystyle 17P+10l\leq 595\rightarrow P\approx 27{,}85714286}
l
≈
12,142
85714
{\displaystyle l\approx 12{,}14285714}
l
=
0
→
P
=
35
{\displaystyle l=0\rightarrow P=35}
V
1
=
f
(
0
,
32
)
=
3.840
{\displaystyle V1=f(0,32)=3.840}
V
2
=
f
(
12
,
28
)
=
5.520
{\displaystyle V2=f(12,28)=5.520}
V
3
=
f
(
27
,
86
;
12
,
14
)
=
6.471
,
43
{\displaystyle {\color {Blue}V3=f(27{,}86;12{,}14)=6.471{,}43}}
V
4
=
f
(
35
,
0
)
=
6.300
{\displaystyle V4=f(35,0)=6.300}
Encontrando o segundo vértice pelo Scilab :
A
=
[
2.5
7.5
;
0.125
0.125
]
{\displaystyle A=[2.5\quad 7.5\quad ;\quad 0.125\quad 0.125]}
b
=
[
240
;
5
]
{\displaystyle b=[240\quad ;\quad 5]}
x
1
=
A
∖
b
{\displaystyle x1=A\setminus b}
A
x
=
b
{\displaystyle Ax=b}
x
1
=
[
12
28
]
{\displaystyle x1=[12\quad 28]}
O mesmo procedimento para outros vértices.
Lema de Farkas para verificar se, em cada vértice, não existe negatividade. Utilizando Scilab :
1º vértice:
A
=
[
2.5
7.5
;
−
1
0
]
{\displaystyle A=[2.5\quad 7.5\quad ;\quad -1\quad 0]}
B
=
A
′
{\displaystyle B=A'}
B
=
A
′
=
A
T
=
[
2.5
−
1
;
7.5
0
]
{\displaystyle B=A'=A^{T}=[2.5\quad -1\quad ;\quad 7.5\quad 0]}
c
=
[
180
;
120
]
{\displaystyle c=[180\quad ;\quad 120]}
u
=
B
∖
c
{\displaystyle u=B\setminus c}
[
16
−
140
]
{\displaystyle [16\quad -140]}
O mesmo procedimento para outros vértices:
No V2:
u
=
B
∖
c
{\displaystyle u=B\setminus c}
[
−
12
1680
]
{\displaystyle [-12\quad 1680]}
No V3:
u
=
B
∖
c
{\displaystyle u=B\setminus c}
[
274,285
71
8,571
4286
]
{\displaystyle {\color {Blue}[274{,}28571\quad 8{,}5714286]}}
No V4:
u
=
B
∖
c
{\displaystyle u=B\setminus c}
[
10,588
235
−
14,117
647
]
{\displaystyle [10{,}588235\quad -14{,}117647]}
Maximizar
u
(
x
,
y
)
=
7
x
1
/
2
y
1
/
3
{\displaystyle u(x,y)=7x^{1/2}y^{1/3}}
P
=
(
2
,
3
)
{\displaystyle P=(2,3)}
w
=
(
5
,
6
)
{\displaystyle w=(5,6)}
O
(
P
,
w
)
=
{
(
x
,
y
)
∈
R
2
:
⟨
(
2
,
3
)
,
(
x
,
y
)
⟩
≤
⟨
(
2
,
3
)
,
(
5
,
6
)
⟩
}
{\displaystyle O(P,w)=\{(x,y)\in \mathbb {R} ^{2}:\langle (2,3),(x,y)\rangle \leq \langle (2,3),(5,6)\rangle \}}
O
(
P
,
w
)
=
{
(
x
,
y
)
∈
R
2
:
2
x
+
3
y
≤
28
,
x
≥
0
,
y
≥
0
}
{\displaystyle O(P,w)=\{(x,y)\in \mathbb {R} ^{2}:2x+3y\leq 28,x\geq 0,y\geq 0\}}
O
{\displaystyle O}
P
{\displaystyle P}
w
{\displaystyle w}
max
7
x
1
/
2
y
1
/
3
{\displaystyle 7x^{1/2}y^{1/3}}
s.a
2
x
+
3
y
≤
28
{\displaystyle 2x+3y\leq 28}
−
x
≤
0
{\displaystyle -x\leq 0}
não é ativa
−
y
≤
0
{\displaystyle -y\leq 0}
idem
u
(
x
,
y
)
{\displaystyle u(x,y)}
Wikibooks , Wikipédia ):
A
=
[
2
3
−
1
0
0
−
1
]
{\displaystyle A={\begin{bmatrix}2&3\\-1&0\\0&-1\end{bmatrix}}}
Cobb-Douglas não está definido nos eixos. A solução não pode ser de Canto .
g
(
x
,
y
)
=
2
x
+
3
y
−
28
{\displaystyle g(x,y)=2x+3y-28}
∇
g
(
x
,
y
)
=
[
2
3
]
{\displaystyle \nabla g(x,y)={\begin{bmatrix}2\\3\end{bmatrix}}}
f
(
x
,
y
)
=
7
x
1
/
2
y
1
/
3
{\displaystyle f(x,y)=7x^{1/2}y^{1/3}}
∇
f
(
x
,
y
)
=
[
7
2
x
−
1
/
2
y
1
/
3
7
3
x
1
/
2
y
−
2
/
3
]
{\displaystyle \nabla f(x,y)={\begin{bmatrix}{7 \over 2}x^{-1/2}y^{1/3}\\{7 \over 3}x^{1/2}y^{-2/3}\end{bmatrix}}}
∇
f
(
x
,
y
)
=
v
∇
g
(
x
,
y
)
{\displaystyle \nabla f(x,y)=v\nabla g(x,y)}
[
7
2
x
−
1
/
2
y
1
/
3
7
3
x
1
/
2
y
−
2
/
3
]
=
v
[
2
3
]
{\displaystyle {\begin{bmatrix}{7 \over 2}x^{-1/2}y^{1/3}\\{7 \over 3}x^{1/2}y^{-2/3}\end{bmatrix}}=v{\begin{bmatrix}2\\3\end{bmatrix}}}
7
2
x
−
1
/
2
y
1
/
3
=
2
v
{\displaystyle {7 \over 2}x^{-1/2}y^{1/3}=2v}
7
3
x
1
/
2
y
−
2
/
3
=
3
v
{\displaystyle {7 \over 3}x^{1/2}y^{-2/3}=3v}
v
≠
0
{\displaystyle v\neq 0}
7
2
x
−
1
/
2
y
1
/
3
7
3
x
1
/
2
y
−
2
/
3
=
2
v
3
v
→
3
2
y
x
=
2
3
→
y
=
4
9
x
{\displaystyle {{7 \over 2}x^{-1/2}y^{1/3} \over {7 \over 3}x^{1/2}y^{-2/3}}={2v \over 3v}\rightarrow {3 \over 2}{y \over x}={2 \over 3}\rightarrow y={4 \over 9}x}
2
x
+
3
x
−
28
=
0
{\displaystyle 2x+3x-28=0}
→
2
x
+
3
(
4
9
x
)
=
28
→
x
(
2
+
4
3
)
=
28
→
x
∗
=
84
10
=
8
,
4
{\displaystyle \rightarrow 2x+3\left({4 \over 9}x\right)=28\rightarrow x\left(2+{4 \over 3}\right)=28\rightarrow {\color {blue}x^{*}={84 \over 10}=8{,}4}}
y
∗
=
4
9
⋅
8
,
4
=
33
,
6
9
{\displaystyle {\color {blue}y^{*}={4 \over 9}\cdot 8{,}4={33{,}6 \over 9}}}
Maximizar
k
x
α
y
β
(
max
f
(
x
,
y
)
=
max
k
⋅
f
(
x
,
y
)
, se
k
>
0
)
{\displaystyle kx^{\alpha }y^{\beta }({\text{max }}f(x,y)={\text{max }}k\cdot f(x,y){\text{, se }}k>0)}
(
x
,
y
)
∈
O
(
P
,
w
)
{\displaystyle (x,y)\in O(P,w)}
P
(
p
1
,
p
2
)
{\displaystyle P(p_{1},p_{2})}
w
(
w
1
,
w
2
)
{\displaystyle w(w_{1},w_{2})}
O
(
P
,
w
)
=
{
(
x
,
y
)
∈
R
2
:
⟨
(
p
1
,
p
2
)
,
(
x
,
y
)
⟩
≤
⟨
(
p
1
,
p
2
)
,
(
w
1
,
w
2
)
⟩
,
x
≥
0
,
y
≥
0
}
{\displaystyle O(P,w)=\{(x,y)\in \mathbb {R} ^{2}:\langle (p_{1},p_{2}),(x,y)\rangle \leq \langle (p_{1},p_{2}),(w_{1},w_{2})\rangle ,x\geq 0,y\geq 0\}}
O
(
P
,
w
)
=
{
(
x
,
y
)
∈
R
2
:
p
1
x
+
p
2
y
≤
p
1
w
1
+
p
2
w
2
,
x
≥
0
,
y
≥
0
}
{\displaystyle O(P,w)=\{(x,y)\in \mathbb {R} ^{2}:p_{1}x+p_{2}y\leq p_{1}w_{1}+p_{2}w_{2},x\geq 0,y\geq 0\}}
max
k
x
α
y
β
{\displaystyle kx^{\alpha }y^{\beta }}
função objetivo
s.a
p
1
x
+
p
2
y
≤
p
1
w
1
+
p
2
w
2
{\displaystyle p_{1}x+p_{2}y\leq p_{1}w_{1}+p_{2}w_{2}}
função restrição
−
x
≤
0
{\displaystyle -x\leq 0}
equivalente a
x
≥
0
{\displaystyle x\geq 0}
−
y
≤
0
{\displaystyle -y\leq 0}
idem
Cobb-Douglas não está definido nos eixos. A solução não pode ser de Canto .
g
(
x
,
y
)
=
p
1
x
+
p
2
y
−
p
1
w
1
−
p
2
w
2
→
∇
g
=
[
p
1
p
2
]
{\displaystyle g(x,y)=p_{1}x+p_{2}y-p_{1}w_{1}-p_{2}w_{2}\rightarrow \nabla g={\begin{bmatrix}p_{1}\\p_{2}\end{bmatrix}}}
f
(
x
,
y
)
=
k
x
α
y
β
→
∇
f
=
[
k
α
x
α
−
1
y
β
k
β
x
α
y
β
−
1
]
{\displaystyle f(x,y)=kx^{\alpha }y^{\beta }\rightarrow \nabla f={\begin{bmatrix}k\alpha x^{\alpha -1}y^{\beta }\\k\beta x^{\alpha }y^{\beta -1}\end{bmatrix}}}
∇
f
(
x
,
y
)
=
v
∇
g
(
x
,
y
)
{\displaystyle \nabla f(x,y)=v\nabla g(x,y)}
[
k
α
x
α
−
1
y
β
k
β
x
α
y
β
−
1
]
=
v
[
p
1
p
2
]
{\displaystyle {\begin{bmatrix}k\alpha x^{\alpha -1}y^{\beta }\\k\beta x^{\alpha }y^{\beta -1}\end{bmatrix}}=v{\begin{bmatrix}p_{1}\\p_{2}\end{bmatrix}}}
v
≠
0
{\displaystyle v\neq 0}
k
α
x
α
−
1
y
β
k
β
x
α
y
β
−
1
=
v
p
1
v
p
2
→
α
β
x
−
1
y
1
=
p
1
p
2
→
y
=
(
β
α
⋅
p
1
p
2
)
x
{\displaystyle {k\alpha x^{\alpha -1}y^{\beta } \over k\beta x^{\alpha }y^{\beta -1}}={vp_{1} \over vp_{2}}\rightarrow {\alpha \over \beta }x^{-1}y^{1}={p_{1} \over p_{2}}\rightarrow y=\left({\beta \over \alpha }\cdot {p_{1} \over p_{2}}\right)x}
y
{\displaystyle y}
p
1
x
+
p
2
(
β
α
⋅
p
1
p
2
)
x
−
p
1
w
1
−
p
2
w
2
=
0
→
p
1
x
(
1
+
β
α
)
=
p
1
w
1
+
p
2
w
2
→
x
∗
=
p
1
w
1
+
p
2
w
2
p
1
⋅
(
α
α
+
β
)
{\displaystyle p_{1}x+p_{2}\left({\beta \over \alpha }\cdot {p_{1} \over p_{2}}\right)x-p_{1}w_{1}-p_{2}w_{2}=0\rightarrow p_{1}x\left(1+{\beta \over \alpha }\right)=p_{1}w_{1}+p_{2}w_{2}\rightarrow {\color {blue}x^{*}={p_{1}w_{1}+p_{2}w_{2} \over p_{1}}\cdot \left({\alpha \over \alpha +\beta }\right)}}
y
∗
=
β
α
⋅
p
1
p
2
⋅
(
p
1
w
1
+
p
2
w
2
p
1
)
⋅
(
α
α
+
β
)
=
(
p
1
w
1
+
p
2
w
2
p
2
)
⋅
(
β
α
+
β
)
{\displaystyle {\color {blue}y^{*}}={\beta \over \alpha }\cdot {p_{1} \over p_{2}}\cdot \left({p_{1}w_{1}+p_{2}w_{2} \over p_{1}}\right)\cdot \left({\alpha \over \alpha +\beta }\right){\color {blue}=\left({p_{1}w_{1}+p_{2}w_{2} \over p_{2}}\right)\cdot \left({\beta \over \alpha +\beta }\right)}}
Maximizar
k
x
α
y
β
z
γ
{\displaystyle kx^{\alpha }y^{\beta }z^{\gamma }}
(
x
,
y
,
z
)
∈
O
(
P
,
w
)
{\displaystyle (x,y,z)\in O(P,w)}
P
(
p
1
,
p
2
,
p
3
)
{\displaystyle P(p_{1},p_{2},p_{3})}
w
(
w
1
,
w
2
,
w
3
)
{\displaystyle w(w_{1},w_{2},w_{3})}
O
(
P
,
w
)
=
{
(
x
,
y
,
z
)
∈
R
3
:
⟨
(
p
1
,
p
2
,
p
3
)
,
(
x
,
y
,
z
)
⟩
≤
⟨
(
p
1
,
p
2
,
p
3
)
,
(
w
1
,
w
2
,
w
3
)
⟩
,
x
≥
0
,
y
≥
0
,
z
≥
0
}
{\displaystyle O(P,w)=\{(x,y,z)\in \mathbb {R} ^{3}:\langle (p_{1},p_{2},p_{3}),(x,y,z)\rangle \leq \langle (p_{1},p_{2},p_{3}),(w_{1},w_{2},w_{3})\rangle ,x\geq 0,y\geq 0,z\geq 0\}}
O
(
P
,
w
)
=
{
(
x
,
y
,
z
)
∈
R
2
:
p
1
x
+
p
2
y
+
p
3
z
≤
p
1
w
1
+
p
2
w
2
+
p
3
w
3
,
x
≥
0
,
y
≥
0
,
z
≥
0
}
{\displaystyle O(P,w)=\{(x,y,z)\in \mathbb {R} ^{2}:p_{1}x+p_{2}y+p_{3}z\leq p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3},x\geq 0,y\geq 0,z\geq 0\}}
max
k
x
α
y
β
z
γ
{\displaystyle kx^{\alpha }y^{\beta }z^{\gamma }}
função objetivo
s.a
p
1
x
+
p
2
y
+
p
3
z
≤
p
1
w
1
+
p
2
w
2
+
p
3
w
3
{\displaystyle p_{1}x+p_{2}y+p_{3}z\leq p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3}}
função restrição
−
x
≤
0
{\displaystyle -x\leq 0}
equivalente a
x
≥
0
{\displaystyle x\geq 0}
−
y
≤
0
{\displaystyle -y\leq 0}
idem
−
z
≤
0
{\displaystyle -z\leq 0}
idem
g
(
x
,
y
,
z
)
=
p
1
x
+
p
2
y
+
p
3
z
−
p
1
w
1
−
p
2
w
2
−
p
3
w
3
→
∇
g
=
[
p
1
p
2
p
3
]
{\displaystyle g(x,y,z)=p_{1}x+p_{2}y+p_{3}z-p_{1}w_{1}-p_{2}w_{2}-p_{3}w_{3}\rightarrow \nabla g={\begin{bmatrix}p_{1}\\p_{2}\\p_{3}\end{bmatrix}}}
f
(
x
,
y
,
z
)
=
k
x
α
y
β
z
γ
→
∇
f
=
[
k
α
x
α
−
1
y
β
z
γ
k
β
x
α
y
β
−
1
z
γ
k
γ
x
α
y
β
z
γ
−
1
]
{\displaystyle f(x,y,z)=kx^{\alpha }y^{\beta }z^{\gamma }\rightarrow \nabla f={\begin{bmatrix}k\alpha x^{\alpha -1}y^{\beta }z^{\gamma }\\k\beta x^{\alpha }y^{\beta -1}z^{\gamma }\\k\gamma x^{\alpha }y^{\beta }z^{\gamma -1}\end{bmatrix}}}
∇
f
=
v
∇
g
→
[
k
α
x
α
−
1
y
β
z
γ
k
β
x
α
y
β
−
1
z
γ
k
γ
x
α
y
β
z
γ
−
1
]
=
v
[
p
1
p
2
p
3
]
{\displaystyle \nabla f=v\nabla g\rightarrow {\begin{bmatrix}k\alpha x^{\alpha -1}y^{\beta }z^{\gamma }\\k\beta x^{\alpha }y^{\beta -1}z^{\gamma }\\k\gamma x^{\alpha }y^{\beta }z^{\gamma -1}\end{bmatrix}}=v{\begin{bmatrix}p_{1}\\p_{2}\\p_{3}\end{bmatrix}}}
v
≠
0
{\displaystyle v\neq 0}
k
α
x
α
−
1
y
β
z
γ
=
v
p
1
{\displaystyle k\alpha x^{\alpha -1}y^{\beta }z^{\gamma }=vp_{1}}
k
β
x
α
y
β
−
1
z
γ
=
v
p
2
{\displaystyle k\beta x^{\alpha }y^{\beta -1}z^{\gamma }=vp_{2}}
k
γ
x
α
y
β
z
γ
−
1
=
v
p
3
{\displaystyle k\gamma x^{\alpha }y^{\beta }z^{\gamma -1}=vp_{3}}
k
α
x
α
−
1
y
β
z
γ
p
1
=
k
β
x
α
y
β
−
1
z
γ
p
2
→
α
p
1
y
=
β
p
2
x
→
y
=
(
β
α
⋅
p
1
p
2
)
x
{\displaystyle {k\alpha x^{\alpha -1}y^{\beta }z^{\gamma } \over p_{1}}={k\beta x^{\alpha }y^{\beta -1}z^{\gamma } \over p_{2}}\rightarrow {\alpha \over p_{1}}y={\beta \over p_{2}}x\rightarrow y=\left({\beta \over \alpha }\cdot {p_{1} \over p_{2}}\right)x}
k
α
x
α
−
1
y
β
z
γ
p
1
=
k
γ
x
α
y
β
z
γ
−
1
p
3
→
α
p
1
z
=
γ
p
3
x
→
z
=
(
γ
α
⋅
p
1
p
3
)
x
{\displaystyle {k\alpha x^{\alpha -1}y^{\beta }z^{\gamma } \over p_{1}}={k\gamma x^{\alpha }y^{\beta }z^{\gamma -1} \over p_{3}}\rightarrow {\alpha \over p_{1}}z={\gamma \over p_{3}}x\rightarrow z=\left({\gamma \over \alpha }\cdot {p_{1} \over p_{3}}\right)x}
y
{\displaystyle y}
z
{\displaystyle z}
p
1
x
+
p
2
y
+
p
3
z
−
p
1
w
1
−
p
2
w
2
−
p
3
w
3
=
0
→
p
1
x
+
p
2
(
β
α
⋅
p
1
p
2
)
x
+
p
3
(
γ
α
⋅
p
1
p
3
)
x
=
p
1
w
1
+
p
2
w
2
+
p
3
w
3
{\displaystyle p_{1}x+p_{2}y+p_{3}z-p_{1}w_{1}-p_{2}w_{2}-p_{3}w_{3}=0\rightarrow p_{1}x+p_{2}\left({\beta \over \alpha }\cdot {p_{1} \over p_{2}}\right)x+p_{3}\left({\gamma \over \alpha }\cdot {p_{1} \over p_{3}}\right)x=p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3}}
p
1
x
+
β
α
p
1
x
+
γ
α
p
1
x
=
p
1
w
1
+
p
2
w
2
+
p
3
w
3
→
x
(
1
+
β
α
+
γ
α
)
=
p
1
w
1
+
p
2
w
2
+
p
3
w
3
p
1
{\displaystyle p_{1}x+{\beta \over \alpha }p_{1}x+{\gamma \over \alpha }p_{1}x=p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3}\rightarrow x\left(1+{\beta \over \alpha }+{\gamma \over \alpha }\right)={p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3} \over p_{1}}}
x
∗
=
(
α
α
+
β
+
γ
)
⋅
(
p
1
w
1
+
p
2
w
2
+
p
3
w
3
p
1
)
{\displaystyle {\color {blue}x^{*}=\left({\alpha \over {\alpha +\beta +\gamma }}\right)\cdot \left({p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3} \over p_{1}}\right)}}
y
∗
=
(
β
α
+
β
+
γ
)
⋅
(
p
1
w
1
+
p
2
w
2
+
p
3
w
3
p
2
)
{\displaystyle {\color {blue}y^{*}=\left({\beta \over {\alpha +\beta +\gamma }}\right)\cdot \left({p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3} \over p_{2}}\right)}}
z
∗
=
(
γ
α
+
β
+
γ
)
⋅
(
p
1
w
1
+
p
2
w
2
+
p
3
w
3
p
3
)
{\displaystyle {\color {blue}z^{*}=\left({\gamma \over {\alpha +\beta +\gamma }}\right)\cdot \left({p_{1}w_{1}+p_{2}w_{2}+p_{3}w_{3} \over p_{3}}\right)}}
Considere o problema de variações seguinte:
maximizar
J
(
x
)
=
∫
0
T
L
(
t
,
x
(
t
)
,
x
′
(
t
)
)
d
t
{\displaystyle J(x)=\int _{0}^{T}L(t,x(t),x'(t))dt}
x
(
0
)
=
x
0
{\displaystyle x(0)=x_{0}}
x
(
T
)
=
x
T
{\displaystyle x(T)=x_{T}}
equação de Euler e ache os extremais, quando:
P1:
J
(
x
)
=
∫
0
1
(
4
x
(
t
)
−
(
x
′
(
t
)
)
2
−
(
x
(
t
)
)
2
)
d
t
.
{\displaystyle {\text{P1: }}J(x)=\int _{0}^{1}(4x(t)-(x'(t))^{2}-(x(t))^{2})dt.}
L
(
t
,
x
(
t
)
,
x
′
(
t
)
)
=
4
x
(
t
)
−
(
x
′
(
t
)
)
2
−
(
x
(
t
)
)
2
{\displaystyle L(t,x(t),x'(t))=4x(t)-(x'(t))^{2}-(x(t))^{2}}
∂
L
∂
x
(
t
)
(
t
,
x
(
t
)
,
x
′
(
t
)
)
=
4
−
2
x
(
t
)
{\displaystyle {\partial L \over \partial x(t)}(t,x(t),x'(t))=4-2x(t)}
∂
L
∂
x
′
(
t
)
(
t
,
x
(
t
)
,
x
′
(
t
)
)
=
−
2
x
′
(
t
)
{\displaystyle {\partial L \over \partial x'(t)}(t,x(t),x'(t))=-2x'(t)}
d
d
t
[
∂
L
∂
x
′
(
t
)
(
t
,
x
(
t
)
,
x
′
(
t
)
)
]
=
−
2
x
″
(
t
)
{\displaystyle {d \over dt}\left[{\partial L \over \partial x'(t)}(t,x(t),x'(t))\right]=-2x''(t)}
Equação de Euler
∂
L
∂
x
(
t
)
(
t
,
x
(
t
)
,
x
′
(
t
)
)
−
d
d
t
[
∂
L
∂
x
′
(
t
)
(
t
,
x
(
t
)
,
x
′
(
t
)
)
]
=
0
{\displaystyle {\partial L \over \partial x(t)}(t,x(t),x'(t))-{d \over dt}\left[{\partial L \over \partial x'(t)}(t,x(t),x'(t))\right]=0}
4
−
2
x
(
t
)
−
(
−
2
x
″
(
t
)
)
=
0
→
2
x
″
(
t
)
−
2
x
(
t
)
+
4
=
0
→
x
″
(
t
)
−
x
(
t
)
+
2
=
0
{\displaystyle 4-2x(t)-(-2x''(t))=0\rightarrow 2x''(t)-2x(t)+4=0\rightarrow \color {blue}x''(t)-x(t)+2=0}
Equação Diferencial Ordinária (Wikibooks , Wikipédia )
x
(
t
)
=
x
p
(
t
)
+
x
h
(
t
)
{\displaystyle x(t)=x_{p}(t)+x_{h}(t)}
x
p
(
t
)
{\displaystyle x_{p}(t)}
equação de Euler ) e
x
h
(
t
)
{\displaystyle x_{h}(t)}
equação de Euler ).
x
″
(
t
)
−
x
(
t
)
+
2
=
0
→
x
p
(
t
)
=
2
{\displaystyle {\cancel {x''(t)}}-x(t)+2=0\rightarrow x_{p}(t)=2}
x
″
(
t
)
−
x
(
t
)
+
2
=
0
→
x
″
(
t
)
−
x
(
t
)
=
0
→
x
h
(
t
)
=
x
h
″
(
t
)
{\displaystyle x''(t)-x(t)+{\cancel {2}}=0\rightarrow x''(t)-x(t)=0\rightarrow x_{h}(t)=x_{h}''(t)}
Na solução homogênea, substituir
x
n
{\displaystyle x^{n}}
λ
m
{\displaystyle \lambda ^{m}}
n
{\displaystyle n}
m
{\displaystyle m}
x
″
(
t
)
−
x
(
t
)
=
0
→
λ
2
−
λ
0
=
0
→
λ
=
±
1
{\displaystyle x''(t)-x(t)=0\rightarrow \lambda ^{2}-\lambda ^{0}=0\rightarrow \lambda =\pm 1}
Solução geral:
x
(
t
)
=
k
e
λ
t
+
2
=
k
1
e
t
+
k
2
e
−
t
+
2
{\displaystyle {\color {blue}x(t)}=ke^{\lambda t}+2={\color {blue}k_{1}e^{t}+k_{2}e^{-t}+2}}
Concavidade
∂
2
L
∂
x
(
t
)
2
=
−
2
{\displaystyle {\partial ^{2}L \over \partial x(t)^{2}}=-2}
∂
2
L
∂
x
(
t
)
∂
x
′
(
t
)
=
0
{\displaystyle {\partial ^{2}L \over \partial x(t)\partial x'(t)}=0}
∂
2
L
∂
x
′
(
t
)
∂
x
(
t
)
=
0
{\displaystyle {\partial ^{2}L \over \partial x'(t)\partial x(t)}=0}
∂
2
L
∂
x
′
(
t
)
2
=
−
2
{\displaystyle {\partial ^{2}L \over \partial x'(t)^{2}}=-2}
−
H
L
(
x
,
x
′
)
=
[
2
0
0
2
]
{\displaystyle -HL(x,x')={\begin{bmatrix}2&0\\0&2\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
(
t
)
{\displaystyle (t)}
i.e. , subentendendo-se
x
=
x
(
t
)
{\displaystyle x=x(t)}
x
′
=
x
′
(
t
)
{\displaystyle x'=x'(t)}
P2:
J
(
x
)
=
∫
0
1
(
1
+
(
x
′
(
t
)
)
2
)
1
2
d
t
.
{\displaystyle {\text{P2: }}J(x)=\int _{0}^{1}(1+(x'(t))^{2})^{1 \over 2}dt.}
L
(
t
,
x
(
t
)
,
x
′
(
t
)
)
=
(
1
+
(
x
′
(
t
)
)
2
)
1
2
→
L
(
t
,
x
,
x
′
)
=
(
1
+
(
x
′
)
2
)
1
2
{\displaystyle L(t,x(t),x'(t))=(1+(x'(t))^{2})^{1 \over 2}\rightarrow L(t,x,x')=(1+(x')^{2})^{1 \over 2}}
∂
L
∂
x
(
t
,
x
,
x
′
)
=
0
{\displaystyle {\partial L \over \partial x}(t,x,x')=0}
∂
L
∂
x
′
(
t
,
x
,
x
′
)
=
1
2
⋅
(
1
+
(
x
′
)
2
)
−
1
2
⋅
(
1
+
(
x
′
)
2
)
′
=
x
′
(
1
+
(
x
′
)
2
)
1
2
(
equivalente a
x
′
⋅
(
1
+
(
x
′
)
2
)
−
1
2
)
{\displaystyle {\partial L \over \partial x'}(t,x,x')={1 \over 2}\cdot (1+(x')^{2})^{-{1 \over 2}}\cdot \left(1+(x')^{2}\right)'={x' \over (1+(x')^{2})^{1 \over 2}}\left({\text{equivalente a }}x'\cdot (1+(x')^{2})^{-{1 \over 2}}\right)}
d
d
t
[
∂
L
∂
x
′
(
t
,
x
,
x
′
)
]
=
x
″
⋅
(
1
+
(
x
′
)
2
)
−
1
2
−
1
2
⋅
x
′
⋅
(
1
+
(
x
′
)
2
)
−
3
2
⋅
(
0
+
2
⋅
x
′
⋅
x
″
)
=
0
{\displaystyle {d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=x''\cdot (1+(x')^{2})^{-{1 \over 2}}-{1 \over 2}\cdot x'\cdot (1+(x')^{2})^{-{3 \over 2}}\cdot (0+2\cdot x'\cdot x'')=0}
Equação de Euler (substituir
(
1
+
(
x
′
)
2
)
{\displaystyle (1+(x')^{2})}
α
{\displaystyle \alpha }
∂
L
∂
x
(
t
,
x
,
x
′
)
−
d
d
t
[
∂
L
∂
x
′
(
t
,
x
,
x
′
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,x')-{d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=0}
−
x
″
α
1
2
+
(
x
′
)
2
⋅
x
″
α
3
2
=
−
α
⋅
x
″
+
(
x
′
)
2
⋅
x
″
α
3
2
=
0
→
−
x
″
−
(
x
′
)
2
⋅
x
″
+
(
x
′
)
2
⋅
x
″
=
0
→
x
″
(
t
)
=
0
{\displaystyle -{x'' \over \alpha ^{1 \over 2}}+{(x')^{2}\cdot x'' \over \alpha ^{3 \over 2}}={-\alpha \cdot x''+(x')^{2}\cdot x'' \over {\cancel {\alpha ^{3 \over 2}}}}=0\rightarrow -x''{\cancel {-(x')^{2}\cdot x''}}{\cancel {+(x')^{2}\cdot x''}}=0\rightarrow \color {blue}x''(t)=0}
Integrando
x
″
(
t
)
{\displaystyle x''(t)}
x
′
(
t
)
{\displaystyle x'(t)}
x
′
(
t
)
=
k
1
{\displaystyle x'(t)=k_{1}}
x
(
t
)
=
k
1
t
+
k
2
{\displaystyle \color {blue}x(t)=k_{1}t+k_{2}}
Concavidade
∂
2
L
∂
x
2
=
∂
2
L
∂
x
∂
x
′
=
∂
2
L
∂
x
′
∂
x
=
0
{\displaystyle {\partial ^{2}L \over \partial x^{2}}={\partial ^{2}L \over \partial x\partial x'}={\partial ^{2}L \over \partial x'\partial x}=0}
−
H
L
(
x
,
x
′
)
=
[
0
0
0
∂
2
L
∂
(
x
′
)
2
]
{\displaystyle -HL(x,x')={\begin{bmatrix}0&0\\0&{\partial ^{2}L \over \partial (x')^{2}}\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
P3:
J
(
x
)
=
∫
0
2
(
t
2
+
(
x
′
(
t
)
)
2
+
(
x
(
t
)
)
2
)
d
t
.
{\displaystyle {\text{P3: }}J(x)=\int _{0}^{2}(t^{2}+(x'(t))^{2}+(x(t))^{2})dt.}
L
(
t
,
x
(
t
)
,
x
′
(
t
)
)
=
t
2
+
(
x
′
(
t
)
)
2
+
(
x
(
t
)
)
2
→
L
(
t
,
x
,
x
′
)
=
t
2
+
(
x
′
)
2
+
x
2
{\displaystyle L(t,x(t),x'(t))=t^{2}+(x'(t))^{2}+(x(t))^{2}\rightarrow L(t,x,x')=t^{2}+(x')^{2}+x^{2}}
∂
L
∂
x
(
t
,
x
,
x
′
)
=
2
x
{\displaystyle {\partial L \over \partial x}(t,x,x')=2x}
∂
L
∂
x
′
(
t
,
x
,
x
′
)
=
2
x
′
{\displaystyle {\partial L \over \partial x'}(t,x,x')=2x'}
d
d
t
[
∂
L
∂
x
′
(
t
,
x
,
x
′
)
]
=
2
x
″
{\displaystyle {d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=2x''}
Equação de Euler
∂
L
∂
x
(
t
,
x
,
x
′
)
−
d
d
t
[
∂
L
∂
x
′
(
t
,
x
,
x
′
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,x')-{d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=0}
2
x
−
(
2
x
″
)
=
0
→
−
x
″
+
x
=
0
→
x
″
(
t
)
−
x
(
t
)
=
0
{\displaystyle 2x-(2x'')=0\rightarrow -x''+x=0\rightarrow \color {blue}x''(t)-x(t)=0}
Equação Diferencial Ordinária (Wikibooks , Wikipédia )
x
(
t
)
=
x
p
(
t
)
+
x
h
(
t
)
{\displaystyle x(t)=x_{p}(t)+x_{h}(t)}
x
p
(
t
)
{\displaystyle x_{p}(t)}
equação de Euler ) e
x
h
(
t
)
{\displaystyle x_{h}(t)}
equação de Euler ).
x
″
(
t
)
−
x
(
t
)
=
0
→
x
p
(
t
)
=
0
{\displaystyle {\cancel {x''(t)}}-x(t)=0\rightarrow x_{p}(t)=0}
x
″
(
t
)
−
x
(
t
)
=
0
→
x
h
(
t
)
=
x
h
″
(
t
)
{\displaystyle x''(t)-x(t)=0\rightarrow x_{h}(t)=x_{h}''(t)}
Na solução homogênea, substituir
x
n
{\displaystyle x^{n}}
λ
m
{\displaystyle \lambda ^{m}}
n
{\displaystyle n}
m
{\displaystyle m}
x
″
(
t
)
−
x
(
t
)
=
0
→
λ
2
−
λ
0
=
0
→
λ
=
±
1
{\displaystyle x''(t)-x(t)=0\rightarrow \lambda ^{2}-\lambda ^{0}=0\rightarrow \lambda =\pm 1}
Solução geral:
x
(
t
)
=
k
e
λ
t
=
k
1
e
t
+
k
2
e
−
t
{\displaystyle {\color {blue}x(t)}=ke^{\lambda t}={\color {blue}k_{1}e^{t}+k_{2}e^{-t}}}
Concavidade
∂
2
L
∂
x
2
=
2
{\displaystyle {\partial ^{2}L \over \partial x^{2}}=2}
∂
2
L
∂
x
∂
x
′
=
∂
2
L
∂
x
′
∂
x
=
0
{\displaystyle {\partial ^{2}L \over \partial x\partial x'}={\partial ^{2}L \over \partial x'\partial x}=0}
∂
2
L
∂
x
′
2
=
2
{\displaystyle {\partial ^{2}L \over \partial x'^{2}}=2}
−
H
L
(
x
,
x
′
)
=
[
−
2
0
0
−
2
]
{\displaystyle -HL(x,x')={\begin{bmatrix}-2&0\\0&-2\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
P4:
J
(
x
)
=
∫
0
5
(
t
x
′
(
t
)
+
(
x
′
(
t
)
)
2
)
d
t
.
{\displaystyle {\text{P4: }}J(x)=\int _{0}^{5}(tx'(t)+(x'(t))^{2})dt.}
L
(
t
,
x
(
t
)
,
x
′
(
t
)
)
=
t
x
′
(
t
)
+
(
x
′
(
t
)
)
2
→
L
(
t
,
x
,
x
′
)
=
t
x
′
+
(
x
′
)
2
{\displaystyle L(t,x(t),x'(t))=tx'(t)+(x'(t))^{2}\rightarrow L(t,x,x')=tx'+(x')^{2}}
∂
L
∂
x
(
t
,
x
,
x
′
)
=
0
{\displaystyle {\partial L \over \partial x}(t,x,x')=0}
∂
L
∂
x
′
(
t
,
x
,
x
′
)
=
t
+
2
x
′
{\displaystyle {\partial L \over \partial x'}(t,x,x')=t+2x'}
d
d
t
[
∂
L
∂
x
′
(
t
,
x
,
x
′
)
]
=
1
+
2
x
″
{\displaystyle {d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=1+2x''}
Equação de Euler
∂
L
∂
x
(
t
,
x
,
x
′
)
−
d
d
t
[
∂
L
∂
x
′
(
t
,
x
,
x
′
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,x')-{d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=0}
0
−
(
1
+
2
x
″
)
=
0
→
−
2
x
″
−
1
=
0
→
x
″
(
t
)
=
−
1
2
{\displaystyle 0-(1+2x'')=0\rightarrow -2x''-1=0\rightarrow \color {blue}x''(t)=-{1 \over 2}}
Integrando
x
″
(
t
)
{\displaystyle x''(t)}
x
′
(
t
)
{\displaystyle x'(t)}
k
{\displaystyle k}
x
′
(
t
)
=
−
1
2
t
+
k
1
{\displaystyle x'(t)=-{1 \over 2}t+k_{1}}
x
(
t
)
=
−
1
4
t
2
+
k
1
t
+
k
2
{\displaystyle x(t)=-{1 \over 4}t^{2}+k_{1}t+k_{2}}
Concavidade
∂
2
L
∂
x
2
=
∂
2
L
∂
x
∂
x
′
=
∂
2
L
∂
x
′
∂
x
=
0
{\displaystyle {\partial ^{2}L \over \partial x^{2}}={\partial ^{2}L \over \partial x\partial x'}={\partial ^{2}L \over \partial x'\partial x}=0}
∂
2
L
∂
(
x
′
)
2
=
2
{\displaystyle {\partial ^{2}L \over \partial (x')^{2}}=2}
−
H
L
(
x
,
x
′
)
=
[
0
0
0
−
2
]
{\displaystyle -HL(x,x')={\begin{bmatrix}0&0\\0&-2\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
[ 2]
P5 (a):
J
[
x
]
=
∫
0
40
−
x
˙
2
2
d
t
con
x
(
0
)
=
20
y
x
(
40
)
=
0
.
{\displaystyle {\text{P5 (a): }}J[x]=\int _{0}^{40}-{{\dot {x}}^{2} \over 2}dt\quad {\text{con}}\quad x(0)=20\quad {\text{y}}\quad x(40)=0{\text{.}}}
L
(
t
,
x
,
x
˙
)
=
−
x
˙
2
2
{\displaystyle L(t,x,{\dot {x}})=-{{\dot {x}}^{2} \over 2}}
∂
L
∂
x
(
t
,
x
,
x
˙
)
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})=0}
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
=
−
x
˙
{\displaystyle {\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})=-{\dot {x}}}
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
−
x
¨
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=-{\ddot {x}}}
Equação de Euler
∂
L
∂
x
(
t
,
x
,
x
˙
)
−
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=0}
0
−
(
−
x
¨
)
=
0
→
x
¨
(
t
)
=
0
{\displaystyle 0-(-{\ddot {x}})=0\rightarrow \color {blue}{\ddot {x}}(t)=0}
Integrando
x
¨
(
t
)
{\displaystyle {\ddot {x}}(t)}
x
˙
(
t
)
{\displaystyle {\dot {x}}(t)}
x
˙
(
t
)
=
k
1
{\displaystyle {\dot {x}}(t)=k_{1}}
x
(
t
)
=
k
1
t
+
k
2
{\displaystyle x(t)=k_{1}t+k_{2}}
x
(
0
)
=
k
1
⋅
0
+
k
2
=
20
→
k
2
=
20
{\displaystyle x(0)=k_{1}\cdot 0+k_{2}=20\rightarrow k_{2}=20}
x
(
40
)
=
k
1
⋅
40
+
k
2
=
0
→
k
1
=
−
20
40
=
−
1
2
{\displaystyle x(40)=k_{1}\cdot 40+k_{2}=0\rightarrow k_{1}=-{20 \over 40}=-{1 \over 2}}
x
(
t
)
=
−
1
2
t
+
20
{\displaystyle \color {blue}x(t)=-{1 \over 2}t+20}
Concavidade
∂
2
L
∂
x
2
=
∂
2
L
∂
x
∂
x
˙
=
∂
2
L
∂
x
˙
∂
x
=
0
{\displaystyle {\partial ^{2}L \over \partial x^{2}}={\partial ^{2}L \over \partial x\partial {\dot {x}}}={\partial ^{2}L \over \partial {\dot {x}}\partial x}=0}
∂
2
L
∂
x
˙
2
=
−
1
{\displaystyle {\partial ^{2}L \over \partial {\dot {x}}^{2}}=-1}
−
H
L
(
x
,
x
˙
)
=
[
0
0
0
1
]
{\displaystyle -HL(x,{\dot {x}})={\begin{bmatrix}0&0\\0&1\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
P5 (b):
J
[
x
]
=
∫
0
10
−
(
2
x
x
˙
+
x
˙
2
)
d
t
con
x
(
0
)
=
10
y
x
(
10
)
=
100
.
{\displaystyle {\text{P5 (b): }}J[x]=\int _{0}^{10}-(2x{\dot {x}}+{\dot {x}}^{2})dt\quad {\text{con}}\quad x(0)=10\quad {\text{y}}\quad x(10)=100{\text{.}}}
L
(
t
,
x
,
x
˙
)
=
−
2
x
x
˙
−
x
˙
2
{\displaystyle L(t,x,{\dot {x}})=-2x{\dot {x}}-{\dot {x}}^{2}}
∂
L
∂
x
(
t
,
x
,
x
˙
)
=
−
2
x
˙
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})=-2{\dot {x}}}
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
=
−
2
x
−
2
x
˙
{\displaystyle {\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})=-2x-2{\dot {x}}}
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
−
2
x
˙
−
2
x
¨
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=-2{\dot {x}}-2{\ddot {x}}}
Equação de Euler
∂
L
∂
x
(
t
,
x
,
x
˙
)
−
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=0}
−
2
x
˙
−
(
−
2
x
˙
−
2
x
¨
)
=
0
→
−
2
x
˙
+
2
x
˙
+
2
x
¨
=
0
→
x
¨
(
t
)
=
0
{\displaystyle -2{\dot {x}}-(-2{\dot {x}}-2{\ddot {x}})=0\rightarrow -2{\dot {x}}+2{\dot {x}}+2{\ddot {x}}=0\rightarrow \color {blue}{\ddot {x}}(t)=0}
Integrando
x
¨
(
t
)
{\displaystyle {\ddot {x}}(t)}
x
˙
(
t
)
{\displaystyle {\dot {x}}(t)}
x
˙
(
t
)
=
k
1
{\displaystyle {\dot {x}}(t)=k_{1}}
x
(
t
)
=
k
1
t
+
k
2
{\displaystyle x(t)=k_{1}t+k_{2}}
x
(
0
)
=
k
1
⋅
0
+
k
2
=
10
→
k
2
=
10
{\displaystyle x(0)=k_{1}\cdot 0+k_{2}=10\rightarrow k_{2}=10}
x
(
10
)
=
k
1
⋅
10
+
k
2
=
100
→
k
1
=
100
−
10
10
=
9
{\displaystyle x(10)=k_{1}\cdot 10+k_{2}=100\rightarrow k_{1}={100-10 \over 10}=9}
x
(
t
)
=
9
t
+
10
{\displaystyle \color {blue}x(t)=9t+10}
Concavidade
∂
2
L
∂
x
2
=
0
{\displaystyle {\partial ^{2}L \over \partial x^{2}}=0}
∂
2
L
∂
x
∂
x
˙
=
∂
2
L
∂
x
˙
∂
x
=
−
2
{\displaystyle {\partial ^{2}L \over \partial x\partial {\dot {x}}}={\partial ^{2}L \over \partial {\dot {x}}\partial x}=-2}
∂
2
L
∂
x
˙
2
=
−
2
{\displaystyle {\partial ^{2}L \over \partial {\dot {x}}^{2}}=-2}
−
H
L
(
x
,
x
˙
)
=
[
0
2
2
2
]
{\displaystyle -HL(x,{\dot {x}})={\begin{bmatrix}0&2\\2&2\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
P5 (c):
J
[
x
]
=
∫
0
2
(
12
t
x
+
x
˙
2
)
d
t
con
x
(
0
)
=
1
y
x
(
2
)
=
17
.
{\displaystyle {\text{P5 (c): }}J[x]=\int _{0}^{2}(12tx+{\dot {x}}^{2})dt\quad {\text{con}}\quad x(0)=1\quad {\text{y}}\quad x(2)=17{\text{.}}}
L
(
t
,
x
,
x
˙
)
=
12
t
x
+
x
˙
2
{\displaystyle L(t,x,{\dot {x}})=12tx+{\dot {x}}^{2}}
∂
L
∂
x
(
t
,
x
,
x
˙
)
=
12
t
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})=12t}
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
=
2
x
˙
{\displaystyle {\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})=2{\dot {x}}}
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
2
x
¨
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=2{\ddot {x}}}
Equação de Euler
∂
L
∂
x
(
t
,
x
,
x
˙
)
−
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=0}
12
t
−
2
x
¨
=
0
→
x
¨
(
t
)
=
6
t
{\displaystyle 12t-2{\ddot {x}}=0\rightarrow \color {blue}{\ddot {x}}(t)=6t}
Integrando
x
¨
(
t
)
{\displaystyle {\ddot {x}}(t)}
x
˙
(
t
)
{\displaystyle {\dot {x}}(t)}
x
˙
(
t
)
=
3
t
2
+
k
1
{\displaystyle {\dot {x}}(t)=3t^{2}+k_{1}}
x
(
t
)
=
t
3
+
k
1
t
+
k
2
{\displaystyle x(t)=t^{3}+k_{1}t+k_{2}}
x
(
0
)
=
0
3
+
k
1
⋅
0
+
k
2
=
1
→
k
2
=
1
{\displaystyle x(0)=0^{3}+k_{1}\cdot 0+k_{2}=1\rightarrow k_{2}=1}
x
(
2
)
=
2
3
+
k
1
⋅
2
+
k
2
=
17
→
k
1
=
17
−
8
−
1
2
=
4
{\displaystyle x(2)=2^{3}+k_{1}\cdot 2+k_{2}=17\rightarrow k_{1}={17-8-1 \over 2}=4}
x
(
t
)
=
t
3
+
4
t
+
1
{\displaystyle \color {blue}x(t)=t^{3}+4t+1}
Concavidade
∂
2
L
∂
x
2
=
∂
2
L
∂
x
∂
x
˙
=
∂
2
L
∂
x
˙
∂
x
=
0
{\displaystyle {\partial ^{2}L \over \partial x^{2}}={\partial ^{2}L \over \partial x\partial {\dot {x}}}={\partial ^{2}L \over \partial {\dot {x}}\partial x}=0}
∂
2
L
∂
x
˙
2
=
2
{\displaystyle {\partial ^{2}L \over \partial {\dot {x}}^{2}}=2}
−
H
L
(
x
,
x
˙
)
=
[
0
0
0
−
2
]
{\displaystyle -HL(x,{\dot {x}})={\begin{bmatrix}0&0\\0&-2\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
P5 (d):
J
[
x
]
=
∫
0
2
(
x
+
x
˙
2
)
d
t
con
x
(
0
)
=
1
y
x
(
2
)
=
10
.
{\displaystyle {\text{P5 (d): }}J[x]=\int _{0}^{2}(x+{\dot {x}}^{2})dt\quad {\text{con}}\quad x(0)=1\quad {\text{y}}\quad x(2)=10{\text{.}}}
L
(
t
,
x
,
x
˙
)
=
x
+
x
˙
2
{\displaystyle L(t,x,{\dot {x}})=x+{\dot {x}}^{2}}
∂
L
∂
x
(
t
,
x
,
x
˙
)
=
1
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})=1}
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
=
2
x
˙
{\displaystyle {\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})=2{\dot {x}}}
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
2
x
¨
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=2{\ddot {x}}}
Equação de Euler
∂
L
∂
x
(
t
,
x
,
x
˙
)
−
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=0}
1
−
2
x
¨
=
0
→
x
¨
(
t
)
=
1
2
{\displaystyle 1-2{\ddot {x}}=0\rightarrow \color {blue}{\ddot {x}}(t)={1 \over 2}}
Integrando
x
¨
(
t
)
{\displaystyle {\ddot {x}}(t)}
x
˙
(
t
)
{\displaystyle {\dot {x}}(t)}
x
˙
(
t
)
=
1
2
t
+
k
1
{\displaystyle {\dot {x}}(t)={1 \over 2}t+k_{1}}
x
(
t
)
=
1
4
t
2
+
k
1
t
+
k
2
{\displaystyle x(t)={1 \over 4}t^{2}+k_{1}t+k_{2}}
x
(
0
)
=
1
4
⋅
0
2
+
k
1
⋅
0
+
k
2
=
1
→
k
2
=
1
{\displaystyle x(0)={1 \over 4}\cdot 0^{2}+k_{1}\cdot 0+k_{2}=1\rightarrow k_{2}=1}
x
(
2
)
=
1
4
⋅
2
2
+
k
1
⋅
2
+
k
2
=
10
→
k
1
=
10
−
1
−
1
2
=
8
2
=
4
{\displaystyle x(2)={1 \over 4}\cdot 2^{2}+k_{1}\cdot 2+k_{2}=10\rightarrow k_{1}={10-1-1 \over 2}={8 \over 2}=4}
x
(
t
)
=
1
4
t
2
+
4
t
+
1
{\displaystyle \color {blue}x(t)={1 \over 4}t^{2}+4t+1}
Concavidade
∂
2
L
∂
x
2
=
∂
2
L
∂
x
∂
x
˙
=
∂
2
L
∂
x
˙
∂
x
=
0
{\displaystyle {\partial ^{2}L \over \partial x^{2}}={\partial ^{2}L \over \partial x\partial {\dot {x}}}={\partial ^{2}L \over \partial {\dot {x}}\partial x}=0}
∂
2
L
∂
x
˙
2
=
2
{\displaystyle {\partial ^{2}L \over \partial {\dot {x}}^{2}}=2}
−
H
L
(
x
,
x
˙
)
=
[
0
0
0
−
2
]
{\displaystyle -HL(x,{\dot {x}})={\begin{bmatrix}0&0\\0&-2\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
P5 (e):
J
[
x
]
=
∫
0
2
(
x
2
+
t
2
x
˙
)
d
t
con
x
(
0
)
=
0
y
x
(
2
)
=
2
.
{\displaystyle {\text{P5 (e): }}J[x]=\int _{0}^{2}(x^{2}+t^{2}{\dot {x}})dt\quad {\text{con}}\quad x(0)=0\quad {\text{y}}\quad x(2)=2{\text{.}}}
L
(
t
,
x
,
x
˙
)
=
x
2
+
t
2
x
˙
{\displaystyle L(t,x,{\dot {x}})=x^{2}+t^{2}{\dot {x}}}
∂
L
∂
x
(
t
,
x
,
x
˙
)
=
2
x
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})=2x}
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
=
t
2
{\displaystyle {\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})=t^{2}}
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
2
t
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=2t}
Equação de Euler
∂
L
∂
x
(
t
,
x
,
x
˙
)
−
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=0}
2
x
−
2
t
=
0
→
x
(
t
)
=
t
{\displaystyle 2x-2t=0\rightarrow \color {blue}x(t)=t}
Concavidade
∂
2
L
∂
x
2
=
2
{\displaystyle {\partial ^{2}L \over \partial x^{2}}=2}
∂
2
L
∂
x
∂
x
˙
=
∂
2
L
∂
x
˙
∂
x
=
∂
2
L
∂
x
˙
2
=
0
{\displaystyle {\partial ^{2}L \over \partial x\partial {\dot {x}}}={\partial ^{2}L \over \partial {\dot {x}}\partial x}={\partial ^{2}L \over \partial {\dot {x}}^{2}}=0}
−
H
L
(
x
,
x
˙
)
=
[
−
2
0
0
0
]
{\displaystyle -HL(x,{\dot {x}})={\begin{bmatrix}-2&0\\0&0\end{bmatrix}}}
L
−
{\displaystyle L_{-}}
∴
{\displaystyle \therefore }
x
(
t
)
{\displaystyle x(t)}
P5 (f):
J
[
x
,
y
]
=
∫
0
T
(
2
x
y
−
2
x
2
−
x
˙
2
+
y
˙
2
)
d
t
encontrar únicamente la solución general.
{\displaystyle {\text{P5 (f): }}J[x,y]=\int _{0}^{T}(2xy-2x^{2}-{\dot {x}}^{2}+{\dot {y}}^{2})dt\quad {\text{encontrar únicamente la solución general.}}}
L
(
z
)
=
L
(
t
,
x
,
x
˙
,
y
,
y
˙
)
=
2
x
y
−
2
x
2
−
x
˙
2
+
y
˙
2
{\displaystyle L(z)=L(t,x,{\dot {x}},y,{\dot {y}})=2xy-2x^{2}-{\dot {x}}^{2}+{\dot {y}}^{2}}
∂
L
∂
z
=
[
∂
L
∂
x
∂
L
∂
y
]
=
[
2
y
−
4
x
2
x
]
{\displaystyle {\partial L \over \partial z}={\begin{bmatrix}{\partial L \over \partial x}\\{\partial L \over \partial y}\end{bmatrix}}={\begin{bmatrix}2y-4x\\2x\end{bmatrix}}}
∂
L
∂
z
˙
=
[
∂
L
∂
x
˙
∂
L
∂
y
˙
]
=
[
−
2
x
˙
2
y
˙
]
{\displaystyle {\partial L \over \partial {\dot {z}}}={\begin{bmatrix}{\partial L \over \partial {\dot {x}}}\\{\partial L \over \partial {\dot {y}}}\end{bmatrix}}={\begin{bmatrix}-2{\dot {x}}\\2{\dot {y}}\end{bmatrix}}}
d
d
t
[
∂
L
∂
z
˙
]
=
[
−
2
x
¨
2
y
¨
]
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {z}}}\right]={\begin{bmatrix}-2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}}
Equação de Euler
∂
L
∂
z
(
t
,
x
,
x
˙
,
y
,
y
˙
)
−
d
d
t
[
∂
L
∂
z
˙
(
t
,
x
,
x
˙
,
y
,
y
˙
)
]
=
0
{\displaystyle {\partial L \over \partial z}(t,x,{\dot {x}},y,{\dot {y}})-{d \over dt}\left[{\partial L \over \partial {\dot {z}}}(t,x,{\dot {x}},y,{\dot {y}})\right]=0}
[
2
y
−
4
x
2
x
]
−
[
−
2
x
¨
2
y
¨
]
=
[
0
0
]
→
{
2
y
(
t
)
−
4
x
(
t
)
+
2
x
¨
(
t
)
=
0
2
x
(
t
)
−
2
y
¨
(
t
)
=
0
{\displaystyle {\begin{bmatrix}2y-4x\\2x\end{bmatrix}}-{\begin{bmatrix}-2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}\rightarrow \left\{\color {blue}{\begin{matrix}2y(t)-4x(t)+2{\ddot {x}}(t)=0\\2x(t)-2{\ddot {y}}(t)=0\end{matrix}}\right.}
−
y
¨
+
x
=
0
→
y
¨
(
t
)
=
x
(
t
)
{\displaystyle -{\ddot {y}}+x=0\rightarrow {\ddot {y}}(t)=x(t)}
x
¨
−
2
x
+
y
=
0
→
elevando a +2 em derivadas
→
x
¨
¨
−
2
x
¨
+
y
¨
=
0
{\displaystyle {\ddot {x}}-2x+y=0\rightarrow {\text{elevando a +2 em derivadas}}\rightarrow {\ddot {\ddot {x}}}-2{\ddot {x}}+{\ddot {y}}=0}
substituindo
y
¨
(
t
)
por
x
(
t
)
→
x
¨
¨
(
t
)
−
2
x
¨
(
t
)
+
x
(
t
)
=
0
{\displaystyle {\text{substituindo }}{\ddot {y}}(t){\text{ por }}x(t)\rightarrow {\ddot {\ddot {x}}}(t)-2{\ddot {x}}(t)+x(t)=0}
Substituir
x
n
{\displaystyle x^{n}}
λ
m
{\displaystyle \lambda ^{m}}
n
{\displaystyle n}
m
{\displaystyle m}
λ
4
−
2
λ
2
+
λ
0
=
0
→
λ
4
−
2
λ
2
+
1
=
0
{\displaystyle \lambda ^{4}-2\lambda ^{2}+\lambda ^{0}=0\rightarrow \lambda ^{4}-2\lambda ^{2}+1=0}
Substituir
λ
2
{\displaystyle \lambda ^{2}}
r
{\displaystyle r}
r
2
−
2
r
+
1
=
0
→
r
=
2
±
4
−
4
⋅
1
⋅
1
2
=
1
→
λ
2
=
r
→
λ
=
±
1
{\displaystyle r^{2}-2r+1=0\rightarrow r={2\pm {\sqrt {4-4\cdot 1\cdot 1}} \over 2}=1\rightarrow \lambda ^{2}=r\rightarrow \lambda =\pm 1}
x
(
t
)
=
k
1
e
t
+
k
2
t
e
t
+
k
3
e
−
t
+
k
4
t
e
−
t
{\displaystyle \color {blue}x(t)=k_{1}e^{t}+k_{2}te^{t}+k_{3}e^{-t}+k_{4}te^{-t}}
y
¨
(
t
)
=
x
(
t
)
=
k
1
e
t
+
k
2
t
e
t
+
k
3
e
−
t
+
k
4
t
e
−
t
{\displaystyle {\ddot {y}}(t)=x(t)=k_{1}e^{t}+k_{2}te^{t}+k_{3}e^{-t}+k_{4}te^{-t}}
y
˙
(
t
)
=
k
1
e
t
+
k
2
(
t
−
1
)
e
t
−
k
3
e
−
t
−
k
4
(
t
+
1
)
e
−
t
+
c
1
{\displaystyle {\dot {y}}(t)=k_{1}e^{t}+k_{2}(t-1)e^{t}-k_{3}e^{-t}-k_{4}(t+1)e^{-t}+c_{1}}
y
(
t
)
=
k
1
e
t
+
k
2
(
t
−
2
)
e
t
+
k
3
e
−
t
+
k
4
(
t
+
2
)
e
−
t
+
c
1
t
+
c
2
{\displaystyle \color {blue}y(t)=k_{1}e^{t}+k_{2}(t-2)e^{t}+k_{3}e^{-t}+k_{4}(t+2)e^{-t}+c_{1}t+c_{2}}
P5 (g):
J
[
x
,
y
]
=
∫
0
10
(
x
˙
2
+
y
˙
2
+
e
t
)
d
t
dadas
x
(
0
)
=
0
,
y
(
0
)
=
2
,
x
(
10
)
=
11
y
y
(
10
)
=
6
.
{\displaystyle {\text{P5 (g): }}J[x,y]=\int _{0}^{10}({\dot {x}}^{2}+{\dot {y}}^{2}+e^{t})dt\quad {\text{dadas}}\quad x(0)=0\quad {\text{,}}\quad y(0)=2\quad {\text{,}}\quad x(10)=11\quad {\text{y}}\quad y(10)=6{\text{.}}}
L
(
z
)
=
L
(
t
,
x
,
x
˙
,
y
,
y
˙
)
=
x
˙
2
+
y
˙
2
+
e
t
{\displaystyle L(z)=L(t,x,{\dot {x}},y,{\dot {y}})={\dot {x}}^{2}+{\dot {y}}^{2}+e^{t}}
∂
L
∂
z
=
[
∂
L
∂
x
∂
L
∂
y
]
=
[
0
0
]
{\displaystyle {\partial L \over \partial z}={\begin{bmatrix}{\partial L \over \partial x}\\{\partial L \over \partial y}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}}
∂
L
∂
z
˙
=
[
∂
L
∂
x
˙
∂
L
∂
y
˙
]
=
[
2
x
˙
2
y
˙
]
{\displaystyle {\partial L \over \partial {\dot {z}}}={\begin{bmatrix}{\partial L \over \partial {\dot {x}}}\\{\partial L \over \partial {\dot {y}}}\end{bmatrix}}={\begin{bmatrix}2{\dot {x}}\\2{\dot {y}}\end{bmatrix}}}
d
d
t
[
∂
L
∂
z
˙
]
=
[
2
x
¨
2
y
¨
]
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {z}}}\right]={\begin{bmatrix}2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}}
Equação de Euler
∂
L
∂
z
(
t
,
x
,
x
˙
,
y
,
y
˙
)
−
d
d
t
[
∂
L
∂
z
˙
(
t
,
x
,
x
˙
,
y
,
y
˙
)
]
=
0
{\displaystyle {\partial L \over \partial z}(t,x,{\dot {x}},y,{\dot {y}})-{d \over dt}\left[{\partial L \over \partial {\dot {z}}}(t,x,{\dot {x}},y,{\dot {y}})\right]=0}
[
0
0
]
−
[
2
x
¨
2
y
¨
]
=
[
0
0
]
→
{
−
2
x
¨
(
t
)
=
0
−
2
y
¨
(
t
)
=
0
{\displaystyle {\begin{bmatrix}0\\0\end{bmatrix}}-{\begin{bmatrix}2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}\rightarrow \left\{\color {blue}{\begin{matrix}-2{\ddot {x}}(t)=0\\-2{\ddot {y}}(t)=0\end{matrix}}\right.}
x
¨
(
t
)
=
0
→
x
˙
(
t
)
=
k
1
→
x
(
t
)
=
k
1
t
+
k
2
{\displaystyle {\ddot {x}}(t)=0\rightarrow {\dot {x}}(t)=k_{1}\rightarrow x(t)=k_{1}t+k_{2}}
y
¨
(
t
)
=
0
→
y
˙
(
t
)
=
c
1
→
y
(
t
)
=
c
1
t
+
c
2
{\displaystyle {\ddot {y}}(t)=0\rightarrow {\dot {y}}(t)=c_{1}\rightarrow y(t)=c_{1}t+c_{2}}
x
(
0
)
=
k
1
⋅
0
+
k
2
=
0
→
k
2
=
0
{\displaystyle x(0)=k_{1}\cdot 0+k_{2}=0\rightarrow k_{2}=0}
x
(
10
)
=
k
1
⋅
10
+
k
2
=
11
→
k
1
=
11
−
0
10
=
11
10
{\displaystyle x(10)=k_{1}\cdot 10+k_{2}=11\rightarrow k_{1}={11-0 \over 10}={11 \over 10}}
x
(
t
)
=
11
10
t
{\displaystyle \color {blue}x(t)={11 \over 10}t}
y
(
0
)
=
c
1
⋅
0
+
c
2
=
2
→
c
2
=
2
{\displaystyle y(0)=c_{1}\cdot 0+c_{2}=2\rightarrow c_{2}=2}
y
(
10
)
=
c
1
⋅
10
+
c
2
=
6
→
c
1
=
6
−
2
10
=
2
5
{\displaystyle y(10)=c_{1}\cdot 10+c_{2}=6\rightarrow c_{1}={6-2 \over 10}={2 \over 5}}
y
(
t
)
=
2
5
t
+
2
{\displaystyle \color {blue}y(t)={2 \over 5}t+2}
P5 (h):
J
[
x
,
y
]
=
∫
0
π
2
(
x
˙
2
+
y
˙
2
+
2
x
y
)
d
t
dadas
x
(
0
)
=
y
(
0
)
=
0
y
x
(
π
2
)
=
y
(
π
2
)
=
1
.
{\displaystyle {\text{P5 (h): }}J[x,y]=\int _{0}^{\pi \over 2}({\dot {x}}^{2}+{\dot {y}}^{2}+2xy)dt\quad {\text{dadas}}\quad x(0)=y(0)=0\quad {\text{y}}\quad x\left({\pi \over 2}\right)=y\left({\pi \over 2}\right)=1{\text{.}}}
L
(
z
)
=
L
(
t
,
x
,
x
˙
,
y
,
y
˙
)
=
x
˙
2
+
y
˙
2
+
2
x
y
{\displaystyle L(z)=L(t,x,{\dot {x}},y,{\dot {y}})={\dot {x}}^{2}+{\dot {y}}^{2}+2xy}
∂
L
∂
z
=
[
∂
L
∂
x
∂
L
∂
y
]
=
[
2
y
2
x
]
{\displaystyle {\partial L \over \partial z}={\begin{bmatrix}{\partial L \over \partial x}\\{\partial L \over \partial y}\end{bmatrix}}={\begin{bmatrix}2y\\2x\end{bmatrix}}}
∂
L
∂
z
˙
=
[
∂
L
∂
x
˙
∂
L
∂
y
˙
]
=
[
2
x
˙
2
y
˙
]
{\displaystyle {\partial L \over \partial {\dot {z}}}={\begin{bmatrix}{\partial L \over \partial {\dot {x}}}\\{\partial L \over \partial {\dot {y}}}\end{bmatrix}}={\begin{bmatrix}2{\dot {x}}\\2{\dot {y}}\end{bmatrix}}}
d
d
t
[
∂
L
∂
z
˙
]
=
[
2
x
¨
2
y
¨
]
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {z}}}\right]={\begin{bmatrix}2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}}
Equação de Euler
∂
L
∂
z
(
t
,
x
,
x
˙
,
y
,
y
˙
)
−
d
d
t
[
∂
L
∂
z
˙
(
t
,
x
,
x
˙
,
y
,
y
˙
)
]
=
0
{\displaystyle {\partial L \over \partial z}(t,x,{\dot {x}},y,{\dot {y}})-{d \over dt}\left[{\partial L \over \partial {\dot {z}}}(t,x,{\dot {x}},y,{\dot {y}})\right]=0}
[
2
y
2
x
]
−
[
2
x
¨
2
y
¨
]
=
[
0
0
]
→
{
−
x
¨
(
t
)
+
y
(
t
)
=
0
−
y
¨
(
t
)
+
x
(
t
)
=
0
{\displaystyle {\begin{bmatrix}2y\\2x\end{bmatrix}}-{\begin{bmatrix}2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}\rightarrow \left\{\color {blue}{\begin{matrix}-{\ddot {x}}(t)+y(t)=0\\-{\ddot {y}}(t)+x(t)=0\end{matrix}}\right.}
−
x
¨
+
y
=
0
→
elevando a +2 em derivadas
→
−
x
¨
¨
+
y
¨
=
0
→
−
x
¨
¨
+
x
=
0
{\displaystyle -{\ddot {x}}+y=0\rightarrow {\text{elevando a +2 em derivadas}}\rightarrow -{\ddot {\ddot {x}}}+{\ddot {y}}=0\rightarrow -{\ddot {\ddot {x}}}+x=0}
Substituir
x
n
{\displaystyle x^{n}}
λ
m
{\displaystyle \lambda ^{m}}
n
{\displaystyle n}
m
{\displaystyle m}
−
λ
4
+
λ
0
=
0
→
−
λ
4
+
1
=
0
→
λ
4
=
1
→
λ
=
±
1
ou
±
i
{\displaystyle -\lambda ^{4}+\lambda ^{0}=0\rightarrow -\lambda ^{4}+1=0\rightarrow \lambda ^{4}=1\rightarrow \lambda =\pm 1{\text{ ou }}\pm i}
x
(
t
)
=
k
1
e
t
+
k
2
e
−
t
+
k
3
cos
t
−
k
4
sen
t
{\displaystyle \color {red}x(t)=k_{1}e^{t}+k_{2}e^{-t}+k_{3}\cos t-k_{4}\operatorname {sen} t}
y
¨
=
x
(
t
)
=
k
1
e
t
+
k
2
e
−
t
+
k
3
cos
t
−
k
4
sen
t
{\displaystyle \color {red}{\ddot {y}}=x(t)=k_{1}e^{t}+k_{2}e^{-t}+k_{3}\cos t-k_{4}\operatorname {sen} t}
y
˙
=
k
1
e
t
−
k
2
e
−
t
+
k
3
sen
t
+
k
4
cos
t
+
c
1
{\displaystyle \color {red}{\dot {y}}=k_{1}e^{t}-k_{2}e^{-t}+k_{3}\operatorname {sen} t+k_{4}\cos t+c_{1}}
y
(
t
)
=
k
1
e
t
+
k
2
e
−
t
−
k
3
cos
t
+
k
4
sen
t
+
c
1
t
+
c
2
{\displaystyle \color {red}y(t)=k_{1}e^{t}+k_{2}e^{-t}-k_{3}\cos t+k_{4}\operatorname {sen} t+c_{1}t+c_{2}}
P5 (i):
J
[
x
]
=
∫
0
1
(
1
+
x
¨
2
)
d
t
con
x
(
0
)
=
0
y
x
˙
(
0
)
=
x
(
1
)
=
x
˙
(
1
)
=
1
.
{\displaystyle {\text{P5 (i): }}J[x]=\int _{0}^{1}(1+{\ddot {x}}^{2})dt\quad {\text{con}}\quad x(0)=0\quad {\text{y}}\quad {\dot {x}}(0)=x(1)={\dot {x}}(1)=1{\text{.}}}
L
(
t
,
x
,
x
˙
,
x
¨
)
=
1
+
x
¨
2
{\displaystyle L(t,x,{\dot {x}},{\ddot {x}})=1+{\ddot {x}}^{2}}
∂
L
∂
x
(
t
,
x
,
x
˙
,
x
¨
)
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}},{\ddot {x}})=0}
∂
L
∂
x
˙
(
t
,
x
,
x
˙
,
x
¨
)
=
0
{\displaystyle {\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}},{\ddot {x}})=0}
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
,
x
¨
)
]
=
0
{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]=0}
∂
L
∂
x
¨
(
t
,
x
,
x
˙
,
x
¨
)
=
2
x
¨
{\displaystyle {\partial L \over \partial {\ddot {x}}}(t,x,{\dot {x}},{\ddot {x}})=2{\ddot {x}}}
d
2
d
t
2
[
∂
L
∂
x
¨
(
t
,
x
,
x
˙
,
x
¨
)
]
=
2
x
¨
˙
{\displaystyle {d^{2} \over dt^{2}}\left[{\partial L \over \partial {\ddot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]=2{\dot {\ddot {x}}}}
Equação de Euler-Poisson
∂
L
∂
x
(
t
,
x
,
x
˙
,
x
¨
)
−
d
d
t
[
∂
L
∂
x
˙
(
t
,
x
,
x
˙
,
x
¨
)
]
+
d
2
d
t
2
[
∂
L
∂
x
¨
(
t
,
x
,
x
˙
,
x
¨
)
]
=
0
{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}},{\ddot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]+{d^{2} \over dt^{2}}\left[{\partial L \over \partial {\ddot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]=0}
0
−
0
+
2
x
¨
˙
=
0
→
x
¨
˙
=
0
{\displaystyle 0-0+2{\dot {\ddot {x}}}=0\rightarrow \color {blue}{\dot {\ddot {x}}}=0}
Integrando
x
¨
˙
(
t
)
{\displaystyle {\dot {\ddot {x}}}(t)}
x
¨
(
t
)
{\displaystyle {\ddot {x}}(t)}
x
˙
(
t
)
{\displaystyle {\dot {x}}(t)}
x
¨
˙
(
t
)
=
0
→
∫
0
1
(
x
¨
˙
(
t
)
)
d
t
=
∫
0
1
(
0
)
d
t
→
x
¨
(
t
)
=
k
1
{\displaystyle {\dot {\ddot {x}}}(t)=0\rightarrow \int _{0}^{1}({\dot {\ddot {x}}}(t))dt=\int _{0}^{1}(0)dt\rightarrow {\ddot {x}}(t)=k_{1}}
x
˙
(
t
)
=
k
1
t
+
k
2
{\displaystyle {\dot {x}}(t)=k_{1}t+k_{2}}
x
(
t
)
=
k
1
2
t
2
+
k
2
t
+
k
3
{\displaystyle x(t)={k_{1} \over 2}t^{2}+k_{2}t+k_{3}}
Substituindo as condições iniciais.
x
(
0
)
=
k
1
2
⋅
0
2
+
k
2
⋅
0
+
k
3
=
0
→
k
3
=
0
{\displaystyle x(0)={k_{1} \over 2}\cdot 0^{2}+k_{2}\cdot 0+k_{3}=0\rightarrow k_{3}=0}
x
˙
(
0
)
=
k
1
⋅
0
+
k
2
=
1
→
k
2
=
1
{\displaystyle {\dot {x}}(0)=k_{1}\cdot 0+k_{2}=1\rightarrow k_{2}=1}
x
(
1
)
=
k
1
2
⋅
1
2
+
k
2
⋅
1
+
k
3
=
1
→
k
1
=
(
1
−
1
−
0
)
⋅
2
=
0
{\displaystyle x(1)={k_{1} \over 2}\cdot 1^{2}+k_{2}\cdot 1+k_{3}=1\rightarrow k_{1}=(1-1-0)\cdot 2=0}
x
(
t
)
=
0
2
t
2
+
1
⋅
t
+
0
=
t
{\displaystyle {\color {blue}x(t)}={0 \over 2}t^{2}+1\cdot t+0={\color {blue}t}}
Ainda há mais uma condição que não precisou ser utilizada para chegar ao extremal. Entretanto, podemos substituir a condição no extremal encontrado para ver se é atendida.
x
˙
(
1
)
=
k
1
⋅
1
+
k
2
=
1
→
k
2
=
1
{\displaystyle {\dot {x}}(1)=k_{1}\cdot 1+k_{2}=1\rightarrow k_{2}=1}
1. Halle las sendas óptimas
u
∗
(
t
)
{\displaystyle u^{*}(t)}
y
∗
(
t
)
{\displaystyle y^{*}(t)}
λ
∗
(
t
)
{\displaystyle \lambda ^{*}(t)}
a.
max
V
=
∫
0
2
(
3
y
(
t
)
−
2
u
(
t
)
2
)
d
t
{\displaystyle V=\int _{0}^{2}(3y(t)-2u(t)^{2})dt}
s.a
y
′
(
t
)
=
3
u
(
t
)
−
1
{\displaystyle y'(t)=3u(t)-1}
y
(
0
)
=
1
{\displaystyle y(0)=1}
y
(
2
)
=
y
2
(
libre
)
{\displaystyle y(2)=y_{2}({\text{libre}})}
Construir Hamiltoniano.
H
(
t
,
λ
(
t
)
,
u
(
t
)
,
y
(
t
)
)
=
f
(
t
,
y
(
t
)
,
u
(
t
)
)
+
λ
(
t
)
⋅
g
(
t
,
y
(
t
)
,
u
(
t
)
)
{\displaystyle H(t,\lambda (t),u(t),y(t))=f(t,y(t),u(t))+\lambda (t)\cdot g(t,y(t),u(t))}
H
(
t
,
λ
(
t
)
,
u
(
t
)
,
y
(
t
)
)
=
3
y
(
t
)
−
2
u
(
t
)
2
+
λ
(
t
)
⋅
(
3
u
(
t
)
−
1
)
{\displaystyle H(t,\lambda (t),u(t),y(t))=3y(t)-2u(t)^{2}+\lambda (t)\cdot (3u(t)-1)}
Princípio do Ótimo de Pontryagin (condição necessária de H).
∂
H
∂
u
(
t
)
=
−
4
u
(
t
)
+
3
λ
(
t
)
=
0
→
u
∗
(
t
)
=
3
4
λ
(
t
)
{\displaystyle {\partial H \over \partial u(t)}=-4u(t)+3\lambda (t)=0\rightarrow u^{*}(t)={3 \over 4}\lambda (t)}
As equações do movimento do problema.
y
′
(
t
)
=
∂
H
∂
λ
(
t
)
=
3
u
(
t
)
−
1
{\displaystyle y'(t)={\partial H \over \partial \lambda (t)}=3u(t)-1}
λ
′
(
t
)
=
−
∂
H
∂
y
(
t
)
=
−
3
→
integrar
λ
′
(
t
)
→
λ
(
t
)
=
∫
0
2
(
−
3
)
d
t
=
−
3
t
+
k
1
{\displaystyle \lambda '(t)=-{\partial H \over \partial y(t)}=-3\rightarrow {\text{ integrar }}\lambda '(t)\rightarrow \lambda (t)=\int _{0}^{2}(-3)dt=-3t+k_{1}}
Encontrar a constante
k
1
{\displaystyle k_{1}}
H
(
t
)
⋅
d
t
−
λ
(
t
)
⋅
d
y
(
t
)
=
0
{\displaystyle H(t)\cdot dt-\lambda (t)\cdot dy(t)=0}
Quando o tempo final
t
{\displaystyle t}
(
∂
H
∂
t
=
0
)
{\displaystyle \left({\partial H \over \partial t}=0\right)\,}
H
(
x
∗
(
t
)
,
u
∗
(
t
)
,
λ
∗
(
t
)
)
=
constante
{\displaystyle H(x^{*}(t),u^{*}(t),\lambda ^{*}(t))={\text{constante}}}
t
{\displaystyle t}
H
(
x
∗
(
t
)
,
u
∗
(
t
)
,
λ
∗
(
t
)
)
=
0
{\displaystyle H(x^{*}(t),u^{*}(t),\lambda ^{*}(t))=0}
H
(
t
)
⋅
d
t
−
λ
(
t
)
⋅
d
y
(
t
)
=
0
→
−
λ
(
t
)
⋅
d
y
(
t
)
=
0
{\displaystyle {\cancel {H(t)\cdot dt}}-\lambda (t)\cdot dy(t)=0\rightarrow -\lambda (t)\cdot dy(t)=0}
Para que a variação
d
y
(
t
)
{\displaystyle dy(t)}
λ
(
t
)
=
0
{\displaystyle \lambda (t)=0}
λ
(
2
)
=
0
→
−
3
t
+
k
1
=
0
→
k
1
=
6
→
λ
∗
(
t
)
=
−
3
t
+
6
{\displaystyle \lambda (2)=0\rightarrow -3t+k_{1}=0\rightarrow k_{1}=6\rightarrow \color {blue}\lambda ^{*}(t)=-3t+6}
Substituir
λ
∗
(
t
)
{\displaystyle \lambda ^{*}(t)}
u
∗
(
t
)
{\displaystyle u^{*}(t)}
u
∗
(
t
)
=
3
4
λ
∗
(
t
)
=
3
4
⋅
(
−
3
t
+
6
)
=
−
9
t
+
18
4
{\displaystyle {\color {blue}u^{*}(t)}={3 \over 4}\lambda ^{*}(t)={3 \over 4}\cdot (-3t+6)=\color {blue}{-9t+18 \over 4}}
Substituir
u
∗
(
t
)
{\displaystyle u^{*}(t)}
y
′
(
t
)
{\displaystyle y'(t)}
y
′
(
t
)
=
3
u
∗
(
t
)
−
1
=
3
⋅
(
−
9
t
+
18
4
)
−
1
=
−
27
t
+
54
4
−
1
=
−
27
t
+
50
4
=
−
1
4
⋅
(
27
t
−
50
)
{\displaystyle y'(t)=3u^{*}(t)-1=3\cdot \left({-9t+18 \over 4}\right)-1={-27t+54 \over 4}-1={-27t+50 \over 4}=-{1 \over 4}\cdot (27t-50)}
Integrar
y
′
(
t
)
{\displaystyle y'(t)}
y
∗
(
t
)
=
∫
0
2
(
y
′
(
t
)
)
d
t
=
−
1
4
⋅
∫
0
2
(
27
t
−
50
)
d
t
=
−
1
4
(
27
t
2
2
−
50
t
+
k
2
)
=
−
27
t
2
8
+
50
t
4
−
k
2
4
{\displaystyle y^{*}(t)=\int _{0}^{2}(y'(t))dt=-{1 \over 4}\cdot \int _{0}^{2}(27t-50)dt=-{1 \over 4}\left({27t^{2} \over 2}-50t+k_{2}\right)=-{27t^{2} \over 8}+{50t \over 4}-{k_{2} \over 4}}
Usar as condições iniciais do problema para achar a constante
k
2
{\displaystyle k_{2}}
y
(
0
)
=
−
27
⋅
0
2
8
+
50
⋅
0
4
−
k
2
4
=
1
→
k
2
=
−
4
{\displaystyle y(0)=-{27\cdot 0^{2} \over 8}+{50\cdot 0 \over 4}-{k_{2} \over 4}=1\rightarrow k_{2}=-4}
y
∗
(
t
)
=
−
27
t
2
8
+
50
t
4
+
1
{\displaystyle \color {blue}y^{*}(t)=-{27t^{2} \over 8}+{50t \over 4}+1}
Montar a Hessiana para ver se a função Hamiltoniano é côncava. Se sim, então
λ
∗
(
t
)
{\displaystyle \lambda ^{*}(t)}
u
∗
(
t
)
{\displaystyle u^{*}(t)}
y
∗
(
t
)
{\displaystyle y^{*}(t)}
−
Hessiana
=
[
∂
2
H
∂
u
(
t
)
2
∂
2
H
∂
y
(
t
)
∂
u
(
t
)
∂
2
H
∂
u
(
t
)
∂
y
(
t
)
∂
2
H
∂
y
(
t
)
2
]
=
−
[
−
4
0
0
0
]
{\displaystyle -{\text{Hessiana}}={\begin{bmatrix}{\partial ^{2}H \over \partial u(t)^{2}}&{\partial ^{2}H \over \partial y(t)\partial u(t)}\\{\partial ^{2}H \over \partial u(t)\partial y(t)}&{\partial ^{2}H \over \partial y(t)^{2}}\end{bmatrix}}=-{\begin{bmatrix}-4&0\\0&0\end{bmatrix}}}
H
1
<
0
H
2
=
0
}
−
H
1
>
0
−
H
2
=
0
}
{\displaystyle \left.{\begin{matrix}H1<0\\H2=0\end{matrix}}\right\}\left.{\begin{matrix}-H1>0\\-H2=0\end{matrix}}\right\}}
∴
{\displaystyle \therefore }
−
H
{\displaystyle -H}
b.
max
V
=
∫
0
1
L
n
(
4
y
u
)
d
t
{\displaystyle V=\int _{0}^{1}Ln(4yu)dt}
s.a
y
′
=
4
y
(
1
−
u
)
{\displaystyle y'=4y(1-u)}
y
(
0
)
=
1
{\displaystyle y(0)=1}
y
(
1
)
=
e
2
{\displaystyle y(1)=e^{2}}
Construir Hamiltoniano.
H
(
t
,
λ
,
u
,
y
)
=
L
n
(
4
y
u
)
+
λ
⋅
4
y
(
1
−
u
)
{\displaystyle H(t,\lambda ,u,y)=Ln(4yu)+\lambda \cdot 4y(1-u)}
Princípio do Ótimo de Pontryagin (condição necessária, mas não suficiente).
∂
H
∂
u
(
t
)
=
(
4
y
u
)
′
4
y
u
−
4
y
λ
=
4
y
4
y
u
−
4
y
λ
=
0
→
u
∗
(
t
)
=
1
4
y
(
t
)
λ
(
t
)
{\displaystyle {\partial H \over \partial u(t)}={(4yu)' \over 4yu}-4y\lambda ={4y \over 4yu}-4y\lambda =0\rightarrow u^{*}(t)={1 \over 4y(t)\lambda (t)}}
As equações do movimento do problema.
y
′
=
∂
H
∂
λ
=
4
y
(
1
−
u
)
{\displaystyle y'={\partial H \over \partial \lambda }=4y(1-u)}
λ
′
=
−
∂
H
∂
y
=
−
(
(
4
y
u
)
′
4
y
u
+
4
λ
−
4
λ
u
)
=
−
1
y
−
4
λ
+
4
λ
⋅
1
4
λ
y
=
−
4
λ
→
integrar
λ
′
→
λ
=
∫
0
1
(
−
4
λ
)
d
t
=
k
1
e
−
4
t
{\displaystyle \lambda '=-{\partial H \over \partial y}=-\left({(4yu)' \over 4yu}+4\lambda -4\lambda u\right)=-{1 \over y}-4\lambda +{\cancel {4\lambda }}\cdot {1 \over {\cancel {4\lambda }}y}=-4\lambda \rightarrow {\text{ integrar }}\lambda '\rightarrow \lambda =\int _{0}^{1}(-4\lambda )dt=k_{1}e^{-4t}}
Substituir
λ
{\displaystyle \lambda }
y
′
{\displaystyle y'}
y
′
=
4
y
(
1
−
u
∗
)
=
4
y
(
1
−
1
4
y
λ
)
=
4
y
−
(
4
y
4
y
⋅
k
1
e
−
4
t
)
=
4
y
−
e
4
t
k
1
{\displaystyle y'=4y(1-u^{*})=4y\left(1-{1 \over 4y\lambda }\right)=4y-\left({{\cancel {4y}} \over {\cancel {4y}}\cdot k_{1}e^{-4t}}\right)=4y-{e^{4t} \over k_{1}}}
Como resolver
x
′
(
t
)
=
a
(
t
)
x
(
t
)
+
b
(
t
)
{\displaystyle x'(t)=a(t)x(t)+b(t)}
Defina
α
(
t
)
=
∫
0
t
a
(
s
)
d
s
{\displaystyle \alpha (t)=\int _{0}^{t}a(s)ds}
x
(
t
)
=
e
α
(
t
)
(
∫
0
t
e
−
α
(
s
)
⋅
b
(
s
)
d
s
+
c
)
{\displaystyle x(t)=e^{\alpha (t)}\left(\int _{0}^{t}e^{-\alpha (s)}\cdot b(s)ds+c\right)}
Verificação
x
′
(
t
)
=
α
′
(
t
)
⋅
e
α
(
t
)
(
∫
0
t
e
−
α
(
t
)
⋅
b
(
s
)
d
s
+
c
)
+
e
α
(
t
)
(
e
−
α
(
t
)
⋅
b
(
t
)
)
=
α
′
(
t
)
x
(
t
)
+
b
(
t
)
{\displaystyle x'(t)=\alpha '(t)\cdot e^{\alpha (t)}\left(\int _{0}^{t}e^{-\alpha (t)}\cdot b(s)ds+c\right)+{\cancel {e^{\alpha (t)}}}\left({\cancel {e^{-\alpha (t)}}}\cdot b(t)\right)=\alpha '(t)x(t)+b(t)}
y
′
(
t
)
=
4
y
−
e
4
t
k
1
a
(
t
)
=
4
b
(
t
)
=
−
e
4
t
k
1
{\displaystyle y'(t)=4y-{e^{4t} \over k_{1}}\qquad a(t)=4\qquad b(t)=-{e^{4t} \over k_{1}}}
α
(
t
)
=
∫
0
t
4
d
s
=
4
s
|
0
t
=
4
t
{\displaystyle \alpha (t)=\int _{0}^{t}4ds=4s{\Big |}_{0}^{t}=4t}
y
(
t
)
=
e
4
t
(
∫
0
t
e
−
4
s
(
−
e
4
s
k
1
)
d
s
+
c
)
=
e
4
t
(
∫
0
t
−
1
k
1
d
s
+
c
)
=
e
4
t
(
−
t
k
1
+
c
)
{\displaystyle y(t)=e^{4t}\left(\int _{0}^{t}{\cancel {e^{-4s}}}\left(-{{\cancel {e^{4s}}} \over k_{1}}\right)ds+c\right)=e^{4t}\left(\int _{0}^{t}-{1 \over k_{1}}ds+c\right)=e^{4t}\left(-{t \over k_{1}}+c\right)}
y
(
0
)
=
e
4
⋅
0
(
−
0
k
1
+
c
)
=
1
→
c
=
1
{\displaystyle y(0)=e^{4\cdot 0}\left(-{0 \over k_{1}}+c\right)=1\rightarrow c=1}
y
(
1
)
=
e
4
⋅
1
(
−
1
k
1
+
1
)
=
e
2
→
e
−
2
=
−
1
+
k
1
k
1
→
k
1
e
−
2
−
k
1
=
−
1
=
k
1
(
e
−
2
−
1
)
→
k
1
=
−
1
e
−
2
−
1
≈
1
,
15652
{\displaystyle y(1)=e^{4\cdot 1}\left(-{1 \over k_{1}}+1\right)=e^{2}\rightarrow e^{-2}={-1+k_{1} \over k_{1}}\rightarrow k_{1}e^{-2}-k_{1}=-1=k_{1}(e^{-2}-1)\rightarrow k_{1}=-{1 \over e^{-2}-1}\approx 1,15652}
Logo:
y
∗
(
t
)
=
e
4
t
(
−
t
k
1
+
c
)
≈
e
4
t
(
−
t
1
,
16
+
1
)
{\displaystyle {\color {blue}y^{*}(t)}=e^{4t}\left(-{t \over k_{1}}+c\right)\approx {\color {blue}e^{4t}\left(-{t \over 1,16}+1\right)}}
λ
∗
(
t
)
=
k
1
e
−
4
t
≈
1
,
16
e
4
t
{\displaystyle {\color {blue}\lambda ^{*}(t)}=k_{1}e^{-4t}\approx {\color {blue}{1,16 \over e^{4t}}}}
u
∗
(
t
)
=
1
4
y
∗
(
t
)
λ
∗
(
t
)
=
1
4
⋅
e
4
t
(
−
t
1
,
16
+
1
)
⋅
1
,
16
e
4
t
≈
1
−
4
t
+
4
,
63
{\displaystyle {\color {blue}u^{*}(t)}={1 \over 4y^{*}(t)\lambda ^{*}(t)}={1 \over 4\cdot {\cancel {e^{4t}}}\left(-{t \over 1,16}+1\right)\cdot {1,16 \over {\cancel {e^{4t}}}}}\approx {\color {blue}{1 \over -4t+4,63}}}
Verificar se a função Hamiltoniana é côncava em relação a
y
{\displaystyle y}
u
{\displaystyle u}
−
Hessiana
=
[
∂
2
H
∂
u
(
t
)
2
∂
2
H
∂
y
(
t
)
∂
u
(
t
)
∂
2
H
∂
u
(
t
)
∂
y
(
t
)
∂
2
H
∂
y
(
t
)
2
]
=
−
[
−
1
u
2
0
0
−
1
y
2
]
{\displaystyle \color {red}-{\text{Hessiana}}={\begin{bmatrix}{\partial ^{2}H \over \partial u(t)^{2}}&{\partial ^{2}H \over \partial y(t)\partial u(t)}\\{\partial ^{2}H \over \partial u(t)\partial y(t)}&{\partial ^{2}H \over \partial y(t)^{2}}\end{bmatrix}}=-{\begin{bmatrix}-{1 \over u^{2}}&0\\0&-{1 \over y^{2}}\end{bmatrix}}}
H
1
<
0
H
2
<
0
}
−
H
1
>
0
−
H
2
>
0
}
{\displaystyle \left.{\begin{matrix}H1<0\\H2<0\end{matrix}}\right\}\left.{\begin{matrix}-H1>0\\-H2>0\end{matrix}}\right\}}
∴
{\displaystyle \therefore }
−
H
{\displaystyle -H}
c.
max
V
=
∫
0
1
−
u
2
d
t
{\displaystyle V=\int _{0}^{1}-u^{2}dt}
s.a
y
′
=
y
+
u
{\displaystyle y'=y+u}
y
(
0
)
=
1
{\displaystyle y(0)=1}
y
(
1
)
=
0
{\displaystyle y(1)=0}
Construir Hamiltoniano.
H
(
t
,
λ
,
u
,
y
)
=
−
u
2
+
λ
⋅
(
y
+
u
)
{\displaystyle H(t,\lambda ,u,y)=-u^{2}+\lambda \cdot (y+u)}
H
{\displaystyle H}
u
{\displaystyle u}
Princípio do Ótimo de Pontryagin (condição necessária de H).
∂
H
∂
u
=
−
2
u
+
λ
=
0
→
u
∗
=
λ
2
{\displaystyle {\partial H \over \partial u}=-2u+\lambda =0\rightarrow u^{*}={\lambda \over 2}}
As equações do movimento do problema.
y
′
=
∂
H
∂
λ
=
y
+
u
{\displaystyle y'={\partial H \over \partial \lambda }=y+u}
λ
′
=
−
∂
H
∂
y
=
−
λ
→
integrar
λ
′
→
λ
∗
(
t
)
=
∫
0
1
(
−
λ
)
d
t
=
k
1
e
−
t
{\displaystyle \lambda '=-{\partial H \over \partial y}=-\lambda \rightarrow {\text{ integrar }}\lambda '\rightarrow \lambda ^{*}(t)=\int _{0}^{1}(-\lambda )dt=k_{1}e^{-t}}
Substituir
λ
∗
(
t
)
{\displaystyle \lambda ^{*}(t)}
u
∗
(
t
)
{\displaystyle u^{*}(t)}
u
∗
(
t
)
=
λ
∗
2
=
k
1
e
−
t
2
{\displaystyle u^{*}(t)={\lambda ^{*} \over 2}={k_{1}e^{-t} \over 2}}
Equação Diferencial Ordinária (Wikibooks , Wikipédia ) (e substituir
u
∗
(
t
)
{\displaystyle u^{*}(t)}
y
′
(
t
)
{\displaystyle y'(t)}
y
′
(
t
)
=
y
(
t
)
+
k
1
e
−
t
2
a
(
t
)
=
1
b
(
t
)
=
k
1
e
−
t
2
{\displaystyle y'(t)=y(t)+{k_{1}e^{-t} \over 2}\qquad a(t)=1\qquad b(t)={k_{1}e^{-t} \over 2}}
α
(
t
)
=
∫
0
t
a
(
s
)
d
s
=
∫
0
t
1
d
s
=
t
{\displaystyle \alpha (t)=\int _{0}^{t}a(s)ds=\int _{0}^{t}1ds=t}
y
(
t
)
=
e
α
(
t
)
(
∫
0
t
e
−
α
(
t
)
⋅
b
(
s
)
d
s
)
=
e
t
(
∫
0
t
e
−
s
⋅
k
1
2
e
−
s
d
s
)
=
e
t
(
∫
0
t
k
1
2
e
−
2
s
d
s
)
=
e
t
(
−
k
1
2
⋅
e
−
2
t
2
+
c
)
=
−
k
1
4
e
−
t
+
c
⋅
e
t
{\displaystyle y(t)=e^{\alpha (t)}\left(\int _{0}^{t}e^{-\alpha (t)}\cdot b(s)ds\right)=e^{t}\left(\int _{0}^{t}e^{-s}\cdot {k_{1} \over 2}e^{-s}ds\right)=e^{t}\left(\int _{0}^{t}{k_{1} \over 2}e^{-2s}ds\right)=e^{t}\left(-{k_{1} \over 2}\cdot {e^{-2t} \over 2}+c\right)=-{k_{1} \over 4}e^{-t}+c\cdot e^{t}}
y
(
0
)
=
−
k
1
4
e
−
0
+
c
⋅
e
0
=
1
→
c
=
1
+
k
1
4
{\displaystyle y(0)=-{k_{1} \over 4}e^{-0}+c\cdot e^{0}=1\rightarrow c=1+{k_{1} \over 4}}
y
(
1
)
=
−
k
1
4
e
−
1
+
c
⋅
e
1
=
0
→
c
=
0
+
k
1
4
e
−
1
e
=
k
1
4
⋅
e
−
2
{\displaystyle y(1)=-{k_{1} \over 4}e^{-1}+c\cdot e^{1}=0\rightarrow c={0+{k_{1} \over 4}e^{-1} \over e}={k_{1} \over 4}\cdot e^{-2}}
1
+
k
1
4
=
k
1
4
⋅
e
−
2
→
4
+
k
1
=
e
−
2
k
1
→
k
1
(
1
−
e
−
2
)
=
−
4
→
k
1
=
−
4
1
−
e
−
2
≈
−
4
,
62607
{\displaystyle {1+k_{1} \over 4}={k_{1} \over 4}\cdot e^{-2}\rightarrow 4+k_{1}=e^{-2}k_{1}\rightarrow k_{1}(1-e^{-2})=-4\rightarrow k_{1}={-4 \over 1-e^{-2}}\approx -4,62607}
c
=
1
+
k
1
4
≈
1
−
4
,
62
4
≈
−
0
,
15652
{\displaystyle c=1+{k_{1} \over 4}\approx 1-{4,62 \over 4}\approx -0,15652}
Logo:
λ
∗
(
t
)
=
k
1
e
−
t
≈
−
4
,
63
e
−
t
{\displaystyle {\color {blue}\lambda ^{*}(t)}=k_{1}e^{-t}\approx \color {blue}-4,63e^{-t}}
u
∗
(
t
)
=
k
1
e
−
t
2
≈
−
2
,
31
e
−
t
{\displaystyle {\color {blue}u^{*}(t)}={k_{1}e^{-t} \over 2}\approx \color {blue}-2,31e^{-t}}
y
∗
(
t
)
=
−
k
1
4
⋅
e
−
t
+
c
⋅
e
t
≈
1
,
16
e
−
t
−
0
,
16
e
t
{\displaystyle {\color {blue}y^{*}(t)}=-{k_{1} \over 4}\cdot e^{-t}+c\cdot e^{t}\approx \color {blue}1,16e^{-t}-0,16e^{t}}
Verificar se a função Hamiltoniana é côncava em relação a
y
{\displaystyle y}
u
{\displaystyle u}
−
Hessiana
=
[
H
u
u
H
y
u
H
u
y
H
y
y
]
=
−
[
−
2
0
0
0
]
{\displaystyle -{\text{Hessiana}}={\begin{bmatrix}H_{uu}&H_{yu}\\H_{uy}&H_{yy}\end{bmatrix}}=-{\begin{bmatrix}-2&0\\0&0\end{bmatrix}}}
H
1
<
0
H
2
=
0
}
−
H
1
>
0
−
H
2
=
0
}
{\displaystyle \left.{\begin{matrix}H1<0\\H2=0\end{matrix}}\right\}\left.{\begin{matrix}-H1>0\\-H2=0\end{matrix}}\right\}}
∴
{\displaystyle \therefore }
−
H
{\displaystyle -H}
d.
max
V
=
∫
0
1
−
1
2
⋅
(
u
2
+
y
2
)
d
t
{\displaystyle V=\int _{0}^{1}-{1 \over 2}\cdot (u^{2}+y^{2})dt}
s.a
y
′
=
u
−
y
{\displaystyle y'=u-y}
y
(
0
)
=
1
{\displaystyle y(0)=1}
y
(
1
)
=
y
1
(
libre
)
{\displaystyle y(1)=y_{1}({\text{libre}})}
Construir Hamiltoniano.
H
(
t
,
λ
,
u
,
y
)
=
−
1
2
⋅
(
u
2
+
y
2
)
+
λ
⋅
(
u
−
y
)
{\displaystyle H(t,\lambda ,u,y)=-{1 \over 2}\cdot (u^{2}+y^{2})+\lambda \cdot (u-y)}
H
{\displaystyle H}
u
{\displaystyle u}
Princípio do Ótimo de Pontryagin (condição necessária de H).
∂
H
∂
u
=
−
u
+
λ
=
0
→
u
∗
=
λ
{\displaystyle {\partial H \over \partial u}=-u+\lambda =0\rightarrow u^{*}=\lambda }
As equações do movimento do problema.
y
′
=
∂
H
∂
λ
=
u
−
y
{\displaystyle y'={\partial H \over \partial \lambda }=u-y}
λ
′
=
−
∂
H
∂
y
=
y
+
λ
{\displaystyle \lambda '=-{\partial H \over \partial y}=y+\lambda }
Substituir
u
{\displaystyle u}
y
′
{\displaystyle y'}
y
′
=
u
−
y
=
λ
−
y
{\displaystyle y'=u-y=\lambda -y}
Logo,
λ
′
=
λ
+
y
y
′
=
λ
−
y
→
[
λ
y
]
′
=
[
1
1
1
−
1
]
[
λ
y
]
→
J
f
=
[
1
1
1
−
1
]
{\displaystyle {\begin{matrix}\lambda '=\lambda +y\\y'=\lambda -y\end{matrix}}\rightarrow {\begin{bmatrix}\lambda \\y\end{bmatrix}}'={\begin{bmatrix}1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}\lambda \\y\end{bmatrix}}\rightarrow J_{f}={\begin{bmatrix}1&1\\1&-1\end{bmatrix}}}
Diagrama de Fase
Encontrar as singularidades
λ
+
y
=
0
→
λ
=
−
y
{\displaystyle \lambda +y=0\rightarrow \lambda =-y}
λ
−
y
=
0
→
−
y
−
y
=
0
→
−
2
y
=
0
→
y
=
0
→
λ
=
−
y
=
0
{\displaystyle \lambda -y=0\rightarrow -y-y=0\rightarrow -2y=0\rightarrow y=0\rightarrow \lambda =-y=0}
Singularidade (0,0)
Determinar os autovalores e autovetores:
[
1
−
λ
1
1
−
1
−
λ
]
{\displaystyle {\begin{bmatrix}1-\lambda &1\\1&-1-\lambda \end{bmatrix}}}
(
1
−
λ
)
(
−
1
−
λ
)
−
1
=
0
=
−
1
−
λ
+
λ
+
λ
2
−
1
=
λ
2
−
2
→
λ
≈
±
1
,
41421
{\displaystyle (1-\lambda )(-1-\lambda )-1=0=-1{\cancel {-\lambda +\lambda }}+\lambda ^{2}-1=\lambda ^{2}-2\rightarrow \lambda \approx \pm 1,41421}
Autovetores (pelo Scilab):
v
1
=
(
−
0
,
92
−
0
,
38
)
v
2
=
(
0
,
38
−
0
,
92
)
{\displaystyle v_{1}=(-0,92\quad -0,38)\qquad v_{2}=(0,38\quad -0,92)}
e.
max
V
=
∫
0
T
−
d
t
{\displaystyle V=\int _{0}^{T}-dt}
s.a
y
′
=
y
+
u
{\displaystyle y'=y+u}
y
(
0
)
=
5
{\displaystyle y(0)=5}
y
(
T
)
=
11
(
T libre
)
{\displaystyle y(T)=11({\text{T libre}})}
Construir Hamiltoniano.
H
(
t
,
λ
,
u
,
y
)
=
−
1
+
λ
⋅
(
y
+
u
)
{\displaystyle H(t,\lambda ,u,y)=-1+\lambda \cdot (y+u)}
H
{\displaystyle H}
u
{\displaystyle u}
u
∗
(
t
)
{\displaystyle u^{*}(t)}
u
∈
[
a
,
b
]
{\displaystyle u\in [a,b]}
u
∗
(
t
)
=
a
,
se
λ
<
0
{\displaystyle u^{*}(t)=a,{\text{se }}\lambda <0}
u
∗
(
t
)
=
b
,
se
λ
>
0
{\displaystyle u^{*}(t)=b,{\text{se }}\lambda >0}
Para determinar
λ
{\displaystyle \lambda }
y
′
(
t
)
=
∂
H
∂
λ
(
t
)
=
y
(
t
)
+
u
(
t
)
{\displaystyle y'(t)={\partial H \over \partial \lambda (t)}=y(t)+u(t)}
λ
′
(
t
)
=
−
∂
H
∂
y
(
t
)
=
−
λ
(
t
)
→
integrar
λ
′
(
t
)
→
λ
(
t
)
=
k
1
e
−
t
.
{\displaystyle \lambda '(t)=-{\partial H \over \partial y(t)}=-\lambda (t)\rightarrow {\text{integrar }}\lambda '(t)\rightarrow \lambda (t)=k_{1}e^{-t}.}
e
−
t
{\displaystyle e^{-t}}
λ
{\displaystyle \lambda }
k
1
{\displaystyle k_{1}}
Como
T
{\displaystyle T}
H
(
T
)
=
0
=
−
1
+
λ
(
T
)
y
(
T
)
+
λ
(
T
)
u
(
T
)
=
−
1
+
k
1
e
−
T
⋅
11
+
k
1
e
−
T
u
(
T
)
→
u
(
T
)
=
1
k
1
e
−
T
−
11
k
1
e
−
T
k
1
e
−
T
=
e
T
k
1
−
11
{\displaystyle H(T)=0=-1+\lambda (T)y(T)+\lambda (T)u(T)=-1+k_{1}e^{-T}\cdot 11+k_{1}e^{-T}u(T)\rightarrow u(T)={1 \over k_{1}e^{-T}}-{11k_{1}e^{-T} \over k_{1}e^{-T}}={e^{T} \over k_{1}}-11}
Logo,
y
′
=
y
+
u
=
y
+
e
t
k
1
−
11
{\displaystyle y'=y+u=y+{e^{t} \over k_{1}}-11}
Porém, neste problema não foram estabelecidas as restrições para
u
{\displaystyle u}
u
∈
[
a
,
b
]
{\displaystyle u\in [a,b]}
f.
max
V
=
∫
0
∞
(
1
−
y
)
u
d
t
{\displaystyle V=\int _{0}^{\infty }(1-y)udt}
s.a
y
′
=
(
1
−
y
)
u
{\displaystyle y'=(1-y)u}
y
(
0
)
=
0
{\displaystyle y(0)=0}
u
(
t
)
∈
[
0
,
1
]
{\displaystyle u(t)\in [0,1]}
g.
max
V
=
∫
0
T
(
y
2
+
a
y
+
b
u
+
c
u
2
)
d
t
{\displaystyle V=\int _{0}^{T}(y^{2}+ay+bu+cu^{2})dt}
s.a
y
′
=
u
{\displaystyle y'=u}
y
(
0
)
=
d
{\displaystyle y(0)=d}
y
(
T
)
=
y
T
(
T libre
)
{\displaystyle y(T)=y_{T}({\text{T libre}})}
a
,
b
,
c
,
d
>
0
{\displaystyle a,b,c,d>0}
h.
max
V
=
∫
0
1
(
2
y
−
3
u
−
u
2
)
d
t
{\displaystyle V=\int _{0}^{1}(2y-3u-u^{2})dt}
s.a
y
′
=
y
+
u
{\displaystyle y'=y+u}
y
(
0
)
=
5
{\displaystyle y(0)=5}
y
(
1
)
=
y
1
(
libre
)
{\displaystyle y(1)=y_{1}({\text{libre}})}
4. La curva de demanda de un mercado en el instante "
t
{\displaystyle t}
q
(
t
)
=
a
−
b
q
(
t
)
a
,
b
>
0
{\displaystyle q(t)=a-bq(t)\qquad a,b>0}
Donde
q
(
t
)
{\displaystyle q(t)}
p
(
t
)
{\displaystyle p(t)}
p
∗
{\displaystyle p^{*}}
(
y
(
t
)
)
{\displaystyle (y(t))}
y
′
=
k
(
p
−
p
∗
)
k
>
0
{\displaystyle y'=k(p-p^{*})\qquad k>0}
y
(
0
)
=
y
0
y
0
>
0
{\displaystyle y(0)=y_{0}\qquad y_{0}>0}
La compañía grande produce una cantidad
q
(
t
)
−
y
(
t
)
{\displaystyle q(t)-y(t)}
(
p
∗
>
c
>
0
)
{\displaystyle (p^{*}>c>0)}
r
{\displaystyle r}
Π
=
∫
0
∞
e
−
n
[
p
−
c
]
[
a
−
b
p
−
y
]
d
t
{\displaystyle \Pi =\int _{0}^{\infty }e^{-n}[p-c][a-bp-y]dt}
a. Plante un diagrama de fase que explique la dinámica del precio y la producción de las pequeñas firmas.
b. Encuentre el valor del precio y la producción de las pequeñas firmas en le estado estacionario.
V
{\displaystyle V}
P
{\displaystyle P}
V
′
=
−
a
V
+
b
P
[
1
−
V
M
]
a
,
b
,
M
>
0
{\displaystyle V'=-aV+bP\left[1-{V \over M}\right]\qquad a,b,M>0}
Dado
V
(
0
)
=
V
0
V
0
>
0
{\displaystyle V(0)=V_{0}\qquad V_{0}>0}
Donde M es el valor de las ventas de todas las empresas dentro del mercado. El objetivo de la empresa es maximizar el valor de las ventas hasta el período "
T
{\displaystyle T}
I
=
∫
0
T
V
(
t
)
d
t
{\displaystyle I=\int _{0}^{T}V(t)dt}
a. Si la firma XYZ puede destinar a lo más
3
,
000
{\displaystyle 3,000}
a
=
1
,
b
=
2
,
M
=
100
,
α
=
4
,
T
=
12
{\displaystyle a=1,b=2,M=100,\alpha =4,T=12}
t
=
0
{\displaystyle t=0}
T
{\displaystyle T}
v
(
∗
)
{\displaystyle v(*)}
p
{\displaystyle p}
u
{\displaystyle u}
e
π
{\displaystyle e^{\pi }}
V
=
∫
0
T
v
(
u
,
p
)
e
π
d
t
r
>
0
{\displaystyle V=\int _{0}^{T}v(u,p)e^{\pi }dt\qquad r>0}
La inflación, el desempleo y la inflación esperada (
π
{\displaystyle \pi }
p
=
a
−
b
u
+
c
π
a
,
b
,
c
>
0
{\displaystyle p=a-bu+c\pi \qquad a,b,c>0}
Por otra parte, la inflación esperada se forma de acuerdo con expectativas adaptativas:
v
(
u
,
p
)
=
−
u
2
−
k
p
k
>
0
{\displaystyle v(u,p)=-u^{2}-kp\qquad k>0}
a. Halle la trayectoria del desempleo, la inflación y la inflación esperada, si el valor inicial de la inflación esperada es
π
(
0
)
=
π
0
{\displaystyle \pi (0)=\pi _{0}}
6.3 Comprobar que las siguientes sucesiones dadas son soluciones de las ecuaciones:
a)
x
t
=
cos
π
t
;
x
t
+
1
=
−
x
t
.
{\displaystyle {\text{a) }}x_{t}=\cos \pi t;x_{t+1}=-x_{t}.}
x
t
=
cos
(
π
⋅
t
)
→
sequência
{\displaystyle x_{t}=\cos(\pi \cdot t)\rightarrow {\text{sequência}}}
x
0
=
cos
(
π
⋅
0
)
=
cos
0
=
1
{\displaystyle x_{0}=\cos(\pi \cdot 0)=\cos 0=1}
x
1
=
cos
(
π
⋅
1
)
=
−
1
{\displaystyle x_{1}=\cos(\pi \cdot 1)=-1}
x
2
=
cos
(
π
⋅
2
)
=
1
{\displaystyle x_{2}=\cos(\pi \cdot 2)=1}
x
3
=
cos
(
π
⋅
3
)
=
−
1
{\displaystyle x_{3}=\cos(\pi \cdot 3)=-1}
x
t
→
sequência
{
1
,
−
1
,
1
,
−
1
,
1
,
−
1
,
⋯
}
{\displaystyle x_{t}\rightarrow {\text{sequência }}\{1,-1,1,-1,1,-1,\cdots \}}
cos
π
t
{
1
,
se
t
é par
−
1
,
se
t
é ímpar
}
x
t
=
(
−
1
)
t
{\displaystyle \cos \pi t\left\{{\begin{matrix}1,{\text{ se }}t{\text{ é par}}\\-1,{\text{ se }}t{\text{ é ímpar}}\end{matrix}}\right\}x_{t}=(-1)^{t}}
Portanto,
x
t
+
1
=
cos
(
π
⋅
(
t
+
1
)
)
=
(
−
1
)
⋅
cos
(
π
⋅
t
)
=
−
x
t
{\displaystyle x_{t+1}=\cos(\pi \cdot (t+1))=(-1)\cdot \cos(\pi \cdot t)=-x_{t}}
x
t
+
1
=
−
x
t
{\displaystyle x_{t+1}=-x_{t}}
b)
x
t
=
2
t
;
x
t
+
1
=
x
t
+
2
x
t
−
1
.
{\displaystyle {\text{b) }}x_{t}=2^{t};x_{t+1}=x_{t}+2x_{t-1}.}
x
t
=
2
t
→
sequência
{\displaystyle x_{t}=2^{t}\rightarrow {\text{sequência}}}
x
0
=
2
0
=
1
{\displaystyle x_{0}=2^{0}=1}
x
1
=
2
1
=
2
{\displaystyle x_{1}=2^{1}=2}
x
2
=
2
2
=
4
{\displaystyle x_{2}=2^{2}=4}
x
3
=
2
3
=
8
{\displaystyle x_{3}=2^{3}=8}
x
t
→
sequência
{
1
,
2
,
4
,
8
,
⋯
}
{\displaystyle x_{t}\rightarrow {\text{sequência }}\{1,2,4,8,\cdots \}}
Como
x
t
=
2
t
{\displaystyle x_{t}=2^{t}}
x
t
+
1
=
2
t
+
1
=
2
t
⋅
2
1
=
2
(
2
t
)
=
2
t
+
2
t
=
2
t
+
2
1
+
t
−
1
=
2
t
+
2
(
2
t
−
1
)
{\displaystyle x_{t+1}=2^{t+1}=2^{t}\cdot 2^{1}=2(2^{t})=2^{t}+2^{t}=2^{t}+2^{1+t-1}=2^{t}+2(2^{t-1})}
2
t
{\displaystyle 2^{t}}
x
t
{\displaystyle x_{t}}
2
t
−
1
{\displaystyle 2^{t-1}}
x
t
−
1
{\displaystyle x_{t-1}}
x
t
+
2
x
t
−
1
{\displaystyle x_{t}+2x_{t-1}}
x
t
+
1
=
x
t
+
2
x
t
−
1
{\displaystyle x_{t+1}=x_{t}+2x_{t-1}}
c)
x
t
=
t
(
t
+
1
)
2
;
x
t
+
1
=
x
t
+
t
+
1.
{\displaystyle {\text{c) }}x_{t}={t(t+1) \over 2};x_{t+1}=x_{t}+t+1.}
Como
x
t
=
t
(
t
+
1
)
2
{\displaystyle x_{t}={t(t+1) \over 2}}
x
t
+
1
=
(
t
+
1
)
(
(
t
+
1
)
+
1
)
2
=
(
t
+
1
)
(
t
+
2
)
2
=
t
2
+
t
+
2
t
+
2
2
=
t
2
+
t
2
+
2
t
2
+
2
2
=
t
(
t
+
1
)
2
+
t
+
1
{\displaystyle x_{t+1}={(t+1)((t+1)+1) \over 2}={(t+1)(t+2) \over 2}={t^{2}+t+2t+2 \over 2}={t^{2}+t \over 2}+{2t \over 2}+{2 \over 2}={t(t+1) \over 2}+t+1}
Substituindo
t
(
t
+
1
)
2
{\displaystyle {t(t+1) \over 2}}
x
t
{\displaystyle x_{t}}
x
t
+
1
=
x
t
+
t
+
1
{\displaystyle x_{t+1}=x_{t}+t+1}
x
t
{\displaystyle x_{t}}
Apenas para lembrete:
{
x
t
=
a
t
⋅
x
0
,
se
b
=
0
x
t
=
b
1
−
a
+
a
t
⋅
(
x
0
−
b
1
−
a
)
,
se
b
≠
0
e
a
≠
1
{\displaystyle \left\{{\begin{matrix}x_{t}=a^{t}\cdot x_{0},{\text{ se }}b=0\\x_{t}={b \over 1-a}+a^{t}\cdot \left(x_{0}-{b \over 1-a}\right),{\text{ se }}b\neq 0{\text{ e }}a\neq 1\end{matrix}}\right.}
a)
x
t
+
1
=
−
0.5
x
t
+
3
{\displaystyle {\text{a) }}x_{t+1}=-0.5x_{t}+3}
Como
(
a
≠
1
e
b
≠
0
)
{\displaystyle (a\neq 1{\text{ e }}b\neq 0)}
x
t
=
b
1
−
a
+
a
t
⋅
(
x
0
−
b
1
−
a
)
=
3
1
−
(
−
0
,
5
)
+
(
−
0
,
5
)
t
⋅
(
x
0
−
3
1
−
(
−
0
,
5
)
)
=
3
3
2
+
(
−
0
,
5
)
t
⋅
(
x
0
−
3
3
2
)
=
2
+
(
−
0
,
5
)
t
⋅
(
x
0
−
2
)
{\displaystyle x_{t}={b \over 1-a}+a^{t}\cdot \left(x_{0}-{b \over 1-a}\right)={3 \over 1-(-0,5)}+(-0,5)^{t}\cdot \left(x_{0}-{3 \over 1-(-0,5)}\right)={3 \over {3 \over 2}}+(-0,5)^{t}\cdot \left(x_{0}-{3 \over {3 \over 2}}\right)=2+(-0,5)^{t}\cdot (x_{0}-2)}
Como
(
−
0
,
5
)
t
{\displaystyle (-0,5)^{t}}
t
→
∞
{\displaystyle t\to \infty }
(
−
0
,
5
)
t
⋅
(
x
0
−
2
)
{\displaystyle (-0,5)^{t}\cdot (x_{0}-2)}
∴
{\displaystyle \therefore }
lim
t
→
∞
2
+
(
−
0
,
5
)
t
⋅
(
x
0
−
2
)
=
2.
{\displaystyle \lim _{t\to \infty }2+(-0,5)^{t}\cdot (x_{0}-2)=2.}
2
{\displaystyle 2}
b)
2
x
t
+
1
=
3
x
t
+
4
{\displaystyle {\text{b) }}2x_{t+1}=3x_{t}+4}
x
t
+
1
=
3
x
t
+
4
2
=
3
2
⋅
x
t
+
2
{\displaystyle x_{t+1}={3x_{t}+4 \over 2}={3 \over 2}\cdot x_{t}+2}
Como
(
a
≠
1
e
b
≠
0
)
{\displaystyle (a\neq 1{\text{ e }}b\neq 0)}
x
t
=
b
1
−
a
+
a
t
⋅
(
x
0
−
b
1
−
a
)
=
2
1
−
3
2
+
(
3
2
)
t
⋅
(
x
0
−
2
1
−
3
2
)
=
−
4
+
1
,
5
t
⋅
(
x
0
+
4
)
{\displaystyle x_{t}={b \over 1-a}+a^{t}\cdot \left(x_{0}-{b \over 1-a}\right)={2 \over 1-{3 \over 2}}+\left({3 \over 2}\right)^{t}\cdot \left(x_{0}-{2 \over 1-{3 \over 2}}\right)=-4+1,5^{t}\cdot (x_{0}+4)}
1
,
5
t
⋅
(
x
0
+
4
)
{\displaystyle 1,5^{t}\cdot (x_{0}+4)}
t
→
∞
{\displaystyle t\to \infty }
∴
{\displaystyle \therefore }
lim
t
→
∞
−
4
+
1
,
5
t
⋅
(
x
0
+
4
)
=
∞
.
{\displaystyle \lim _{t\to \infty }-4+1,5^{t}\cdot (x_{0}+4)=\infty .}
c)
x
t
+
1
=
−
x
t
+
5
{\displaystyle {\text{c) }}x_{t+1}=-x_{t}+5}
Como
(
a
≠
1
e
b
≠
0
)
{\displaystyle (a\neq 1{\text{ e }}b\neq 0)}
x
t
=
b
1
−
a
+
a
t
⋅
(
x
0
−
b
1
−
a
)
=
5
1
−
(
−
1
)
+
(
−
1
)
t
⋅
(
x
0
−
5
1
−
(
−
1
)
)
=
5
2
+
(
−
1
)
t
⋅
(
x
0
−
5
2
)
{\displaystyle x_{t}={b \over 1-a}+a^{t}\cdot \left(x_{0}-{b \over 1-a}\right)={5 \over 1-(-1)}+(-1)^{t}\cdot \left(x_{0}-{5 \over 1-(-1)}\right)={5 \over 2}+(-1)^{t}\cdot \left(x_{0}-{5 \over 2}\right)}
(
−
1
)
t
{
1
,
se
t
é par
−
1
,
se
t
é ímpar
{\displaystyle (-1)^{t}\left\{{\begin{matrix}1,{\text{ se }}t{\text{ é par}}\\-1,{\text{ se }}t{\text{ é ímpar}}\end{matrix}}\right.}
∴
{\displaystyle \therefore }
lim
t
→
∞
5
2
+
(
−
1
)
t
⋅
(
x
0
−
5
2
)
{\displaystyle \lim _{t\to \infty }{5 \over 2}+(-1)^{t}\cdot \left(x_{0}-{5 \over 2}\right)}
d)
x
t
+
1
−
x
t
=
−
4
3
x
t
{\displaystyle {\text{d) }}x_{t+1}-x_{t}=-{4 \over 3}x_{t}}
x
t
+
1
=
−
4
3
x
t
+
x
t
=
−
2
3
x
t
{\displaystyle x_{t+1}=-{4 \over 3}x_{t}+x_{t}=-{2 \over 3}x_{t}}
Como
(
b
=
0
)
{\displaystyle (b=0)}
x
t
=
a
t
⋅
x
0
=
(
−
1
3
)
t
⋅
x
0
{\displaystyle x_{t}=a^{t}\cdot x_{0}=\left(-{1 \over 3}\right)^{t}\cdot x_{0}}
Como
(
−
1
3
)
t
{\displaystyle \left(-{1 \over 3}\right)^{t}}
t
→
∞
{\displaystyle t\to \infty }
lim
t
→
∞
(
−
1
3
)
t
⋅
x
0
=
0.
{\displaystyle \lim _{t\to \infty }\left(-{1 \over 3}\right)^{t}\cdot x_{0}=0.}
Y
t
{\displaystyle Y_{t}}
Y
t
+
1
=
C
t
+
I
t
,
{\displaystyle Y_{t+1}=C_{t}+I_{t},}
en donde
I
t
{\displaystyle I_{t}}
C
t
{\displaystyle C_{t}}
C
t
=
m
Y
t
+
c
{\displaystyle C_{t}=mY_{t}+c}
m
<
1
{\displaystyle m<1}
c
>
0
{\displaystyle c>0}
I
t
=
I
{\displaystyle I_{t}=I}
Consumo
C
t
=
m
Y
t
+
c
m
<
1
c
>
0
I
t
=
I
(investimento constante)
{\displaystyle {\text{Consumo }}C_{t}=mY_{t}+c\qquad m<1\qquad c>0\qquad I_{t}=I{\text{ (investimento constante)}}}
Y
t
+
1
=
C
t
+
I
t
=
m
Y
t
+
c
+
I
(
a
=
m
≠
1
por ser menor que
1
,
b
=
c
+
I
≠
0
)
{\displaystyle Y_{t+1}=C_{t}+I_{t}=mY_{t}+c+I\qquad (a=m\neq 1{\text{ por ser menor que }}1,b=c+I\neq 0)}
Y
t
=
b
1
−
a
+
a
t
⋅
(
x
0
−
b
1
−
a
)
=
c
+
I
1
−
m
+
m
t
⋅
(
Y
0
−
c
+
I
1
−
m
)
.
{\displaystyle Y_{t}={b \over 1-a}+a^{t}\cdot \left(x_{0}-{b \over 1-a}\right)={c+I \over 1-m}+m^{t}\cdot \left(Y_{0}-{c+I \over 1-m}\right).}
Y
∗
=
c
+
I
1
−
m
.
{\displaystyle Y^{*}={c+I \over 1-m}.}
lim
t
→
∞
Y
t
=
lim
t
→
∞
Y
∗
+
m
t
⋅
(
Y
0
−
Y
∗
)
{\displaystyle \lim _{t\to \infty }Y_{t}=\lim _{t\to \infty }Y^{*}+m^{t}\cdot (Y_{0}-Y^{*})}
Y
∗
>
0
{\displaystyle Y^{*}>0}
c
{\displaystyle c}
I
{\displaystyle I}
m
{\displaystyle m}
1
{\displaystyle 1}
Se
m
∈
(
−
1
,
1
)
∖
0
{\displaystyle m\in (-1,1)\setminus 0}
lim
t
→
∞
Y
∗
+
m
t
⋅
(
Y
0
−
Y
∗
)
=
Y
∗
{\displaystyle \lim _{t\to \infty }Y^{*}+m^{t}\cdot (Y_{0}-Y^{*})=Y^{*}}
m
>
0
{\displaystyle m>0}
m
<
0
{\displaystyle m<0}
Conforme as condições iniciais, o
m
{\displaystyle m}
1
{\displaystyle 1}
m
<
−
1
{\displaystyle m<-1}
lim
t
→
∞
Y
∗
+
m
t
⋅
(
Y
0
−
Y
∗
)
{\displaystyle \lim _{t\to \infty }Y^{*}+m^{t}\cdot (Y_{0}-Y^{*})}
↑ CROUZEIX, Jean Pierre; KERAGHEL, Abdelkrim; SANDOVAL, Wilfredo Sosa. Programación Matemática Diferenciable . Lima: Universidad Nacional de Ingeniería - Faculdad de Ciencias, 2011.
↑ LOMELÍ, Héctor y RUMBOS, Beatriz. Métodos Dinámicos en Economía. Outra Búsqueda del Tiempo Perdido . Río Hondo: Instituto Tecnológico Autónomo de México, 2001.
↑ BONIFAZ F., José Luis; LAMA C., Ruy. Optimización dinámica y teoría económica . Lima: Centro de Investigatión de la Universidad del Pacífico, 1999.
↑ BONIFAZ F., José Luis; LAMA C., Ruy. Optimización dinámica y teoría económica . Lima: Centro de Investigatión de la Universidad del Pacífico, 1999.
↑ LOMELÍ, Héctor y RUMBOS, Beatriz. Métodos Dinámicos en Economía. Outra Búsqueda del Tiempo Perdido . Río Hondo: Instituto Tecnológico Autónomo de México, 2001.
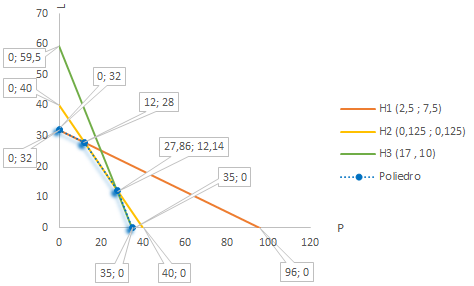
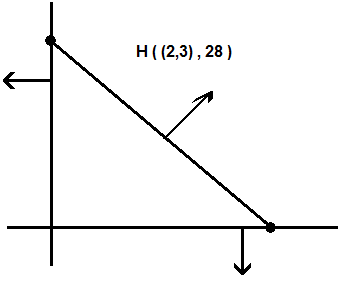



















![{\displaystyle [2{,}5;7{,}5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/567cf40a3072f9e19f2b0bc2f051a151b03e3fa8)

![{\displaystyle [0{,}125;0{,}125]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/075cadc4f3633c14bb24720dbc077aa5afd7bb13)

![{\displaystyle [17,10]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae77e5c4fa319de608ca5835467b622575f4a3ff)



![{\displaystyle x=[96;0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/345b1d4cf45f8f9c0b0e02961cec68363275c606)
![{\displaystyle y=[0;32]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/463b5b923178fbc463574fece1f66877d50f2d60)














![{\displaystyle A=[2.5\quad 7.5\quad ;\quad 0.125\quad 0.125]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/815eda77be1a0d78b78b4f28beb10e3bd5dcb0a2)
![{\displaystyle b=[240\quad ;\quad 5]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a379c94ddab0319541af918be1521356296c9272)


![{\displaystyle x1=[12\quad 28]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b4d7a3ffd48c89845770aa74f1ea06ef9300aab)
![{\displaystyle A=[2.5\quad 7.5\quad ;\quad -1\quad 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abdf5e00cc85c50d3da56f15788f970de5d45db0)

![{\displaystyle B=A'=A^{T}=[2.5\quad -1\quad ;\quad 7.5\quad 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c40f1c8087ff8e86d95a52697d8242492137749)
![{\displaystyle c=[180\quad ;\quad 120]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7e1cdb9782bff1da32549947770f4faf96949bc)

![{\displaystyle [16\quad -140]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4df26c93405762bbb1e7462d688af6213516b913)
![{\displaystyle [-12\quad 1680]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aaa27996782d2f4a955eaded28f35c20d9648feb)
![{\displaystyle {\color {Blue}[274{,}28571\quad 8{,}5714286]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7b6de7e1d6e0d1de1cee65037e429715b924d299)
![{\displaystyle [10{,}588235\quad -14{,}117647]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a5f13b3b59cef7ccc4cbc47f4c74e6332f06b99)







































































![{\displaystyle {d \over dt}\left[{\partial L \over \partial x'(t)}(t,x(t),x'(t))\right]=-2x''(t)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f68e96fc31cd1932ad1e5cead6feed0991332cb3)
![{\displaystyle {\partial L \over \partial x(t)}(t,x(t),x'(t))-{d \over dt}\left[{\partial L \over \partial x'(t)}(t,x(t),x'(t))\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb98e07d02a4ace409c9023bdcd6a0a48e309f7e)



























![{\displaystyle {d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=x''\cdot (1+(x')^{2})^{-{1 \over 2}}-{1 \over 2}\cdot x'\cdot (1+(x')^{2})^{-{3 \over 2}}\cdot (0+2\cdot x'\cdot x'')=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d965d2078d266e64c3a123056a81bd51b00b9682)


![{\displaystyle {\partial L \over \partial x}(t,x,x')-{d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c7354da3ed6191f56f7603f5c587341b472d92b7)











![{\displaystyle {d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=2x''}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64aca8b9ef1d6898e35bc40e65a92e0876e0a8f0)











![{\displaystyle {d \over dt}\left[{\partial L \over \partial x'}(t,x,x')\right]=1+2x''}](https://wikimedia.org/api/rest_v1/media/math/render/svg/97010f43e8b291cd642a2ae67939886d2635a29d)






![{\displaystyle {\text{P5 (a): }}J[x]=\int _{0}^{40}-{{\dot {x}}^{2} \over 2}dt\quad {\text{con}}\quad x(0)=20\quad {\text{y}}\quad x(40)=0{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/207ecca612f4cf937e24d29e9203440145248443)



![{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=-{\ddot {x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e8afa54b70fd7100db6b57a5b61454cf0dc36b03)
![{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cd5d6aa97674eca9cb8b2c18cd770c0de5faf25)











![{\displaystyle {\text{P5 (b): }}J[x]=\int _{0}^{10}-(2x{\dot {x}}+{\dot {x}}^{2})dt\quad {\text{con}}\quad x(0)=10\quad {\text{y}}\quad x(10)=100{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9e07a918c77f62cd76d58a92b4e5b770c7c61e81)



![{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=-2{\dot {x}}-2{\ddot {x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/48348e0fbfe87e5f03fcbffe72c997e2cd0ae155)








![{\displaystyle {\text{P5 (c): }}J[x]=\int _{0}^{2}(12tx+{\dot {x}}^{2})dt\quad {\text{con}}\quad x(0)=1\quad {\text{y}}\quad x(2)=17{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a6bebef40d8329e419e8d9a17cd2e1a3aaf1b39c)



![{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=2{\ddot {x}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f4f788a647825fe5b0dafb2b1c237e213010219f)








![{\displaystyle {\text{P5 (d): }}J[x]=\int _{0}^{2}(x+{\dot {x}}^{2})dt\quad {\text{con}}\quad x(0)=1\quad {\text{y}}\quad x(2)=10{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b0083b7ef0af474a7273e2ea3cd9b5fe6fc91b)








![{\displaystyle {\text{P5 (e): }}J[x]=\int _{0}^{2}(x^{2}+t^{2}{\dot {x}})dt\quad {\text{con}}\quad x(0)=0\quad {\text{y}}\quad x(2)=2{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68199a2059bbf52a88f0dfb8ccc799ad87551248)



![{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}})\right]=2t}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9f26b2973e04c2cfa706baee4b5fe9817f693557)



![{\displaystyle {\text{P5 (f): }}J[x,y]=\int _{0}^{T}(2xy-2x^{2}-{\dot {x}}^{2}+{\dot {y}}^{2})dt\quad {\text{encontrar únicamente la solución general.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c34d2de2ac6f0bf467fae2b2cd125c9eb6659f4d)



![{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {z}}}\right]={\begin{bmatrix}-2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4545ac43174c06536f73d4dfa298753dfdc94ed)
![{\displaystyle {\partial L \over \partial z}(t,x,{\dot {x}},y,{\dot {y}})-{d \over dt}\left[{\partial L \over \partial {\dot {z}}}(t,x,{\dot {x}},y,{\dot {y}})\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/194b84c03ef73af84adbc83c4678a5ee992e3b2d)












![{\displaystyle {\text{P5 (g): }}J[x,y]=\int _{0}^{10}({\dot {x}}^{2}+{\dot {y}}^{2}+e^{t})dt\quad {\text{dadas}}\quad x(0)=0\quad {\text{,}}\quad y(0)=2\quad {\text{,}}\quad x(10)=11\quad {\text{y}}\quad y(10)=6{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/808631ee46212fdee2839b9288631d84d60c9ee3)



![{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {z}}}\right]={\begin{bmatrix}2{\ddot {x}}\\2{\ddot {y}}\end{bmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1197cfdb4b3cd9e63e32d434d23dc7d42e85f8d5)









![{\displaystyle {\text{P5 (h): }}J[x,y]=\int _{0}^{\pi \over 2}({\dot {x}}^{2}+{\dot {y}}^{2}+2xy)dt\quad {\text{dadas}}\quad x(0)=y(0)=0\quad {\text{y}}\quad x\left({\pi \over 2}\right)=y\left({\pi \over 2}\right)=1{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2a2b711cf8e5f1f7aaef775bce9854d418785ba9)









![{\displaystyle {\text{P5 (i): }}J[x]=\int _{0}^{1}(1+{\ddot {x}}^{2})dt\quad {\text{con}}\quad x(0)=0\quad {\text{y}}\quad {\dot {x}}(0)=x(1)={\dot {x}}(1)=1{\text{.}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5622321c7fc1ebfffe6b184bc44345be70e189df)



![{\displaystyle {d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aa094c5688ce180e09897a7a1e2795d801443e25)

![{\displaystyle {d^{2} \over dt^{2}}\left[{\partial L \over \partial {\ddot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]=2{\dot {\ddot {x}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/44bdfb4100aae3aef928bf5079d54ba618f97bfe)
![{\displaystyle {\partial L \over \partial x}(t,x,{\dot {x}},{\ddot {x}})-{d \over dt}\left[{\partial L \over \partial {\dot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]+{d^{2} \over dt^{2}}\left[{\partial L \over \partial {\ddot {x}}}(t,x,{\dot {x}},{\ddot {x}})\right]=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a1533f4ba4afbce0b219cfd2a1938b077158a68a)










































































































![{\displaystyle u\in [a,b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a3e30d854d2eecf93ed403ee32d94b7306cc2b6c)


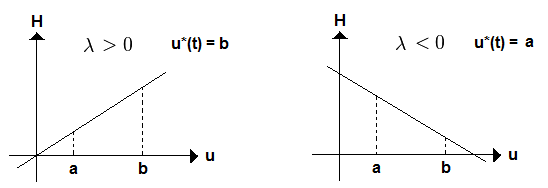









![{\displaystyle u(t)\in [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ca630a00ece8ac9b61c9f7e0146c8c95a8386b01)















![{\displaystyle \Pi =\int _{0}^{\infty }e^{-n}[p-c][a-bp-y]dt}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abbae6e4ddb05f0c8aca88c8d07b13d58f878394)

![{\displaystyle V'=-aV+bP\left[1-{V \over M}\right]\qquad a,b,M>0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c63725a79ddd5ba9bdf357c8ed13ab33474191a9)