Discussão:Introdução à física/Mecânica
Aspeto
O texto abaixo foi retirado do livro de Física, porém inclui integrais, o que o torna inapropriado para o livro de Física de nível médio, porém pode ser aproveitado em um livro universitário de Mecânica.
Este movimento tem aceleração constante, e é fácil imaginar como ficaria um gráfico da aceleração (a) versus tempo (t). Agora, a aceleração é a taxa de váriação da velocidade no tempo, logo, integrando a área (A) da figura formada pela reta a(t) e o eixo das abcissas (um retângulo) podemos chegar a uma relação para calcular a velocidade istantânea da partícula:
Logo,
Integrando novamente:
Sabemos das relações de movimento uniforme que 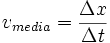 e é fácil notar que
e é fácil notar que 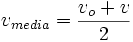 , sabemos também, pelas equação desta seção que
, sabemos também, pelas equação desta seção que 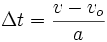 então juntando tudo temos que
então juntando tudo temos que
O histórico anterior da página foi arquivado para fins de backup em Discussão:Introdução à física/Mecânica/Arquivo LQT 1 em 2015-11-03.