Algoritmos e Estruturas de Dados/Árvores Binárias

Árvore binária é uma estrutura de dados caracterizada por:

Ou não tem elemento algum (árvore vazia).
Ou tem um elemento distinto, denominado raiz, com dois apontamentos para duas estruturas diferentes, denominadas sub-árvore esquerda e sub-árvore direita.

Perceba que a definição é recursiva e, devido a isso, muitas operações sobre árvores binárias utilizam recursão. É o tipo de árvore mais utilizado na computação. A principal utilização de árvores binárias são as árvores de busca.

Implementação de um Nó de uma árvore binária em C++

Como definimos anteriormente, um nó de uma árvore binária é composto por, pelo menos, três elementos, a sua chave e mais dois ponteiros que apontarão um para a sub-árvore esquerda e outro para a sub-árvore direita. em C nós poderíamos criar uma estrutura do tipo Struct para representar esse nó, mas em C++ podemos criar uma classe de forma que possamos manipular os nós mais facilmente através dos métodos sets e gets da classe.

class No 
{
private:
    /* Aqui vão as informações do nó, no nosso caso usaremos apenas um inteiro como chave,
    mas poderíamos usar qualquer outra informação junto com as chaves como strings, boleanos etc... */
    int chave;    
    // Ponteiros do tipo Nó para as sub-arvores direitas e esquerdas respectivamentes
    No *esq;
    No *dir;
    
public:
    /*  Aqui criaremos um construtor para o nó que seta o valor da chave e inicializa os ponteiros
        das sub-arvores como null. OBS: Note que usarei nullptr em vez de NULL, se não utilizar o c++11 essa keyword 
        não funcionará. */
    No ( int chave )
    {
        this->chave = chave;    // seta a chave
        esq = nullptr;          // inicializa a sub-arvore esquerda como null.
        dir = nullptr;          // inicializa a sub-arvore direita como null.
    }
    
    // METODOS GETS E SETTERS.
    int getChave()
    {
        return chave;    
    }
    
    No* getEsq()
    {
        return esq;
    }
    
    No* getDir()
    {
        return dir;
    }
    
    void setEsq( No* esq )
    {
        this->esq = esq;
    }
    
    void setDir( No* dir )
    {
        this->dir = dir;
    }
};

Definições para árvores binárias

Os nós de uma árvore binária possuem graus zero, um ou dois. Um nó de grau zero é denominado folha.

Uma árvore binária é considerada estritamente binária se cada nó da árvore possui grau zero ou dois.

A profundidade de um nó é a distância deste nó até a raiz. Um conjunto de nós com a mesma profundidade é denominado nível da árvore. Denominamos altura, a maior profundidade existente na árvore, ou seja, a profundidade do nó mais profundo.

Uma árvore é dita completa se todas as folhas da árvore estão no mesmo nível da árvore.

Definições em teoria dos grafos

Em teoria dos grafos, uma árvore binária é definida como um grafo acíclico, conexo, dirigido e que cada nó não tem grau maior que 2. Assim sendo, só existe um caminho entre dois nós distintos.

E cada ramo da árvore é um vértice dirigido, sem peso, que parte do pai e vai o filho.

Percursos em árvore

Existem três tipos de percursos: Percurso em InOrdem, PreOrdem e PosOrdem.

InOrdem

O algoritmo desse percurso é:

emOrdem(Struct No *n){
 if(n!=null){
   emOrdem(n->esq);
   visita(n);
   emOrdem(n->dir);
 }
}

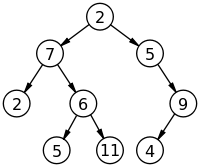
Para a árvore acima, o percurso seria: 2, 7, 5, 6, 11, 2, 5, 4 e 9.

PreOrdem

O algoritmo desse percurso é:

preOrdem(Struct No *n){
  if(n!=null){
    visita(n);
    preOrdem(n->esq);
    preOrdem(n->dir);
  }
}

Para a árvore acima, o percurso seria: 2, 7, 2, 6, 5, 11, 5, 9 e 4.

PosOrdem

O algoritmo desse percurso é:

posOrdem(Struct No *n){
 if(n!=null){
   posOrdem(n->esq);
   posOrdem(n->dir);
   visita(n);
 }
}

Para a árvore acima, o percurso seria: 2, 5, 11, 6, 7, 4, 9, 5 e 2.

Transformação de uma árvore n-ária

Uma árvore n-ária qualquer (árvore cujos nós possuem graus menores ou iguais a n) podem ser representados por uma árvore binária. Um exemplo dessa transformação pode ser vista em [1]

Métodos para representação de árvores binárias

Uma das maneiras mais simples de representar árvores binárias em linguagens de programação é por meio de arranjos unidimensionais (vetores). Dado um nó de índice i qualquer, os seus filhos terão índices 2i + 1 e 2i + 2 e o seu pai terá índice piso((i - 1)/2). Essa implementação é utilizada para representar árvores completas ou quase completas. Heaps, que são árvores binárias quase completas são implementadas na forma de um vetor de uma maneira bastante eficiente.

Apesar da simplicidade, essa representação requer uma grande quantidade de memória contígua para o armazenamento de árvores grandes, o crescimento desta é difícil de implementar e manter e pode haver grande quantidade de desperdício de memória.

Em uma linguagem que possua suporte a estruturas e referências (por exemplo Pascal e C), as árvores são implementadas a partir de nós, com um, ou mais, campos para a(s) informação(ões) principal(is) e dois campos apontadores especiais, denominados esquerda e direita, que fazem referência às sub-árvores esquerda e direita, respectivamente. Algumas vezes, há um apontador para o pai. Em um nó do tipo folha, os campos apontadores possuem valores especiais (nil em Pascal e NULL em C).