Processamento de Dados Massivos/Projeto e implementação de aplicações Big Data/Identificação de ciclos em grafos
Introdução
[editar | editar código-fonte]Detecção de Ciclos por Busca em Profundidade
[editar | editar código-fonte]Um método eficiente para detectar ciclos em grafos direcionados é por meio do algoritmo de busca em profundidade. Intuitivamente, o algoritmo começa num nó raiz (selecionando algum nó como sendo o raiz, no caso de um grafo) e explora tanto quanto possível cada um dos seus ramos, antes de retroceder [1][2].
Formalmente, um algoritmo de busca em profundidade realiza uma busca não-informada que progride através da expansão do primeiro nó filho da árvore de busca, e se aprofunda cada vez mais, até que o alvo da busca seja encontrado ou até que ele se depare com um nó que não possui filhos (nó folha). Então a busca retrocede e começa no próximo nó. Numa implementação não-recursiva, todos os nós expandidos recentemente são adicionados a uma pilha, para realizar a exploração[1].
Pseudo-Código
[editar | editar código-fonte]Entrada: Um grafo G e um vértice v de G
1 procedimento DFS(G,v): 2 marcar v como explorada 3 para cada aresta e em G.arestasAdjacentes(v) fazer 4 se aresta e estiver não-explorada então 5 w ← G.vérticeAdjacente(v,e) 6 se vértice w estiver não-explorado então 7 marcar e como uma aresta de avanço 8 chamar recursivamente DFS(G,w) 9 senão 10 marcar e como aresta de retorno 11 todo o caminho de w até v representa um ciclo
A seguir é apresentado um exemplo da execução do algoritmo de busca em profundidade. A aresta (4,2), na cor verde, representa uma aresta de retorno, e o caminho (2,3,4) representa um ciclo do grafo.

Análise do Algoritmo
[editar | editar código-fonte]A ordem de complexidade em relação ao custo de tempo de execução do algoritmo de detecção de ciclos por busca em profundidade é Θ(|V| + |E|), onde |V| é o número de vértices do grafo e |E| o número de arestas[2]. O custo de armazenamento (espaço em memória) do algoritmo é Θ(|V|).
Detecção de Ciclos no Contexto de Dados Massivos
[editar | editar código-fonte]No contexto de dados massivos, a estrutura do grafo pode ser grande o suficiente para saturar facilmente o poder de processamento ou a capacidade de memória de uma única máquina, surgindo a necessidade de paralelizar o algoritmo de detecção de ciclos. Entretanto, principalmente devido à sua característica recursiva, uma desvantagem do algoritmo de busca em profundidade é o fato de ser dificilmente paralelizável, embora o algoritmo seja assintoticamente ótimo.
Portanto, é necessário um algoritmo que divida o problema de detecção de ciclos em subproblemas entre nós de computação, de modo que os nós busquem por cíclos de maneira paralela, garantindo que todos os ciclos serão encontrados. Propõe-se então, um algoritmo para detecção de ciclos de grafo por passagem de mensagens[3] entre os vértices, baseado no modelo Pregel[4] de processamento de grafos da Google. Esse modelo apresenta uma abordagem centrada nos vértices em que os vértices do grafo trabalham juntos para detectar ciclos.
Algoritmo de Detecção de Ciclos por Passagem de Mensagens
[editar | editar código-fonte]O modelo do Pregel consiste basicamente em uma sequência de iterações, em cada uma das quais um vértice recebe mensagens enviadas por outros vértices na iteração anterior e enviar mensagens para outros vértices.
O método inicia com cada vértice enviando para seus vizinhos uma mensagem com uma lista contendo apenas o próprio vértice. Os passos seguintes consistem de pequenas computações realizadas sobre as listas recebidas por mensagens de outros vértices. Se o vértice não recebeu mensagem alguma, então o vértice se desativa. O algoritmo termina quando todos os vértices estão inativos.
Para cada lista recebida, se o vértice receber uma lista contendo a si próprio em qualquer posição exceto a primeira, o vértice rejeita a mensagem. Se a lista recebida começar com o próprio vértice, então um ciclo foi detectado. Para as demais listas recebidas, o vértice se adiciona ao final da lista e a encaminha para todos os seus vizinhos.
Por definição, temos que e vérta lista dices, que pode ser vista como uma sequência ordenada de vértices, representa um caminho no grafo[5]. Portanto, quando um vértice recebe uma lista em que o primeiro elemento da lista é o próprio vértice, temos que o caminho representado por aquela lista teve início no próprio vértice, isto é, a lista representa um ciclo no grafo.
A seguir é apresentado um exemplo da execução do algoritmo de detecção de ciclos por passagem de mensagens. Pode-se observar que no passo (d), o vértice 2 recebe uma mensagem em que a lista de vértices é iniciada pelo próprio vértice 2, detectando assim um ciclo no grafo (2,3,4). No passo (e), o vértice 2 rejeita uma mensagem contendo a si próprio na segunda posição da lista. Pode-se notar que a lista rejeitada contém o ciclo detectado anteriormente, e é por esse motivo que o vértice 2 aparece no meio da lista rejeitada, pois o ciclo é um sub-caminho do caminho representado pela lista rejeitada no passo (e). Por fim, no passo (f) todos os vértices são desativados e não existem mais mensagens sendo enviadas pelo grafo, terminando a execução do algoritmo.
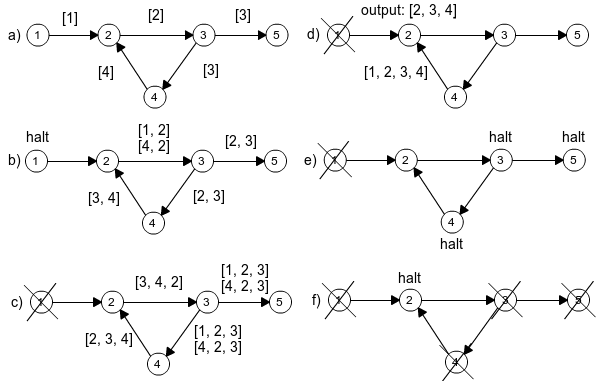
No passo (d) do exemplo, todos os três vértices detectam o ciclo (2,3,4). Para assegurar que apenas um dos vértices reportem a detecção, pode-se detectar o ciclo apenas do vértice cujo identificador seja o menor (por algum critério de ordenação) dentre os demais vértices do ciclo, onde no exemplo seria o vértice 2.
Análise do Algoritmo
[editar | editar código-fonte]O número total de iterações do algoritmo paralelo será igual ao tamanho do maior caminho de vértices distintos do grafo mais algumas poucas iterações iniciais ou finais. Portanto o número de iterações do algoritmo paralelo será Θ(|V|), sendo que o maior caminho distinto possível de um grafo seria contendo todos os vértices do grafo[3].
Pseudo-Código no Modelo Pregel de Programação Paralela
[editar | editar código-fonte]Como mencionado anteriormente, o algoritmo proposto é baseado no modelo Pregel da Google. Nesse modelo de programação paralela, os programas de usuário são expressos como sequências de iterações, chamadas de supersteps, nas quais cada vértice recebe mensagens enviadas por outros vértices na iteração anterior, envia mensagens para outros vértices, e modifica seu próprio estado e o estado das arestas de saída. O modelo Pregel é projetado para implementações em clusters de computadores que sejam eficientes, escaláveis e tolerante a falhas, de maneira que detalhes referentes à distribuição são escondidos pela abstração da API.
O usuário desse modelo implementa um método chamado COMPUTE, que será executado por todos os vértices ativos em cada superstep. O vértice se desativa votando para parar (halt) e o algoritmo como um todo termina quando todos os vértices estão simultaneamente desativados e não existem mais mensagens sendo enviadas.
Após carregar a estrutura do grafo, cada nó computacional do cluster de computadores fica responsável por um conjunto de vértices do grafo, e responsável também por executar o método COMPUTE a cada supersteps para os vértices sob sua responsabilidade.
O pseudo-código abaixo apresenta o algoritmo seguindo o modelo Pregel.
Entrada: Mensagens msgs recebidas no superstep anterior.
1 procedimento COMPUTE(msgs): 2 se superstep = 0 então 3 enviar o ID do vértice para todos os vizinhos 4 senão 5 se não recebeu nenhuma mensagem então 6 votar para parar 7 senão 8 para cada mensagem msg de msgs fazer 9 se msg iniciar com o ID do vértice atual e ID for o menor da msg então 10 msg contém novo ciclo encontrado 11 senão 12 se msg não contém o ID do vértice atual então 13 inserir ID no final da lista em msg 14 encaminhar msg para todos os vizinhos
Implementação Paralela no Sistema GraphChi
[editar | editar código-fonte]Considerando que a implementação principal do modelo Pregel da Google possui código fechado, pode ser interessante avaliar uma alternativa ao modelo Pregel. Uma das alternativas é o sistema GraphChi[6] da GraphLab. Esse sistema fornece uma engine para processamento de grafos, no contexto de dados massivos, em uma única máquina. O sistema apresenta um processamento baseado em disco (memória secundária) para computação eficiente de grafos de grande escala.
Diferentemente do modelo Pregel, GraphChi é uma engine baseada em memória compartilhada. Em GraphChi, cada vértice e cada aresta armazena um dado. A comunicação entre os vértices durante o processamento paralelo é realizada com base nos dados armazenados pelos vértices e arestas.
De maneira semelhante ao modelo Pregel, GraphChi também apresenta uma abordagem centrada nos vértices. A engine do GraphChi consiste basicamente em uma sequência de iterações, nas quais, para cada vértice é executado uma função de atualização (update). Antes de cada iteração a engine executa uma função chamada before_iteration e após cada iteração é executada a função after_iteration.
A seguir é apresentado uma implementação do algoritmo de detecção de ciclos em grafos por passagem de mensagens usando o sistema do GraphChi. Esta implementação fornece uma abstração semelhante ao modelo Pregel sobre a engine do GraphChi, incluindo a abstração de passagem de mensagens, o que é conveniente para o algoritmo de detecção de ciclos proposto.
Toda aplicação do sistema GraphChi deve implementar a classe abstrata GraphChiProgram. A classe GraphChiProgram fornece os métodos públicos apresentados pelo código da classe CycleDetection a seguir.
#include "graphchi_basic_includes.hpp"
using namespace graphchi;
typedef vid_t VertexDataType;
typedef list<list<vid_t>*>* EdgeDataType;
graphchi_engine<VertexDataType, EdgeDataType> *enginePtr;
int countIteration;
size_t finishedVertices;
#define activateVertex() finishedVertices--
#define initIteration() finishedVertices = gcontext.nvertices
#define closeIteration() if(finishedVertices==gcontext.nvertices) enginePtr->set_outside_closing(true)
class CycleDetection : public GraphChiProgram<VertexDataType, EdgeDataType> {
public:
void update(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, graphchi_context &gcontext);
void before_iteration(int iteration, graphchi_context &gcontext);
void after_iteration(int iteration, graphchi_context &gcontext);
void before_exec_interval(vid_t window_st, vid_t window_en, graphchi_context &gcontext);
void after_exec_interval(vid_t window_st, vid_t window_en, graphchi_context &gcontext);
private:
void sendInitialMessageToNeighbours(graphchi_vertex<VertexDataType, EdgeDataType> &vertex);
void sendMessageToNeighbour(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, int neighbourId, list<vid_t> *value);
void deleteMessages(list<list<vid_t>*> *msgs);
bool hasInMessages(graphchi_vertex<VertexDataType, EdgeDataType> &vertex);
vid_t getMinVertexId(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, list<vid_t> *value);
bool vertexListContains(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, list<vid_t> *value);
list<vid_t> *copyVertexList(list<vid_t> *vList);
void outputCycle(list<vid_t> *value);
};
O código a seguir apresenta a implementação do método update que é equivalente à função COMPUTE do modelo Pregel. O método update é a implementação principal do algoritmo de detecção de ciclos por passagem de mensagens apresentado anteriormente pelo pseudo-código da função COMPUTE.
Basicamente, a implementação consiste em percorrer todas as arestas de entrada, recolhendo todas as "mensagens" recebidas, para poder realizar o processamento nas listas de vértices recebidas. Para cada lista de vértice recebida, é realizado o processamento sobre a lista e, caso necessário, a lista com o novo vértice é encaminhada para as arestas de saída.
void CycleDetection::update(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, graphchi_context &gcontext) {
if (countIteration == 0) {
sendInitialMessageToNeighbours(vertex);
} else {
if(hasInMessages(vertex)){
activateVertex();
}
for(int i=0; i < vertex.num_inedges(); i++) {
list<list<vid_t>*> *inMsgs = vertex.inedge(i)->get_data();
if(inMsgs && inMsgs->size()>0){
for(int j=0; j < vertex.num_outedges(); j++) {
list<list<vid_t>*>::iterator msgList;
for(msgList = inMsgs->begin(); msgList!=inMsgs->end(); msgList++){
list<vid_t> *value = copyVertexList((*msgList));
if(value->front()==vertex.vertexid){
vid_t minId = getMinVertexId(vertex, value);
if(minId==vertex.vertexid){
outputCycle(value);
}
delete value;
}else if(!vertexListContains(vertex, value)){
sendMessageToNeighbour(vertex, j, value);
}else delete value;
}
}
deleteMessages(inMsgs);
}
}
}
}
Os métodos implementados no código a seguir fornecem a implementação necessário no modelo GraphChi para oferecer uma abstração do término de execução da aplicação com base nos vértices estarem ativos ou não, semelhante ao modelo Pregel.
void CycleDetection::before_iteration(int iteration, graphchi_context &gcontext) {
initIteration();
}
void CycleDetection::after_iteration(int iteration, graphchi_context &gcontext) {
if(countIteration>0)
closeIteration();
countIteration++;
}
void CycleDetection::before_exec_interval(vid_t window_st, vid_t window_en, graphchi_context &gcontext) {}
void CycleDetection::after_exec_interval(vid_t window_st, vid_t window_en, graphchi_context &gcontext) {}
Os métodos a seguir apresentam algumas funções úteis para o algoritmo principal e algumas delas auxiliam na abstração de passagem de mensagens. Observe que o método outputCycle é apenas uma ilustração. Esse método deve receber uma lista contendo os IDs dos vértices que representam um ciclo, e executar alguma computação sobre o ciclo recebido, que melhor convir para a aplicação em questão.
void CycleDetection::sendInitialMessageToNeighbours(graphchi_vertex<VertexDataType, EdgeDataType> &vertex) {
vertex.set_data(vertex.vertexid);
for(int i=0; i < vertex.num_outedges(); i++) {
list<list<vid_t>*> *edge_value = new list<list<vid_t>*>;
list<vid_t> *msg = new list<vid_t>;
msg->push_back(vertex.vertexid);
edge_value->push_back(msg);
vertex.outedge(i)->set_data(edge_value);
}
}
void CycleDetection::sendMessageToNeighbour(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, int neighbourId, list<vid_t> *value) {
list<list<vid_t>*> *outvalue = vertex.outedge(neighbourId)->get_data();
value->push_back(vertex.vertexid);
outvalue->push_back(value);
}
void CycleDetection::deleteMessages(list<list<vid_t>*> *msgs) {
for(list<list<vid_t>*>::iterator it = msgs->begin(); it!=msgs->end(); it++){
delete (*it);
}
msgs->clear();
}
bool CycleDetection::hasInMessages(graphchi_vertex<VertexDataType, EdgeDataType> &vertex) {
for(int i=0; i < vertex.num_inedges(); i++) {
list<list<vid_t>*> *inMsgs = vertex.inedge(i)->get_data();
if(inMsgs->size()>0) return true;
}
return false;
}
vid_t CycleDetection::getMinVertexId(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, list<vid_t> *value) {
vid_t minId = vertex.vertexid;
for(list<vid_t>::iterator it = value->begin(); it!=value->end(); it++){
if( (*it)<minId ) minId = (*it);
}
return minId;
}
bool CycleDetection::vertexListContains(graphchi_vertex<VertexDataType, EdgeDataType> &vertex, list<vid_t> *value) {
list<vid_t>::iterator it = value->begin();
while(it!=value->end()){
if( (*it)==vertex.vertexid ) return true;
it++;
}
return false;
}
list<vid_t> *CycleDetection::copyVertexList(list<vid_t> *vList) {
list<vid_t> *value = new list<vid_t>;
for(list<vid_t>::iterator it = vList->begin(); it!=vList->end(); it++){
value->push_back(*it);
}
return value;
}
void CycleDetection::outputCycle(list<vid_t> *value) {
cout << "CYCLE: [ ";
for(list<vid_t>::iterator it = value->begin(); it!=value->end(); it++){
cout << (*it) << " ";
}
cout << "]" << endl;
}
GraphChi é uma solução razoável em termos de custo e benefício. Apesar de não apresentar escalabilidade em termos de nós de computação, apresenta certa escalabilidade em relação ao tamanho dos dados de entrada, devido sua característica de trabalhar em disco (memória secundária).
Experimentos
[editar | editar código-fonte]Os experimentos foram realizados em uma aplicação de exemplo, usado a implementação do sistema GraphChi, para encontrar grupos de números sociáveis[3], também chamados de aliquot cycles, estudados em Teoria dos Números. O grafo é uma representação de um subconjunto dos números naturais relacionados pela soma dos seus divisores próprios, também chamada de aliquot sum.
Grupos sociáveis são ocorrências raras nos números naturais. O primeiro grupo sociável de ordem maior ou igual a dois é o par amigável (220, 284), o segundo grupos sociável é (1184, 1210).
Experimento #1
[editar | editar código-fonte]O primeiro experimento foi executado para um grafo de 4544641 vértices. O tempo total para execução de todas as iterações foi de 70,7115 segundos (1,18 minutos), realizando um total de 64 iterações, com tempo médio de 1,08787 segundos para processar cada vértice a cada iteração.
Para esse grafo de 4544641 vértices, basicamente representando o intervalo de números naturais [0, 4544641], foram encontrados 49 grupos sociáveis de ordem maior ou igual a dois.
Experimento #2
[editar | editar código-fonte]O segundo experimento foi executado para um grafo de 13485277 vértices. O tempo total para a execução de todas as iterações foi de 326,722 segundos (5,45 minutos), realizando um total de 79 iterações, com tempo médio de 4,08402 segundos para processar cada vértice a cada iteração.
Para esse grafo de 13485277 vértices, basicamente representando o intervalo de números naturais [0, 13485277], foram encontrados 71 grupos sociáveis de ordem maior ou igual a dois.
Experimento #3
[editar | editar código-fonte]O segundo experimento foi executado para um grafo de 16875505 vértices. O tempo total para a execução de todas as iterações foi de 367,872 segundos (6,13 minutos), realizando um total de 87 iterações, com tempo médio de 4.18037 segundos para processar cada vértice a cada iteração.
Para esse grafo de 13485277 vértices, basicamente representando o intervalo de números naturais [0, 16875505], foram encontrados 76 grupos sociáveis de ordem maior ou igual a dois.
Experimento #4
[editar | editar código-fonte]O segundo experimento foi executado para um grafo de 18109729 vértices. O tempo total para a execução de todas as iterações foi de 433,687 segundos (7,23 minutos), realizando um total de 87 iterações, com tempo médio de 4,92826 segundos para processar cada vértice a cada iteração.
Para esse grafo de 18109729 vértices, basicamente representando o intervalo de números naturais [0, 18109729], foram encontrados 78 grupos sociáveis de ordem maior ou igual a dois.
Referências
[editar | editar código-fonte]- ↑ 1,0 1,1 http://pt.wikipedia.org/wiki/Busca_em_profundidade
- ↑ 2,0 2,1 Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest and Clifford Stein, Introduction to Algorithms, The MIT Press, 3rd Ed. (2009).
- ↑ 3,0 3,1 3,2 ROCHA, Rodrigo C. O., A Method of Searching Sociable Numbers Using Graph Theory: An Implementation on Large Computer Clusters, (2013).
- ↑ Grzegorz Malewicz, Matthew H. Austern, Aart J.C Bik, James C. Dehnert, Ilan Horn, Naty Leiser and Grzegorz Czajkowski, Pregel: a system for large-scale graph processing, Proceedings of the 2010 ACM SIGMOD International Conference on Management of Data, SIGMOD '10 (2010), 135--146.
- ↑ John A. Bondy, Uppaluri S. R. Murty, Graph Theory, Springer, 1st Ed. (2008).
- ↑ Aapo Kyrola, Guy Blelloch, and Carlos Guestrin, GraphChi: Large-scale graph computation on just a PC, OSDI (2012).
