Processamento de Dados Massivos/Projeto e implementação de aplicações Big Data/Agrupamento baseado em densidade
Descrição
[editar | editar código-fonte]Denominação
[editar | editar código-fonte]Agrupamento de dados massivos baseado em densidade.
Contexto
[editar | editar código-fonte]A mineração de dados é uma área da computação que visa a análise de dados para extração de informação e conhecimento. As tarefas de mineração podem ser divididas em supervisionadas, quando são usados registros conhecidos para o aprendizado de máquina, e não-supervisionada quando não há uso de registros para induzir os resultados.
O agrupamento é uma tarefa não-supervisionada de mineração de dados que consiste em dividir os registros da base de dados em grupos de forma a deixar os mais similares entre si em grupos iguais e os menos similares em grupos distintos. Essa tarefa possui inúmeras aplicações, dentre as quais pode-se destacar os sistemas de recomendação, predição de funções proteicas e resolução de entidades.
Três dos principais algoritmos de agrupamento são o K-means [1] , o Expectation Maximization - EM [2] e o DBScan [3]. Ao contrário do DBScan, o K-Means e o EM são algoritmos que exigem como parâmetro o número de grupos a serem formados e não são capazes de formar grupos com formatos arbitrários, além de serem sensíveis à presença de exceções. Porém o DBScan é o algoritmo mais caro entre eles: apresenta custo quadrático em relação ao tamanho da base.
Considerando que essa abordagem baseada em densidade é fundamental para algumas aplicações, como por exemplo, quando o número de grupos não é conhecido ou quando há exceções na base, e se observado o crescente volume de dados disponíveis, torna-se desejável a utilização desse algoritmo para suportar dados massivos de forma que o agrupamento possa ser realizado com eficiência e escalabilidade.
Algoritmo
[editar | editar código-fonte]O DBScan é um algoritmo de agrupamento baseado em densidade de registros por região, o que permite a formação de grupos não-convexos e com formatos arbitrários. A figura 1 mostra um exemplo de registros que só podem ser agrupados corretamente utilizando-se esse algoritmo devido ao formato arbitrário dos grupos.

Essa técnica recebe dois valores como parâmetros: o valor de corte D que indica a distância máxima que dois pontos podem estar para eles serem considerados vizinhos e o número mínimo de vizinhos N que um ponto deve ter para ser considerado um ponto de centro, conforme será mostrado.
A definição de vizinhança V nesse contexto para um determinado ponto P é dada pelo conjunto de pontos que estão a uma distância d menor ou igual a D, ou seja,
V(P) = {Y | d(P,Y) <= D}.
A principal limitação em termos de eficiência do DBScan é a sua primeira etapa que consiste em calcular a distância entre todos os pares possíveis de registros da base B para definir quantos vizinhos cada um possui e então classificá-los como ponto de centro, ponto de borda ou exceção. Os pontos de centro são aqueles que possuem N ou mais vizinhos. Os pontos de borda não possuem N ou mais vizinhos mas são vizinhos de um ponto de centro. Os registros considerados exceções possuem menos de N vizinhos e não são vizinhos de nenhum ponto de centro. A figura 2 ilustra as três classificações que um ponto pode receber nesse algoritmo.

Após essa etapa de classificação, os pontos de centro são percorridos e seus vizinhos são assimilados a seu grupo. Se um dos vizinhos do ponto de centro que está sendo percorrido for outro ponto de centro X, o algoritmo passa a percorrer os vizinhos de X. Observa-se que a ordem de percorrimento dos pontos de centro não alteram a disposição dos pontos de centro entre os grupos, porém pode influenciar na assimilação dos pontos de borda aos grupos. Os pontos exceções não são assimilados a nenhum grupo, independente da ordem de percorrimento. O algoritmo abaixo mostra os passos executados pelo DBScan conforme [4].
DBScan(B, D, N):
Para cada registro P em B {
Computa os vizinhos de P;
Classifica P;
}
grupoAtual = 0;
Para cada ponto de centro P não visitado {
grupoAtual++;
Assimila(P, grupoAtual);
}
Retorna resultado do agrupamento;
Assimila(P, grupoAtual):
Assimila P ao grupo grupoAtual;
Para cada vizinho Q de P {
Assimila Q ao grupo grupoAtual;
Se Q é ponto de centro {
Assimila(Q, grupoAtual);
} }
Quanto ao armazenamento, a implementação original do DBScan utiliza a estrutura R*-tree [5] para manter todos os registros em memória secundária.
Exemplo de funcionamento
[editar | editar código-fonte]Essa seção mostra passo-a-passo como o DBScan realiza o agrupamento para os dados mostrados na figura 3 com parâmetros de distância e número mínimo de vizinhos iguais a e , respectivamente.
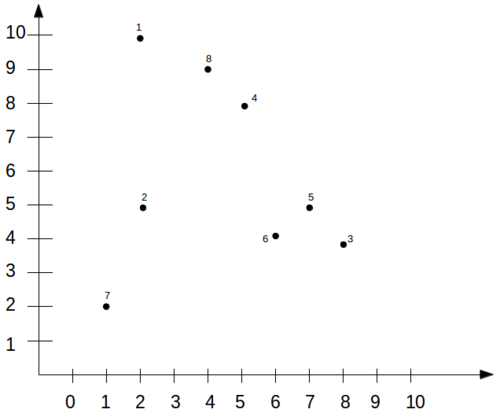
Inicialmente, a distância entre os pares de registros são calculados. Os valores estão mostrados na tabela abaixo.
| Ponto | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1 | 0 | |||||||
| 2 | - | 0 | ||||||
| 3 | - | - | 0 | |||||
| 4 | - | - | - | 0 | ||||
| 5 | - | - | - | - | 0 | |||
| 6 | - | - | - | - | - | 0 | ||
| 7 | - | - | - | - | - | - | 0 | |
| 8 | - | - | - | - | - | - | - | 0 |
A medida que os pares de pontos têm suas distâncias calculas, os pontos são classificados como ponto de centro, de borda, ou exceção. Observa-se que nesse exemplo para dois pontos serem considerados vizinhos eles devem estar a uma distância menor ou igual a . O resultado da classificação está mostrado abaixo.
| Classificação | Pontos |
|---|---|
| Pontos de centro | 3,5,6,8 |
| Pontos de borda | 1,4 |
| Exceções | 2,7 |
Na segunda fase do DBScan, os pontos de centro são percorridos. O primeiro grupo criado possui o ponto de centro 3 e durante o percorrimento de seus vizinhos, os pontos 5 e 6 são assimilados a esse grupo. O segundo grupo criado possui inicialmente o ponto de centro 8 e a medida que seus vizinhos são perridos, os pontos 1 e 4 também são assimilados a ele. Os pontos 2 e 7 não são vizinhos de nenhum ponto de centro e por isso não são assimilados a nenhum grupo. A figura 4 mostra o resultado do agrupamento para esse exemplo.

Requisitos
[editar | editar código-fonte]Os principais requisitos para a execução distribuída ou em paralelo do DBScan são a escalabilidade, o balanceamento e a tolerância a falhas.
Escalabilidade
[editar | editar código-fonte]A escalabilidade é um fator fundamental nesse contexto de algoritmos para dados massivos. Para que a escalabilidade seja satisfeita, é necessário garantir que não haja gargalos, ou seja, a memória, o processador e a rede de todos os nós devem estar trabalhando com a mesma carga, sem ociosidade em espera por outro evento.
Balanceamento de carga
[editar | editar código-fonte]O balanceamento de carga é um dos fatores que contribui para escalabilidade. A divisão desbalanceada dos dados e tarefas entre os nós em uma abordagem distribuída tem como consequência a formação de gargalos e ociosidade, que deixariam ineficiente a aplicação para dados massivos.
Tolerância a falhas
[editar | editar código-fonte]A tolerância a falhas é importante para o agrupamento distribuído pois a ausência de alguns registros no processo tem o poder de influenciar a qualidade do resultado. Na maioria das aplicações voltadas para dados massivos, a tolerância de falhas é satisfeita com a replicação de registros em diferentes nós e com a projeção de algoritmos que não possuem um único ponto de falha.
Paralelizações existentes
[editar | editar código-fonte]Esta seção descreve como o a implementação do DBScan já foi realizada para suportar grandes volumes de dados.
Em [6] é apresentado uma implementação paralela do DBScan com uma abordagem mestre-escravo: enquanto o núcleo mestre realiza a etapa de assimilação de grupos, os escravos respondem a consultas de vizinhança usando a estrutura R*-Tree para armazenamento.
Em P-DBSCAN [7] , a base é particionada e o agrupamento é feito de forma independente entre os nós de forma distribuída. Ao final, há uma agregação dos resultados de cada nó para formar o resultado final. Quanto ao armazenamento, a estrutura utilizada é a Priority R-Tree [8] que é uma variação eficiente da R-Tree. Nessa implementação há a limitação de haver um único nó para juntar os resultados do agrupamento feito por todos os nós. Além disso, os pontos considerados exceções por um nó não são tratados posteriormente na junção dos grupos, portanto grupos densos podem ser perdidos se seus registros estiverem divididos entre os nós.
De forma similar ao P-DBSCAN, o MR-DBSCAN [9], proposto em , é uma implementação distribuída do DBScan com quatro estágios e que utiliza o paradigma Map-reduce [10]. A primeira etapa consiste em dividir a base entre os nós de forma balanceada e de forma a deixar os registros mais próximos no mesmo nó. Em seguida, na fase map, o DBScan é executado de forma independente dentro de cada nó. A terceira etapa é a fase reduce: todos os nós são analisados para descobrir em quais situações o mesmo nó foi agrupado para diferentes grupos, ou seja, é feito um mapeamento da junção e remarcação dos grupos que é realizada na quarta e última etapa. Os resultados mostraram que a escalabilidade e a eficiência dessa abordagem são bastante satisfatórias.
Em SDBDC [11] , que é uma melhora do DBDC [12] , também é realizada a tarefa de agrupamento baseada em densidade de forma distribuída. Nessa abordagem, os pontos centrais de cada nó são determinados e a partir deles, os pontos representativos globais são identificados. A partir dessa informação sobre os pontos representativos globais, os pontos de cada nó são rotulados para os grupos. Portanto essa técnica parte de uma informação local para gerar uma análise global e novamente gerar uma informação local. Há a possibilidade do usuário balancear a quantidade de pontos considerados representativos em cada nó, o que pode aumentar o tempo de execução e a qualidade ou realizar uma execução mais rápida com menos qualidade.
Considerando os trabalhos existentes de paralelização do DBScan, conclui-se que o agrupamento distribuído baseado em densidade não é uma tarefa trivial e há vários fatores a serem balanceados já que é inviável atender a todos. Alguns desses fatores são a comunicação, a descentralização de tarefas, a completude e a qualidade da solução.
Se há muita centralização das tarefas, perde-se em escalabilidade porém há ganhos quanto à completude e à qualidade do agrupamento. Por exemplo, se o agrupamento é feito de forma independente entre os nós para que depois haja uma união centralizada dos grupos, quanto mais informações for considerada de cada nó, maior será a qualidade, porém menor será a eficiência. Por exemplo, se os pontos considerados exceções não forem considerados nessa etapa de união dos grupos, pode-se perder informações sobre os grupos que poderiam ser formados se esses pontos estivessem juntos. Por outro lado, a escalabilidade da aplicação seria comprometida se esses pontos fossem considerados.
A comunicação é outro fator que se comporta de forma similar à centralização: quanto mais comunicação, maior será o overhead da aplicação, porém melhor a qualidade dos resultados. Em nenhum dos trabalhos vistos houve uso de comunicação durante o processo de execução do algoritmo nos nós.
Portanto, como o agrupamento baseado em densidade depende de informações globais sobre vizinhança entre os pontos e a implementação paralela ou distribuída deve ser capaz de encontrar um balanceamento entre agregação dos dados globais (centralização ou comunicação), eficiência e qualidade.
Projeto
[editar | editar código-fonte]Essa seção descreve o projeto de implementação da abordagem distribuída do DBScan. Para essa análise, o algoritmo será tratado por duas etapas: a primeira é o cálculo da distância entre todos os pares possíveis de registros e a segunda é a etapa de percorrimento dos pontos centrais e assimilação de pontos aos grupos.
Oportunidades de paralelização
[editar | editar código-fonte]A primeira etapa é a mais custosa do algoritmo e representa uma oportunidade de paralelismo já que pode ser feita de forma independente entre todos os pares, sendo que um cuidado a ser tomado é garantir a completude e a não-redundância na distribuição dos pares. O paradigma Map-reduce pode ser considerado uma solução aderente, em que a fase map seria o cálculo das distâncias entre todos os pares e a etapa reduce seria a classificação dos pontos como ponto de centro, ponto de borda ou exceção. O objetivo final dessa etapa é ter a informação sobre quais pontos são vizinhos e qual a classificação de cada ponto.
Outra solução de paralelismo para a primeira etapa seria dividir os registros entre os nós e calcular apenas a distância dos pares de registros de cada nó de forma independente. Tratando-se de grandes volumes de dados, essa segunda abordagem é mais adequada, já que a primeira resultaria em um grande volume de informações sobre vizinhança, o que tornaria inviável a consulta e a distribuição dessas informações para todos os nós.
Em uma abordagem distribuída, a paralelização da segunda etapa só pode ser feita dividindo-se os registros entre os nós e executando a etapa de percorrimento dos pontos centrais e assimilação dos grupos de forma independente dentro de cada um. A variação nesse processo ocorre na quantidade de registros distribuídos por nó.
Padrão de acesso aos dados
[editar | editar código-fonte]Quando o agrupamento é realizado com base na densidade de registros, é necessário manter e consultar a informação sobre quais registros são vizinhos, qual a classificação de cada ponto e quais pontos já foram agrupados e para qual grupo. Essas informações podem ser armazenadas ou de forma centralizada com uso de memória compartilhada ou de forma distribuída. Mais uma vez, o fato do algoritmo ser distribuído e direcionado para grandes volumes de dados torna inviável o uso de memória compartilhada. O controle de acesso e escrita tornaria essa atividade um gargalo para execução. Portanto as informações devem estar distribuídas entre os nós e é desejável que haja particionamento dos dados devido ao grande volume de dados para armazenamento.
Padrão de comunicação
[editar | editar código-fonte]A comunicação do DBScan distribuído deve ocorrer no momento em que os grupos são formados. Para isso há duas possibilidades: realizar a comunicação entre os nós durante a etapa de assimilação dos grupos ou realizar o agrupamento sem comunicação entre os nós para depois realizar uma operação de junção dos grupos considerando os grupos formados por todos os nós.
Linha do tempo integrada
[editar | editar código-fonte]A figura 5 resume a linha do tempo considerando as possibilidades discutidas para a implementação do DBScan distribuído.

Considerando a proposta exploratória e investigativa do trabalho e voltada para grandes volumes de dados, a solução escolhida consiste em dividir os dados em blocos, distribuindo entre os nós apenas os dados referentes a seus pontos e fazendo uso de comunicação na realização do agrupamento. A proposta de calcular a distância de todos os pares possíveis tornaria essa etapa um gargalo, principalmente em termos de armazenamentos se aplicada a dados massivos. Já a proposta de realizar agrupamento de forma independente para depois unir os grupos foi realizada em dois dos trabalhos mais relevantes com a mesma proposta. Portanto, dentre as opções que não tornam a primeira etapa um gargalo para a execução, foi escolhida a opção ainda não explorada.
Desenvolvimento
[editar | editar código-fonte]Essa seção descreve com mais detalhes a proposta de agrupamento distribuído para grandes volumes de dados para que as decisões do projeto permitam sua implementação independentemente das ferramentas e plataformas.
Estratégias de paralelização
[editar | editar código-fonte]Conforme mostrado, a primeira etapa do algoritmo consiste em calcular a distância entre os pares de pontos, o que é uma tarefa custosa, com complexidade quadrática em termos do número de registros. A proposta de dividir os pontos em blocos e calcular apenas a distância intra bloco torna essa tarefa escalável e eficiente.
Esse paralelismo de dados será aplicado também na segunda etapa: cada nó vai executar o DBScan de forma independente considerando apenas a distância entre os pontos recebidos e calculada na primeira etapa. Como cada nó terá informações apenas de seus registros, a comunicação deve garantir que as informações seja transmitidas com algum critério para definir a granularidade na transmissão de informações.
Um cuidado a ser tomado é que a qualidade do agrupamento final dependerá diretamente de como os dados foram particionados em blocos: se os blocos apresentarem pontos muito distantes entre si, os nós formarão poucos grupos e encontrarão muitas exceções, conforme mostrado na figura 6, em que cada quadrado representa um nó de processamento e os pontos vermelhos representam pontos que poderiam ter formado um grupo, mas não estavam em quantidade suficiente em nenhum dos nós para tal. Conforme será mostrado, uma estratégia para reduzir a probabilidade de ocorrer essa situação é replicar os pontos nos nós.

Para que essa condição seja satisfeita, o particionamento dos dados é feito com a função Z-order curve que mapeia dados multi-dimensionais para apenas uma dimensão preservando a localidade dos registros. O grande risco é de que um gargalo seja formado: caso essa etapa de pré-ordenaçao dos dados para definir o paticionamento não seja implementada de forma eficiente, a replicação dos dados será a única alternativa para evitar que situações como a da figura [exemplo] ocorram. Uma abordagem map-reduce também poderá ser aplicada no particionamento caso essa etapa esteja comprometendo a escalabilidade da aplicação.
Estratégias de armazenamento
[editar | editar código-fonte]Como em algumas aplicações a eficiência é mais importante que a precisão do agrupamento e em outras o inverso ocorre, desejou-se algum mecanismo que permita o balanceamento entre qualidade e tempo de execução no armazenamento. A solução encontrada foi a divisão do espaço dimensional e a possibilidade de replicação de registros entre os nós.
A divisão do espaço dimensional deve ser realizada de maneira similar ao espaço do CAN [13] , uma rede par a par proposta em . Com essa divisão, a aplicação não armazena e transmite informações de cada ponto, o que seria ineficiente para dados massivos: as informações trocadas são referentes às partições e a granularidade do particionamento será um parâmetro do programa.
O outro mecanismo para permitir esse balanceamento entre tempo de execução e qualidade e ainda garantir tolerância a falha é a replicação de pontos em diferentes nós. Nesse caso, um parâmetro de execução define quantas vezes cada ponto será replicado entre os nós. Além de aumentar a tolerância a falhas de nós, esse parâmetro ajuda a evitar situações em que vários pontos vizinhos ficam espalhados e por isso não formam um grupo ao final da execução.
A figura 7 mostra todas as informações que um nó precisa armazenar. Nesse exemplo com duas dimensões, o nó deverá armazenar informações sobre quais dos seus pontos são vizinhos, a classificação de cada ponto (de centro, de borda ou exceção) e quais partições já foram assimiladas a um grupo. A informação sobre os grupos formados deve ser a mesma em todos os nós: os grupos marcados de amarelo e azul foram informados por outros nós.

Estratégia de comunicação
[editar | editar código-fonte]A comunicação deve ser realizada para informar e sincronizar informações sobre quais partições foram assimiladas a qual grupo. Nesse caso, não é necessário direcionar as mensagens, elas devem ser enviadas para todos. Também não é necessário sincronização ou uso de barreiras: se dois nós enviam mensagem ao mesmo tempo informando que a mesma partição pertence a um de seus grupos, cada nó deve saber interpretar a informação baseando-se no tipo de ponto que levou à assimilação da partição ao grupo. Portanto, a cada vez que um ponto é assimilado a um grupo, o nó deve enviar uma mensagem avisando qual o tipo desse ponto e qual partição foi assimilada a qual grupo.
Se dois ou mais nós enviarem mensagem informando que uma partição contendo pelo menos um ponto de centro pertence a um determinado grupo, a interpretação de todos os nós devem ser de que esses grupos devem ser unidos. A figura 8 representa essa situação: a partição (2,3) foi assimilada para dois grupos diferentes no primeiro e no terceiro nó. Após o recebimento da mensagem informando que aquela partição contendo um ponto de centro foi assimilada para os grupos A e B, todos os nós fazem a junção desses grupos.

Se essa situação ocorrer apenas com partições de borda, os nós devem manter a informação processada por último. Nesse caso haverá nós armazenando diferentes grupos para a mesma partição e apenas ao final, quando haverá a produção do resultado final, será definido a qual grupo a partição de borda pertence. Essa situação em que a definição de um ponto de borda não é determinística também ocorre no DBScan tradicional, já que a ordem de execução dos pontos centrais pode fazer com que os pontos de borda sejam assimilados a grupos distintos. Essa situação está ilustrada na figura 9.

Implementação
[editar | editar código-fonte]Essa seção descreve a implementaçao em andamento da aplicação.
Plataformas e ferramentas
[editar | editar código-fonte]A implementação da aplicação faz uso do framework Apache Hadoop [14], implementado na linguagem Java e usando-se o módulo Hadoop Distributes File System para armazenamento. A comunicação utiliza RMI – Remote Method Invocation, uma interface de programação que permite a execução de chamadas remotas, na qual um objeto ativo em uma máquina virtual Java pode interagir com objetos ativos de outros nós. Mais detalhes da implementação serão apresentadas quando a mesma for concluída.
Integração de plataformas e ferramentas
[editar | editar código-fonte]Detalhes de implementação
[editar | editar código-fonte]Seguem os detalhes e algumas definições realizadas durante a fase de implementação.
- A identificação dos grupos deve unívoca. A solução com números sequenciais para todos os nós pode representar um problema se dois nós criarem grupos ao mesmo tempo, portanto cada nó deve ter sua própria sequência de identificadores de grupos. Além disso, cada nó tem um identificador único e a identificação dos grupos é feita a partir da concatenação do identificador único do nó com o número de sequência atual do nó. Por exemplo, o segundo grupo do nó nomeado ID4 é identificado por ID4.2.
- Quando dois grupos são unidos, o novo grupo formado é nomeado com a concatenação dos grupos que deram origem a ele. Por exemplo se o grupo ID4.2 e ID9.7 forem unidos, o grupo resultante será identificado por ID4.2.ID9.7.
Avaliação
[editar | editar código-fonte]Após a conclusão da implementação do código, a avaliação da aplicação será realizada utilizando uma base de dados contendo informações sobre filmes disponibilizada pelo Netflix em uma competição de sistemas de recomendação. A base contém aproximadamente 100 milhões de registros com avaliações de filmes.
Carga de trabalho
[editar | editar código-fonte]Avaliação experimental
[editar | editar código-fonte]Análise de resultados
[editar | editar código-fonte]Análise Crítica
[editar | editar código-fonte]Conclusão
[editar | editar código-fonte]O projeto descrito visa a implementação do algoritmo de agrupamento DBScan distribuído e com o propósito de tratar grandes volumes de dados.
Conforme mostrado na revisão bibliográfica, a maioria dos trabalhos existentes com a mesma proposta realizam o agrupamento de forma independentes entre os nós para depois realizarem a união e o tratamento da fronteira entre os grupos criados pelos múltiplos nós. A proposta desse trabalho é realizar o agrupamento dividindo-se os registros entre os nós, e agrupá-los utilizando comunicação para informar quais partições foram assimiladas a quais nós. Conforme mostrado na seção "Desenvolvimento", há duas possibilidades para o controle de eficiência e qualidade: a granularidade da divisão do espaço e a quantidade de vezes que cada registro é replicado. A principal ferramenta de implementação é o framework Apache Hadoop e ao final dessa etapa, a avaliação será realizada com uma grande base de dados de filmes.
Espera-se que ao final do processo o resultado seja uma aplicação escalável e eficiente para agrupar com qualidade grandes volumes de dados, além de publicações acadêmicas na área de big data.
Referências
[editar | editar código-fonte]- ↑ K-Means,
- ↑ Expectation–maximization,
- ↑ DBScan,
- ↑ Data Mining and Analysis:Foundations and Algorithms
- ↑ R*-tree,
- ↑ Experiments in parallel clustering with dbscan, .
- ↑ P-DBScan
- ↑ The priority r-tree: A practically eficient and worst-case optimal r-tree, .
- ↑ MR-DBScan,
- ↑ Map-reduce
- ↑ Scalable Density Based Distributed Clustering, .
- ↑ Density Based Distributed Clustering,
- ↑ Content Addressable Network
- ↑ Apache Hadoop.




















