Introdução à física/Dinâmica/Decomposição de vetores
A decomposição de vetores envolve ângulos relacionados aos vetores.
Decomposição de um vetor
[editar | editar código-fonte]A respeito da direção de um vetor relacionado à trajetória, tem-se os seguintes fatos:
- Se um vetor é paralelo à trajetória, o vetor resultante é equivalente ao próprio vetor;
- Se um vetor é perpendicular à trajetória, o vetor resultante é igual a zero;
- Se um vetor está disposto a ângulos diferentes de 0° ou x90° (para ) em relação à trajetória, deve-se realizar a decomposição do vetor.
Sobre um plano inclinado
[editar | editar código-fonte]Conforme as leis postuladas por Newton, pode-se dizer que:
- Um corpo de massa m possui força peso igual a mg (segunda lei de Newton);
- A uma superfície em que um corpo aplica uma força, será aplicada uma força contrária de igual intensidade (terceira lei de Newton).

Como a força peso (W na imagem) é aplicada pela Terra, esta estará sempre direcionada ao centro do planeta. Portanto, em tais casos, a força peso não é totalmente aplicada na superfície, e parte dela gera movimento, geralmente fazendo os corpos escorregarem. Assim, para se calcular a força que é aplicada na superfície, deve-se considerar um vetor perpendicular ao plano (mgcosθ no diagrama abaixo). Já a força resultante, deve-se considerar um vetor paralelo ao plano (mgsinθ no diagrama).

Temos, então, pela simplificação de mg = P:
Onde:
- FR é a força resultante (paralela à superfície) e que geralmente provoca movimento;
- P é a força peso (direcionada ao centro do planeta), equivalente a mg (produto da massa pela aceleração gravitacional);
- N é a força aplicada na superfície (perpendicular à superfície), denominada normal.
Aplicando a terceira lei de Newton, aliada às leis da geometria, a seguinte equação é verdadeira:
E então,
Para os ângulos, temos duas fórmulas que podem ser usadas:
|
|
|
Demonstração
[editar | editar código-fonte]Um objeto de massa 10 kg é abandonado em uma superfície perfeitamente lista, e que forma o ângulo de 45° com a superfície. Dados: g = 10; cos45° = 0,5√2; sen45° = 0,5√2.
- a) Qual a força que o objeto exerce sobre a superfície?
- b) Qual a força resultante?
- Pode ser dada por:
- E como já se sabe o valor de N, pode-se resolver também por:
- c) Qual a aceleração do objeto?
Para resultante angular
[editar | editar código-fonte]
Já no caso de se ter o vetor (A) em um sentido, mas o vetor resultante (R) é angular (ou vice-versa), pode-se usar uma das fórmulas abaixo. Esses casos não ocorrem necessariamente em um plano inclinado.
|
|
|
| E com o vetor A em evidência: | |
|
|
|
| Se o ângulo for desconhecido: | |
|
|
|
Pode-se considerar, também:
Demonstração
[editar | editar código-fonte]- a) Em um sistema isolado, um objeto encontra-se encostado a uma rampa perfeitamente lisa, que forma ângulo de 60° com a superfície. Tal objeto adquire energia cinética equivalente a 10 joules, e se move na direção da rampa. Considerando o cosseno de 60 igual a 0,5, qual a energia cinética aproveitada (resultante)?
Decomposição de dois vetores
[editar | editar código-fonte]Pela terceira lei de Newton, podemos ter as seguintes conclusões a respeito de um ângulo em um vetor:
- Se dois vetores estão na mesma direção e sentido, eles se somam;
- Se dois vetores estão dispostos a 180° um do outro, subtrai-se os valores dos respectivos vetores.
- Se dois vetores estão dispostos a ângulos diferentes de 0° ou 180°, utiliza-se a regra do paralelogramo.
Vetor resultante
[editar | editar código-fonte]Pela imagem a seguir, analise a presença de dois vetores, A e B, e de um ângulo α entre estes.

O vetor resultante é dado pela regra do paralelogramo:
E caso se deseje o ângulo:
Quando A = B, e α = 90°, pode-se utilizar uma versão mais simples para a resultante:
Demonstração
[editar | editar código-fonte]Sobre um objeto, atuam duas forças simultâneas, uma de 2 newtons e outra de 3 newtons. Entre as forças, está um ângulo de 60°. Qual a força resultante? Considere cos 60 = 0,5.
Solução:
Ângulo resultante
[editar | editar código-fonte]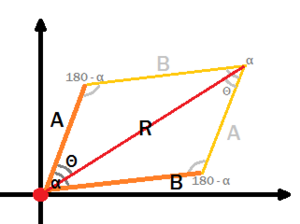
Consideraremos como ângulo resultante (θ) o ângulo entre o vetor resultante (R) e o vetor A. Pode ser descoberto pela seguinte fórmula:
Quando A = B, pode-se descobrir o ângulo da resultante, também, por:
Vetor em evidência
[editar | editar código-fonte]| Você já viu o modo em que se deixa R, α e θ em evidência. Mas como deixar A ou B em evidência? Através da lei dos senos, chegaremos a uma das seguintes fórmulas: | |||
|
|
|
|
|
E caso A = B e α = 90:
Demonstração
[editar | editar código-fonte]Atuam em um corpo duas força (A e B) simultaneamente e no mesmo plano. Tais forças estão dispostas a 60° uma da outra, e a resultante (equivalente a 10 newtons) está disposta a 30° da força A. Qual a intensidade da força A? Considere o seno de 30° igual a 0,5 e o seno de 120° igual a 0,5 √3.
Decomposição de vários vetores
[editar | editar código-fonte]Por fórmulas conjuntas
[editar | editar código-fonte]
Quando temos vários vetores, devemos aplicar as fórmulas anteriores conjuntas. Na figura acima, temos três vetores (A, B e C). Para descobrirmos a resultante dos três vetores, consideraremos, primeiramente, dois vetores (A e B) e calculemos a resultante destes (R1 na figura). Depois, consideremos R1 como um vetor e calculemos a resultante com C, e finalmente obteremos o resultado. Como usaremos incógnitas para o problema, as fórmulas a seguir, podem, sim, serem utilizadas para qualquer valor, desde que haja três vetores.
- I - A resultante de A e B, R1, é dada por:
- II - Utilizando I, podemos descobrir o ângulo da resultante R1 (θ):
- III - Descubramos o ângulo que R1 faz com C:
- IV - Consideraremos R1 como vetor, e calculemos a resultante total com C (utilizando o ângulo em III):
E esta é a resultante dos vetores.
Demonstração
[editar | editar código-fonte]Sobre um objeto são aplicadas três forças simultâneas, A, B e C, de módulos 6, 10 e 16 newtons, respectivamente. O ângulo que A forma com B é equivalente a 60°, enquanto que B forma ângulo de graus com C. Qual a resultante das forças? Considere o cosseno de 60° igual a 0,5, e o seno de 120° a .
- I)
- II)
- III)
- IV)
Assim, a resultante das forças é 26 newtons.
Pelo teorema de Lammy
[editar | editar código-fonte]Pelo teorema de Lammy, se tem um metódo muito prático para cálulo. Este é utilizado para o equilíbrio dos corpos rígidos. Neste, se faz o uso da lei dos senos. Veja, abaixo, seu funcionamento. Utilizaremos as mesmas incógnitas que o caso acima.
Você deve notar que:
- Não há resultante no cálculo, logo, este teorema somente deve ser aplicado quando R = 0;
- Como o teorema é baseado na lei dos senos, é inadimissível haver determinada quantidade de vetores, senão três.
Aplicação na dinâmica
[editar | editar código-fonte]A decomposição de vetores é essencial na maioria de questões de dinâmica. Para que se consiga uma relação que obedeça a terceira lei de Newton, geralmente se decompõe as forças na mesma direção da aceleração ou perpendicular a ela, por simplicidade de cálculos, pois caso contrário, seria necessário decompor também a aceleração.
Exercícios
[editar | editar código-fonte]Você pode fazer exercícios sobre decomposição de vetores clicando aqui.













































