Teoria de números/Congruências
Carl Friedrich Gauss
 Carl Friedrich Gauss foi um famoso matemático, astrônomo e físico alemão. |
| Este módulo tem a seguinte tarefa pendente: Incluir breve biografia sobre Carl Friedrich Gauss, enfatizando suas contribuições na teoria de números. |
Definição[editar | editar código-fonte]
- Definição
O inteiro é dito congruente ao inteiro módulo , quando . Neste caso, escreve-se .
Com essa notação, tem-se para quaisquer inteiros :
pois
e
Como se pode ver na próxima tabela, onde são listadas todas as combinações possíveis para e módulo , a soma de dois quadrados nunca é congruente a módulo .
| 0 | 1 | |
|---|---|---|
| 0 | 0 | 1 |
| 1 | 1 | 2 |
Em outras palavras, o simples cálculo feito acima mostra que ao somar dois quadrados perfeitos, o sucessor do resultado nunca é múltiplo de .
- Nota
Sendo assim, a notação para congruências, introduzida por Gauss evita o uso de várias constantes () que não são relevantes durante grande parte dos cálculos envolvendo divisibilidade. Atente para a semelhança (visual) entre as seguintes expressões:
- Observação
Conforme o algoritmo da divisão, dados e existem únicos de modo que:
- , com
Isso significa que qualquer inteiro é congruente ao seu resto na divisão por um inteiro não nulo . Uma vez que o resto obtido é único, pode-se definir para cada inteiro fixado, uma função que a cada número associa o resto da divisão de por . A imagem de por esta função é denotada por . Mais precisamente:
Quando não houver risco de confusão, o índice será omitido e será escrito apenas em vez de .
A congruência vista como uma relação de equivalência[editar | editar código-fonte]
A partir da noção de congruência módulo um certo inteiro , pode-se definir uma relação sobre o conjunto dos números inteiros da seguinte forma:
Como será mostrado logo a diante, a relação assim definida satisfaz as propriedades de reflexividade, simetria, transitividade. Sendo, por isso, considerada uma relação de equivalência:
De modo geral, é sempre possível construir uma relação de equivalência sobre um conjunto a partir de uma função cujo domínio seja . De fato, se for definido que:
então será uma relação de equivalência em , pois :
E destas propriedades da igualdade seguem as propriedades correspondentes para a relação . Em particular, tomando , e , conclui-se que a congruência é uma relação de equivalência.
Compatibilidade com as operações[editar | editar código-fonte]
Um fato importante, que não pode deixar de ser mencionado é que a relação de congruência é compatível com as operações do anel dos números inteiros, a saber, a adição e a multiplicação. Uma operação é compatível com uma relação de equivalência quando a partir de
pode-se concluir que
No caso da relação de congruência, vê-se que a mesma é compatível tanto com a adição quanto com a multiplicação de números inteiros, como é sintetizado no próximo resultado.
- Teorema
Se são números inteiros tais que:
A verificação deste resultado é bem simples, como se pode ver a seguir.
| Demonstração |
|---|
| Primeiramente, da hipótese sobre os inteiros , segue que existem inteiros , tais que
Donde,
ou seja,
Além disso, onde Logo, ou seja, |
O anel das classes de congruência[editar | editar código-fonte]

Sempre que se tem uma relação de equivalência sobre um conjunto é possível definir uma partição de tal conjunto. Uma coleção de subconjuntos de é chamada de partição de se todo elemento de pertence a exatamente um elemento de . Os elementos de são disjuntos dois a dois, e sua união é o próprio conjunto .
Para definir uma partição de , usando a congruência módulo , primeiramente define-se para cada inteiro a classe de equivalência de , segundo , como:
Quando o inteiro estiver subentendido, será utilizado apenas para denotar .
Nesses termos, o quociente de pela relação é a partição dada por:
Por simplicidade, denota-se simplesmente como .
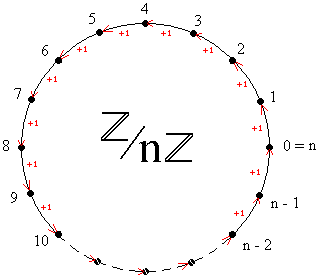
Uma das formas de visualizar essa partição de é imaginar que sobre um barbante foram marcados todos os números inteiros, separando os números adjacentes sempre por uma mesma distância. Depois disso, para obter uma representação de , enrola-se o barbante em torno de uma circunferência (infinitas vezes!), de modo que o zero ocupe a mesma posição que os inteiros . Você pode então pensar nos elementos de como sendo os n pontos sobre a circunferência que se formou. Veja uma ilustração:
Deste modo, cada ponto da circunferência representa uma das classes de equivalência módulo , ou seja, o conjunto dos números inteiros que ficaram sobrepostos naquele ponto da circunferência.
Mas o que há de interessante em particionar o conjunto dos números inteiros?
A grande utilidade de separar os números inteiros em várias classes de congruência é consequência da compatibilidade da congruência com as operações de adição e multiplicação: Sabendo-se que elas são compatíveis, é possível definir em cada novas operações de adição e multiplicação. O procedimento é o seguinte:
Fixado um inteiro , e dadas as classes , define-se:
- (ou simplesmente )
Em outras palavras, a soma (produto) das classes de congruência dos inteiros é a classe de congruência de sua soma (produto).
É importante notar onde é utilizada a compatibilidade da congruência com as operações de : Dadas duas classes de equivalência e , tanto faz obter como sendo ou . Todas essas classes são idênticas!
Mais do que isso, ao definir essas operações, torna-se um anel com unidade, ou seja, são válidas as seguintes propriedades:
Além disso, tem-se um homomorfismo de anéis entre e :
- Recordando...
- Um anel com unidade é um conjunto R equipado com duas operações binárias + : R × R ? R e · : R × R ? R (onde × denota o produto cartesiano), chamadas de adição e multiplicação, tais que:
- (R, +) é um grupo abeliano com elemento identidade, isto é, para todo a, b, c em R, vale o seguinte:
- (a + b) + c = a + (b + c) (+ é associativa)
- 0 + a = a (0 é a identidade)
- a + b = b + a (+ é comutativa)
- para cada a em R existe −a em R tal que a + (−a) = (−a) + a = 0 (−a é o elemento inverso de a)
- (R, ·) é um monóide com elemento identidade 1, isto é, para todo a, b, c em R, vale:
- (a · b) · c = a · (b · c) (· é associativa)
- 1 · a = a · 1 = a (1 é a identidade)
- Multiplicação se distribui em relação a adição:
- a · (b + c) = (a · b) + (a · c)
- (a + b) · c = (a · c) + (b · c).
- (R, +) é um grupo abeliano com elemento identidade, isto é, para todo a, b, c em R, vale o seguinte:
Exemplos[editar | editar código-fonte]
As próximas tabelas são as tabuadas das operações de adição e multiplicação no anel . Note que este é um número composto, e que (por esse motivo) existem elementos não nulos em cujo produto é zero (no caso, ).
0 1 2 3 4 5 0 0 1 2 3 4 5 1 1 2 3 4 5 0 2 2 3 4 5 0 1 3 3 4 5 0 1 2 4 4 5 0 1 2 3 5 5 0 1 2 3 4
0 1 2 3 4 5 0 0 0 0 0 0 0 1 0 1 2 3 4 5 2 0 2 4 0 2 4 3 0 3 0 3 0 3 4 0 4 2 0 4 2 5 0 5 4 3 2 1
Outro fato curioso que pode ser identificado em alguns anéis é a presença de elementos nilpotentes, ou seja, tais que alguma de suas potências é nula. Por exemplo, em , tem-se .
Veja a tábua de multiplicação completa para o anel de inteiros módulo :
0 1 2 3 4 5 6 7 8 9 10 11 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 2 3 4 5 6 7 8 9 10 11 2 0 2 4 6 8 10 0 2 4 6 8 10 3 0 3 6 9 0 3 6 9 0 3 6 9 4 0 4 8 0 4 8 0 4 8 0 4 8 5 0 5 10 3 8 1 6 11 4 9 2 7 6 0 6 0 6 0 6 0 6 0 6 0 6 7 0 7 2 9 4 11 6 1 8 3 10 5 8 0 8 4 0 8 4 0 8 4 0 8 4 9 0 9 6 3 0 9 6 3 0 9 6 3 10 0 10 8 6 4 2 0 10 8 6 4 2 11 0 11 10 9 8 7 6 5 4 3 2 1
O próximo passo é tentar compreender algebricamente os conjuntos .
| Este módulo tem a seguinte tarefa pendente: Revisar/reescrever/excluir o trecho a seguir (até onde diz "Corolário da p7"). |
No próximo diagrama pode ser observada a estrutura aditiva de :
é subgrupo aditivo de .
, subgrupo aditivo de
- . Logo
Menor tal que .
- gera , ou seja são os blocos básicos.
Observe a seguinte tabela, onde constam as ordens aditivas módulo 6.
1 2 3 4 5 6 0 0 1 1 2 3 4 5 0 2 2 4 0 3 3 0 4 4 2 0 5 5 4 3 2 1 0
- . Logo
Corolário da p7
- Se p é primo então não tem subgrupos triviais.
- ou . Isso implica que ou , donde é domínio de integridade e portanto, é corpo (todo domínio finito é corpo).
Exemplo:
0 1 2 3 4 0 0 0 0 0 0 1 0 1 2 3 4 2 0 2 4 1 3 3 0 3 1 4 2 4 0 4 3 2 1
Outra consequencia é que, fixado z não nulo em Z_p, a função , definida por é injetiva, pois se , ou seja, , então . Como , pode-se concluir que , ou seja, .
Em particular, da sobrejetividade de , e de (a imagem de ), segue a existência de tal que , ou seja, tal que .
Algebricamente, o significado da sobrejetividade de é a existência de um elemento inverso para cada (quando p é primo). No entanto, a argumentação anterior é não construtiva, pois não indica um método para obter o inverso de um certo .
Pode-se obter outra justificativa para a existência de elementos inversos em usando o teorema de Bezout. De fato, se, e somente se, , ou seja, se, e somente, . Usando o algoritmo de Euclides, pode-se então encontrar tais que . Em particular, usando congruências módulo p segue . Donde , ou seja, . Portanto, o procurado é simplesmente .
Resumindo[editar | editar código-fonte]
Os fatos mais relevantes apresentados na discussão feita até agora podem ser sintetizados da seguinte forma:
- Para qualquer , tem-se um anel finito ;
- São equivalentes:
- é corpo;
- é um domínio;
- é um número primo;
- (propriedades algébricas dos conjuntos -- anéis regulares --correspondem a propriedades aritméticas dos numeros inteiros ).
- São também equivalentes:
- tem divisores de zero;
- é um número composto;
Unidades[editar | editar código-fonte]
Para um inteiro arbitrário (seja ele primo ou não), podem ser considerada a questão:
- Quais elementos de são inversíveis?
Antes de responder essa pergunta, convém introduzir uma notação específica para denotar o conjunto dos elementos que possuem inverso multiplicativo:
- Definição
Um elemento de é chamado de unidade quando possui inverso multiplicativo. O conjunto das unidades de denota-se por .
Exemplos[editar | editar código-fonte]
- Se p é número primo, então
Propriedades das unidades[editar | editar código-fonte]
Pode-se verificar que para qualquer , o conjunto , das unidades de , é um grupo multiplicativo finito. Em particular, sempre que , tem-se . Além disso, e existe tal que .
Novamente, a estrutura de reflete as propriedades aritméticas de . Para melhor entender o que isso significa, é interessante saber para cada a quantidade de elementos de . É razoável esperar que esse número varie com , então o melhor é definir uma função que associa com a cardinalidade de :
- Definição
A função de Euler é a função que associa a cada o número de elementos de :
- Observações
- Convenciona-se que .
- O valor é justamente a quantidade de números de a que são coprimos com :
| Demonstração |
|---|
| De fato, se , então existe tal que , ou seja, . Isso significa que , ou seja, que . Segue que .
Reciprocamente, se , então (teorema de Bézout). Logo, e consequentemente, . Neste caso, . |
Exemplos[editar | editar código-fonte]
- Quando é um número primo, tem-se .
- Por outro lado, para números compostos, pode ser bem menor do que . Em particular, .
Curiosidades[editar | editar código-fonte]
O valor de é justamente a quantidade de frações próprias não negativas com denominador (ou seja, ) que já estão na forma irredutível.
Exemplo[editar | editar código-fonte]
No caso apresentado anteriormente, temos as seguintes frações próprias com tal denominador:
Escrevendo cada uma delas na forma irredutível obtém-se:
Pode-se então conferir que, como era esperado, só duas das frações já estavam em sua forma irredutível: e .
Note que ao escrever cada fração em sua forma irredutível os denominadores que surgem são todos divisores de . Além disso, tem-se:
- 1 fração com denominador 1
- 1 fração com denominador 2
- 2 fração com denominador 3
- 2 fração com denominador 6
Totalizando frações. Por outro lado, a seguinte tabela indica um fato muito interessante:
d Número de frações com denominador d 1 1 1 2 1 1 3 2 2 6 2 2
Percebe-se que as duas últimas colunas coincidem. Mas o que isso significa?
Isso quer dizer que o número é, na verdade, igual a soma dos valores de cada um dos divisores . Em símbolos:
Pode-se verificar que essas duas propriedades são válidas em geral:
- é igual à quantidade de frações próprias não negativas com denominador que estão na forma irredutível.
| Justificativa |
|---|
| Fica a cargo do leitor justificar este fato. Sinta-se livre para melhorar a qualidade deste texto, incluindo a justificativa neste módulo. |
Equações lineares[editar | editar código-fonte]
Uma questão muito natural é investigar em que casos há alguma solução para equações lineares do tipo
Exemplo de equação linear com apenas uma solução[editar | editar código-fonte]
Considere em a seguinte equação:
ou, em termos de congruências,
Sabendo que , é possível determinar tais que
Por exemplo, pode-se tomar e . Outra possibilidade é e . Neste caso, nota-se que:
ou seja,
significando que em , ou seja, que neste anel o inverso multiplicativo de é ele mesmo. Sabendo disso, é possível resolver
de forma análoga à utilizada em : Multiplicando-se ambos os membros pelo inverso de , segue:
ou seja,
Conclui-se então que, nesse exemplo, há uma somente uma solução em para a equação dada. Observe ainda que o número não teve qualquer influência no número de soluções para o problema. Isso pode ser percebido considerando para cada o resultado de sua multiplicação por :
0 1 2 3 4 5 6 7 0 3 6 1 4 7 2 5
Note que se tem uma permutação dos elementos de e que, portanto, o único elemento que é levado em ao ser multiplicado por é o . Essa unicidade permaneceria se o fosse trocado por qualquer outro elemento.
Exemplo de equação linear sem solução[editar | editar código-fonte]
Considere a seguinte equação em :
que em termos de congruências se escreve como
Já foi mostrado que ela é equivalente à seguinte equação em :
ou seja,
É claro que tal equação não admite sequer uma solução inteira, uma vez que à esquerda tem-se um número par e a direita um ímpar, ou para ser mais exato, pois .
Exemplo de equação linear com duas soluções[editar | editar código-fonte]
Como um último exemplo antes de conhecer o teorema que dá uma resposta definitiva sobre o número de soluções de uma equação linear em , considere em a equação:
ou seja,
O problema de encontrar soluções para esta equação é equivalente a encontrar inteiros tais que:
Dividindo ambos os membros por dois, obtem-se
ou seja,
Em termos de congruências, segue:
Os números inteiros que verificam essa congruência são os termos da progressão aritmética:
No entanto, como as soluções são buscadas em , devemos considerar os números acima módulo :
ou seja, o conjunto das soluções é:
Em suma, verificou-se através dos exemplos anteriores que é possível encontrar em equações do tipo que possuam uma ou duas soluções, e mesmo equações que não adimitem solução. Essa é uma notavel diferença entre corpos (como , e ) e anéis. Por exemplo, em ou você deve estar habituado a resolver , simplesmente dividindo os dois membros por (e talvez descrevendo esse procedimento como "passar o para o lado direito, dividindo..."). No entanto, é tempo de notar que isso só é possível quando possui inverso. Em , todo número não nulo possui inverso. Mas isso não é verdade em todo anel! Por essa razão torna-se necessário tomar algum cuidado ao resolver equações nos aneis . Fique atento!
Exercícios[editar | editar código-fonte]
- Mostre que, se e é um polinômio com coeficientes inteiros, então .
- Que propriedade aritmética do número inteiro corresponde a existência de elementos nilpotentes em ? (Lembre-se, um elemento é nilpotente quando alguma de suas potências inteiras é igual a zero)






























































![{\displaystyle [a]_{m}=\{x\in \mathbb {Z} ;x\equiv a\!\!\!\!{\pmod {m}}\}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb0baaf8eb33dc005347bcc34bd0980de7f78e33)
![{\displaystyle [a]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ea82bc70a8e322f13a3c4e5b9d5d69e8ef097ad8)
![{\displaystyle [a]_{m}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/54d89656467018df3c7644d8776a28eef1b154c5)

![{\displaystyle \mathbb {Z} /_{\equiv \!\!\!\!{\pmod {m}}}=\{[a]_{m};a\in \mathbb {Z} \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/45299212cbe035716af6931e4b536ae7c8be09f9)





![{\displaystyle [a],[b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9aacc3bd6224ba6355ffc791ed1f41e25202ced4)
![{\displaystyle [a]+[b]=[a+b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c5977b98e7a0ab563b4b4f339caa0ec9dab5b14)
![{\displaystyle [a]\times [b]=[a\times b]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/59759b3bb57c3982f4d03cd1142272307d0f10c3)
![{\displaystyle [a][b]=[ab]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/709d523ac678f932a75edb3c135db415a516eb13)

![{\displaystyle A=[a]=[a']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3360680eed8a4f7e08d95e79a42816a4543a85bc)
![{\displaystyle B=[b]=[b']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/98654edaad6999f6c49cb015dae57378f4ecbdd6)
![{\displaystyle [A]+[B]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f2e02bbc65a58189db9d009b692c5ee712807f4)
![{\displaystyle [a+b],[a'+b],[a+b']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b695b22f3265aef2a4741c83745ffa6717c6c1c)
![{\displaystyle [a'+b']}](https://wikimedia.org/api/rest_v1/media/math/render/svg/77bf37ca8b5433087b1437509fc5c1de80342e2b)




![{\displaystyle \rho (x)=[x]=[x\!\!\!\!{\pmod {m}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4dcf9468bf75be2f36e374095eedef564d637f46)







































































































































