Matemática elementar/Função composta
A avaliação de expressões matemáticas do tipo , e envolvem a aplicação sucessiva de várias funções. Por exemplo, para calcular , quando (x é o ângulo de 45 graus) devemos primeiro calcular e, depois, elevar o resultado ao quadrado.
O nome deste tipo de cálculo de funções em sequência é a composição de funções.
Ou seja, quando se calcula uma expressão da forma g(f(x)), em que f e g são funções, estamos calculando h(x), em que h é a função composta de g e f.
Uma função f(x) deve ser pensada como uma operação que começa no x, depois passa pela função f, gerando o resultado f(x). Uma notação mais adequada para esta imagem visual seria escrever (x)f, mas, infelizmente, a notação historicamente consagrada é f(x).
Assim, a função composta g o f deve ser entendida como uma função h em que, primeiro, a função f é executada, e, em seguida, a função g é executada.
Ou seja, se h = g o f, então temos:
- h(x) = (g o f)(x) = g(f(x))
Conceito[editar | editar código-fonte]
No sentido mais rigoroso, a função composta de duas funções está definida apenas na seguinte situação:
Sejam f e g as duas funções de domínio e contra-domínio:
Então a função composta g o f é a função:
definida por:
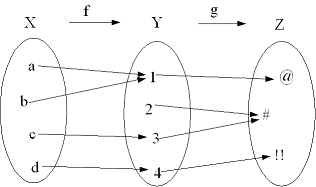
Isto é ilustrado na figura abaixo:
Exemplo[editar | editar código-fonte]
- Para se calcular g o f, devemos pegar a expressão de g(x) e trocar x por f(x). Assim, sendo as funções reais:
temos que:
ou seja:
Problemas de composição de função[editar | editar código-fonte]
Por um abuso de linguagem, usa-se o termo função composta para a situação em que:
Neste caso, g o f é definida apenas para os pontos do domínio de f cuja imagem f(x) pertença também ao domínio de g.
Exemplo[editar | editar código-fonte]
Seja:
Neste caso, como não são dados nem o domínio nem o contra-domínio das funções, supõe-se que o contra-domínio é o conjunto dos números reais, e o domínio é o maior possível.
Ou seja:
Note-se que a função g o f não pode ser avaliada no ponto x = 4 do domínio de f (porque f(4) = 2, e g(2) não está definido nos reais). Assim, para se calcular o domínio de g o f, é necessário forçar que f(x) pertença ao domínio de g, ou seja:
Resolvendo, temos as duas condições:
- - condição para
- - condição para
Ou seja:
Finalmente:
Ou seja, o domínio de g o f é o intervalo fechado [0, 1].
Associatividade[editar | editar código-fonte]
Pode-se estender a definição para a composição de três ou mais funções, de maneira análoga. Sejam
Como o contra-domínio de f é o domínio de g, a função composta g o f está definida:
Analogamente, a função composta h o g também está definida:
De novo, como o contra-domínio de g o f é o domínio de h, podemos construir a função composta h o (g o f):
Finalmente, como o contra-domínio de f é o domínio de h o g, podemos construir a função composta (h o g) o f:
Teorema Nas condições acima, (associatividade)
Prova A prova usa, recursivamente, relações do tipo (g o f)(x) = g(f(x)) - a definição da fórmula da função composta. Esta relação vale para todo x no domínio de f (que é o domínio tanto de (h o g) o f quanto h o (g o f)).
Seja .
Então:
- - pela definição de g o f
- - pela definição de (h o g) o f
- - pela definição de h o (g o f)
Seja y = f(x). Então , então vale também a relação:
- - pela definição de h o g.
Portanto:
Como a relação acima vale para todo x, temos que:
- .
Notação A função composta de três funções pode ser escrita sem os parêntesis:
Explicitamente:
Propriedades[editar | editar código-fonte]
- Se g é a função inversa de f, então a função composta g o f é a identidade no domínio de f, ou seja, g o f(x) = x para todo x no domínio de f
- Se g é a função inversa de f, então a função composta f o g é a identidade no contra-domínio de f, ou seja, f o g(y) = y para todo y no contra-domínio de g
Ver também[editar | editar código-fonte]
Artigo na wikipedia:


















![{\displaystyle g:\ ]-\infty ,1]\rightarrow \mathbb {R} \,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/abfcfb2d0f1bba38b6b8292226794f8ba7a3360d)























