Bioquímica/Cinética enzimática

Cinética enzimática

O estudo da função de enzimas envolve uma aproximação multidisciplinar. Por um lado, a determinação da estrutura, usando técnicas espectroscópicas como a difração de raios-X em proteínas cristalizadas ou a ressonância magnética nuclear (RMN) em proteínas em solução, permite localizar a posição dos diferentes resíduos no espaço. Este tipo de estudo revela muitas vezes detalhes sobre o mecanismo da reação, ou seja, a forma e sequência de ligações do substrato ao centro ativo para ser catalisado. Por outro lado, é importante conhecer parâmetros cinéticos, como a velocidade da reação catalisada, o efeito de inibidores nessa velocidade, quantas moléculas a enzima consegue catalisar por segundo, etc, para poder ser aferida a eficiência dessa enzima e a forma como é regulada.

Esta última aproximação ao estudo de enzimas, a cinética enzimática, é um dos campos de estudo mais clássicos da Bioquímica. Nenhum estudo sobre uma enzima se encontra completo sem estudos cinéticos.

Progressão da reação

Para que uma reação enzimática se dê, a enzima (E) e o substrato (S) têm de se encontrar e formar o complexo enzima-substrato (ES). Como referido anteriormente, embora este possa parecer um formalismo, a formação deste complexo é uma peça chave na compreensão da progressão de uma catálise. O complexo ES é lábil: a enzima pode dissociar-se do seu substrato sem ter havido reação. Este equilíbrio é expresso sob a forma:

E+S $\leftrightarrows$ ES

A enzima pode então transformar o substrato num produto (P). Existe de forma transiente um complexo EP, havendo então dissociação deste complexo em enzima livre (E) e produto (P). Este mecanismo pode escrever-se na forma simplificada:

E+S$\leftrightarrows$[ES]$\rightarrow$E+P

A reação de formação de ES é normalmente mais rápida que a reação de dissociação de EP, ou seja, a libertação do produto da reação é normalmente um passo limitante da reação.

Velocidade inicial

O estudo de uma reação enzimática in vitro não reflete a verdadeira situação das enzimas em células, mas possibilita a simplificação da determinação de parâmetros cinéticos. Dentro de uma célula, o substrato pode estar confinado a um dado compartimento e não sofrer facilmente difusão: por exemplo, pode ser o produto de uma reação anterior numa via metabólica, pelo que passa diretamente de uma enzima para a outra. Normalmente, os estudos in vitro usam uma concentração de substrato muito superior à concentração de enzima, para que a probabilidade de uma enzima encontrar uma molécula de substrato seja o mais elevada possível.

Representação da variação da velocidade inicial da reação (V) em função da concentração de substrato ([S]).

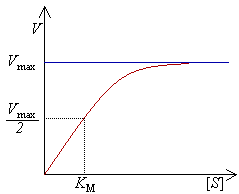
Outra vantagem do uso de uma concentração de substrato ([S]) maior que a concentração de enzima ([E]) é a possibilidade de monitorizar a variação da velocidade de reação com [E] sem que haja uma variação apreciável de [S]. Como S está a ser convertido em P, [S] decresce com o tempo, à medida que o produto se acumula em solução. Como a [S] influencia a formação do complexo ES (e portanto da formação de produto), vai influenciar também a velocidade da reação. No entanto, se for feita apenas a monitorização da velocidade inicial da reação (tipicamente, durante os primeiros 30 a 60 segundos), a variação de [S] não é significativa e pode ser tomada como constante.

Nestas condições, a velocidade medida (velocidade inicial, V₀) depende apenas de [E]. Um gráfico de V₀ em função de [S] apresenta uma forma característica de semi-hipérbole: a baixas concentrações de substrato, a variação de V₀ com [S] é linear; à medida que se usam [S] mais elevadas, V₀ sofre uma variação cada vez menor, tendendo para um valor limite. Este valor é denominado velocidade máxima, V_max.

A que se deve este comportamento? A baixas concentrações de substrato, a maior parte da enzima em solução encontra-se na forma livre, E; usando concentrações suficientemente elevadas de S, toda a enzima se encontrará, num dado instante, em complexo com molécula(s) de substrato, isto é, na forma ES. Por maior que seja a concentração de substrato utilizada, as moléculas de enzima não têm capacidade de catalisar o substrato, por todos os centros ativos se encontrarem ocupados. Nestas condições, diz-se que a enzima se encontra saturada.

Equação de Michaelis-Menten

A semi-hipérbole correspondente ao comportamento da velocidade de uma enzima em função da concentração do substrato pode ser descrita matematicamente pela equação de Michaelis-Menten:

$V_{0}={\frac {V_{max}[S]}{K_{M}+[S]}}$

em que [S], V₀ e V_max são as grandezas anteriormente definidas e K_M a constante de Michaelis. Esta equação pode ser deduzida de forma intuitiva considerando a forma como se desenrola a catálise enzimática.

É assumida, nesta dedução, a existência de um estado estacionário, em que [ES] permanece constante ao longo do tempo. A teoria do estado estacionário, introduzida por G. E. Briggs e J. B. S. Haldane em 1925, considera que a velocidade a que o complexo ES se forma é aproximadamente igual à velocidade da sua dissociação. Existe um curto período de tempo, normalmente na ordem dos microssegundos, em que há uma acumulação de ES – estado pré-estacionário. O estudo da cinética enzimática envolvendo a teoria do estado estacionário é referida como cinética do estado estacionário.

Também é assumido que a concentração de produto é negligível no início da reação, logo é negligível a extensão da reação inversa no equilíbrio entre substrato e produto, S $\leftrightarrows$ P, considerando-se apenas a reação direta na dedução da equação. Assim, a reação é descrita por

E+S $\leftrightarrows$ [ES] $\rightarrow$ E+P

Como já referido, a formação de [ES] limita a velocidade da reação, medida como V₀:

V₀=k₂[ES]

Se [ES] fosse facilmente mensurável, o valor de k₂ seria simples de determinar diretamente. No entanto, esse não é o caso, e o valor de [ES] tem de ser deduzido. Para tal, considere-se que a concentração do total de enzima presente na reação, [E]_t, é o somatório da concentração de enzima em complexo com o substrato, [ES], e da concentração de enzima "livre" (não ligada a substrato), [E]_l:

[E]_t = [E]_l + [ES]

Tratamento matemático e gráfico da equação de Michaelis-Menten

Embora o gráfico obtido diretamente da equação de Michaelis-Menten seja de interpretação relativamente simples, existem tratamentos matemáticos que simplificam a representação gráfica da equação e permitem a obtenção rápida de parâmetros cinéticos.

O tratamento mais conhecido e porventura mais utilizado é o de Lineweaver-Burk. A equação de Michaelis-Menten pode ser transformada numa equação da reta, do tipo y=ax+b:

$V_{o}={\frac {V_{m}ax[S]}{K_{M}+[S]}}\Leftrightarrow {\frac {1}{V_{o}}}={\frac {K_{M}+[S]}{V_{m}ax[S]}}\Leftrightarrow {\frac {1}{V_{o}}}={\frac {K_{M}}{V_{m}ax[S]}}+{\frac {[S]}{V_{m}ax[S]}}\Leftrightarrow {\frac {1}{V_{o}}}={\frac {K_{M}}{V_{m}ax[S]}}+{\frac {1}{V_{m}ax}}$

Gráfico de Lineweaver-Burk.

Esta última forma da equação de Michaelis-Menten é conhecida como equação de Lineweaver-Burk. Um gráfico de ${\frac {1}{V_{o}}}$ (y) em função de ${\frac {1}{[S]}}$ (x) é uma reta de declive igual a ${\frac {K_{M}}{V_{m}ax}}$ (a), que intercepta o eixo das coordenadas na origem no ponto ${\frac {1}{V_{m}ax}}$ (b), interceptando também o eixo das abcissas no ponto ${\frac {-1}{K_{M}}}.$ Este gráfico é também chamado duplo recíproco pois trata-se de uma representação gráfica do recíproco de ambos os parâmetros V_o e [S].

Este tipo de tratamento matemático permite uma determinação mais precisa de V_max, um parâmetro que só se obtém por aproximação num gráfico de Michaelis-Menten.

Outra vantagem na utilização da equação de Lineweaver-Burk é visível em estudos de inibição enzimática, sendo relativamente simples de detectar e distinguir entre diferentes tipos de inibição: ao usar diferentes concentrações de inibidores, e consoante o tipo de inibição efetuada, o gráfico de Lineweaver-Burk muda de uma forma bem estudada, como será mais claro no capítulo sobre inibição enzimática.

• Commons